
Lägsta kostnad metodegenskaper, fördelar, nackdelar

De lägsta kostnad metoden är ett förfarande som används för att erhålla den första möjliga lösningen för ett transportproblem. Används när prioriteringen är att sänka produktdistributionskostnaderna.
Metoden med lägsta kostnad syftar till att uppnå de lägsta transportkostnaderna mellan flera efterfrågecentra (destinationerna) och flera leveranscentra (källorna)..

Produktions- eller leveranskapaciteten för varje källa, liksom kraven eller efterfrågan för varje destination är kända och fasta..
Kostnaden för att transportera en enhet av produkten från varje källa till varje destination är också känd..
Produkten måste transporteras från olika källor till olika destinationer på ett sådant sätt att den tillgodoser efterfrågan från varje destination och samtidigt minimerar den totala transportkostnaden..
Andra metoder kan användas om prioriteten är tidsbesparingar snarare än kostnadsbesparingar.
Artikelindex
- 1 Funktioner
- 1.1 Steg för den billigaste metoden
- 1.2 Tillämpningar
- 2 Fördelar
- 3 Nackdelar
- 4 Exempel
- 4.1 Förklaring av metoden
- 5 Referenser
Egenskaper
Den optimala fördelningen av en produkt från olika källor till olika destinationer kallas ett transportproblem..
- Transportmodeller handlar om transport av en produkt tillverkad i olika fabriker eller fabriker (leveranskällor) till olika lager (efterfrågan).
- Målet är att uppfylla kraven på destinationerna inom anläggningens produktionskapacitetsbegränsningar till lägsta transportkostnad..
Steg för den billigaste metoden
Steg 1
Den cell som innehåller lägsta transportkostnad i hela tabellen väljs. Den cellen tilldelas så många enheter som möjligt. Denna kvantitet kan begränsas av utbud och efterfrågan..
I händelse av att flera celler har den lägsta kostnaden, väljs den cell där maximal tilldelning kan göras.
Sedan fortsätter vi med att justera utbud och efterfrågan i den berörda raden och kolumnen. Den justeras genom att subtrahera det belopp som tilldelats cellen.
Steg 2
Raden eller kolumnen där utbudet eller efterfrågan har förbrukats (oavsett om det är noll) elimineras.
Om båda värdena, utbudet och efterfrågan är lika med noll, kan valfri rad eller kolumn elimineras, godtyckligt.
Steg 3
De tidigare stegen upprepas med nästa lägsta kostnad och fortsätter tills allt tillgängligt utbud i de olika källorna eller hela efterfrågan från de olika destinationerna är uppfyllt..
Applikationer
- Minimera transportkostnaderna från fabriker till lager eller från lager till butiker.
- Bestäm den lägsta kostnaden för en ny fabrik, lager eller försäljningskontor.
- Bestäm produktionsprogrammet för minimikostnader som uppfyller företagets efterfrågan med produktionsbegränsningar.
Fördel
Den billigaste metoden anses ge mer exakta och optimala resultat jämfört med det nordvästra hörnet.
Detta beror på att nordvästra hörnmetoden bara tar hänsyn till utbuds- och tillgänglighetsbehovet, med det övre vänstra hörnet som ursprunglig ersättning, oavsett fraktkostnad..
Å andra sidan inkluderar minimikostnadsmetoden transportkostnader medan uppdrag görs..
- Till skillnad från nordvästra hörnmetoden ger den här metoden en exakt lösning eftersom den tar hänsyn till transportkostnaden vid kartläggning.
- Den billigaste metoden är en mycket enkel metod att använda.
- Det är väldigt enkelt och lätt att beräkna den optimala lösningen med denna metod.
- Den billigaste metoden är mycket lätt att förstå.
Nackdelar
- För att få den optimala lösningen måste vissa regler följas. Dock följer de lägsta kostnaderna inte steg för steg.
- Metoden med lägsta kostnad följer inga systematiska regler när det är oavgjort i den lägsta kostnaden.
- Den billigaste metoden möjliggör val genom personalobservation, vilket kan skapa missförstånd för att få den optimala lösningen.
- Den har inte förmågan att tillhandahålla någon form av kriterier för att avgöra om den lösning som erhålls med den här metoden är den mest optimala..
- Antalet erbjudanden och krav är alltid desamma eftersom de inte varierar över tiden..
- Det tar inte hänsyn till andra typer av faktorer att tilldela, utan bara transportkostnaderna.
Exempel
Begreppet metoden för lägsta kostnad kan förstås genom följande problem:
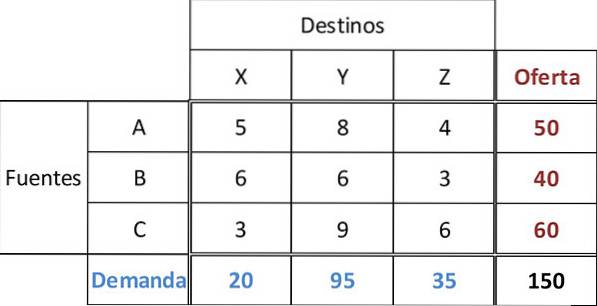
I denna tabell är tillförseln för varje källa A, B, C 50, 40 respektive 60 enheter. Efterfrågan från de tre återförsäljarna X, Y, Z är 20, 95 respektive 35 enheter. För alla rutter anges transportkostnaden.
Lägsta transportkostnad kan erhållas genom att följa stegen nedan:
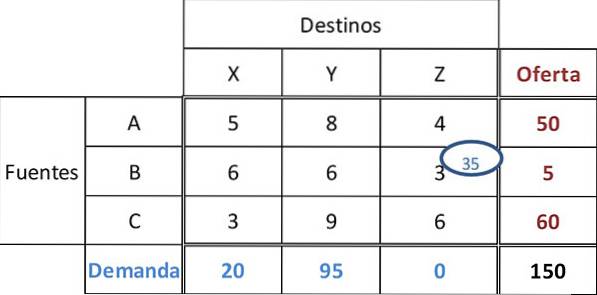
Lägsta kostnad i tabellen är 3, med oavgjort i cellerna BZ och CX. Generellt, för att få den bästa initiala lösningen, bör kostnaden väljas där det största beloppet kan fördelas.
Därför tilldelas 35 enheter till cell BZ. Detta tillgodoser efterfrågan från återförsäljaren Z och lämnar 5 enheter i källa B.
Förklaring av metoden
Återigen är minimikostnaden 3. Därför kommer 20 enheter att tilldelas cell CX. Detta tillgodoser efterfrågan från återförsäljaren X och lämnar 40 enheter i källa C.
Nästa minimikostnad är 4. Efterfrågan på Z är dock redan klar. Vi går till nästa minimikostnad, som är 5. Även efterfrågan på X har redan slutförts.
Nästa minimikostnad är 6, med oavgjort mellan tre celler. Du kan dock inte tilldela enheter till cellerna BX och CZ, eftersom efterfrågan från återförsäljarna X och Z är uppfyllt. Sedan tilldelas 5 enheter till cell BY. Detta slutför leveransen av källa B.
Nästa minimikostnad är 8, att tilldela 50 enheter till cell AY och slutföra leveransen från källa A.
Nästa minimikostnad är 9. 40 enheter tilldelas cell CY, och därmed kompletteras efterfrågan och utbudet för alla destinationer och källor. Det slutliga slutuppdraget är:
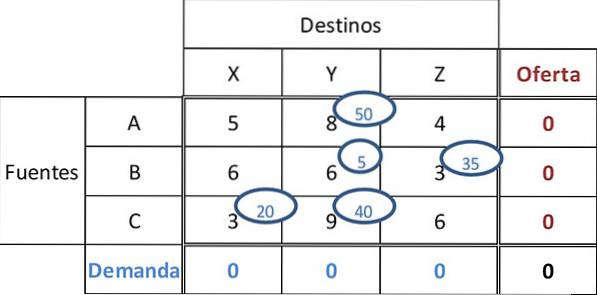
Den totala kostnaden kan beräknas genom att multiplicera de tilldelade beloppen med kostnaderna i motsvarande celler: Total kostnad = 50 * 8 + 5 * 6 + 35 * 3 + 20 * 3 + 40 * 9 = 955.
Referenser
- Affärsjargoner (2019). Lägsta kostnadsmetoden. Hämtad från: businessjargons.com.
- Uppdragsrådgivning (2019). Hjälp för tilldelning av lägsta kostnadsmetod. Hämtad från: assignmentconsultancy.com.
- Affärsledning (2015). Transportproblem. Hämtad från: engineering-bachelors-degree.com.
- Josefina Pacheco (2019). Vad är metoden för lägsta kostnad? Webb och företag. Hämtad från: webyempresas.com.
- Atozmath (2019). Exempel på lägsta kostnadsmetod. Hämtad från: cbom.atozmath.com.


Ingen har kommenterat den här artikeln än.