
Hur man beräknar molär absorptionsförmåga och lösta övningar
De molär absorptionsförmåga det är en kemisk egenskap som indikerar hur mycket ljus en art kan absorbera i lösning. Detta koncept är mycket viktigt inom den spektroskopiska analysen av absorption av fotonstrålning med energier i det ultravioletta och synliga området (UV-vis)..
Eftersom ljus består av fotoner med sina egna energier (eller våglängder), beroende på vilken art eller blandning som analyseras, kan en foton absorberas i större grad än en annan; det vill säga ljus absorberas vid vissa våglängder som är karakteristiska för ämnet.

Således är värdet av molär absorptionsförmåga direkt proportionellt mot graden av ljusabsorption vid en given våglängd. Om arten absorberar lite rött ljus kommer dess absorptionsvärde att vara lågt; medan det finns en uttalad absorption av rött ljus kommer absorberingsförmågan att ha ett högt värde.
En art som absorberar rött ljus kommer att reflektera en grön färg. Om den gröna färgen är mycket intensiv och mörk, betyder det att det finns stark absorption av rött ljus.
Vissa gröna nyanser kan dock bero på reflektioner av olika serier av gula och blues, som blandas och upplevs som turkos, smaragd, glas etc..
Artikelindex
- 1 Vad är molar absorptionsförmåga?
- 1.1 Enheter
- 2 Hur man beräknar det?
- 2.1 Direkt godkännande
- 2.2 Grafmetod
- 3 Lösta övningar
- 3.1 Övning 1
- 3.2 Övning 2
- 4 Referenser
Vad är molar absorptionsförmåga?
Molarabsorptionsförmåga är också känd genom följande beteckningar: specifik extinktion, molär dämpningskoefficient, specifik absorption eller bunsenkoefficient; Det har till och med kommit att namnges på andra sätt, så det har varit en källa till förvirring.
Men vad är exakt molabsorptionsförmåga? Det är en konstant som definieras i det matematiska uttrycket för Lamber-Beer-lagen, och det anger helt enkelt hur mycket den kemiska arten eller blandningen absorberar ljus. En sådan ekvation är:
A = εbc
Där A är absorbans för lösningen vid en vald våglängd λ; b är längden på cellen där provet som ska analyseras finns och därför är avståndet som ljuset passerar i lösningen; c är koncentrationen av den absorberande arten; och ε, den molära absorptionsförmågan.
Med tanke på λ, uttryckt i nanometer, förblir värdet av ε konstant; men när man ändrar värdena på λ, det vill säga när man mäter absorbanser med ljus från andra energier, ändras ε och når antingen ett minimi- eller maximivärde.
Om dess maximala värde är känt, εmax, bestäms samtidigt λmax; det vill säga det ljus som arten absorberar mest:
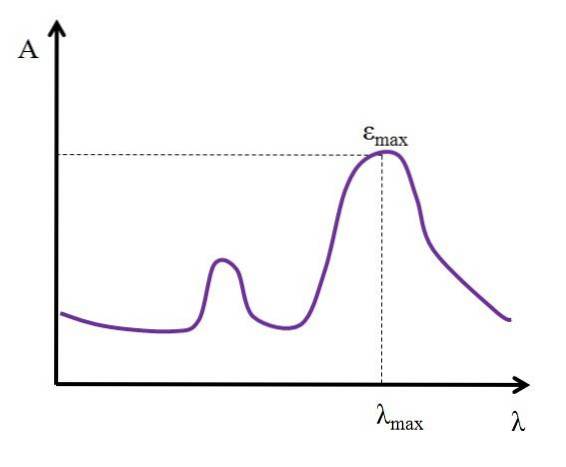
Enheter
Vad är enheterna för ε? För att hitta dem måste det vara känt att absorbanser är måttlösa värden; och därför måste multipliceringen av enheterna b och c avbrytas.
Koncentrationen av den absorberande arten kan uttryckas antingen i g / L eller mol / L, och b uttrycks vanligtvis i cm eller m (eftersom det är längden på cellen som ljusstrålen passerar genom). Molaritet är lika med mol / L, så c uttrycks också som M.
Således multiplicerar vi enheterna b och c: M ∙ cm. Vilka enheter måste då ε ha för att göra värdet på A måttlöst? De som multiplicerar M ∙ cm ger ett värde på 1 (M ∙ cm x U = 1). Lösning för U, vi får helt enkelt M-1∙ cm-1, som också kan skrivas som: L ∙ mol-1∙ cm-1.
Använd faktiskt M-enheterna-1∙ cm-1 eller L ∙ mol-1∙ cm-1 påskynda beräkningar för att bestämma molär absorptionsförmåga. Emellertid uttrycks det ofta också i enheter av mtvå/ mol eller cmtvå/ mol.
När de uttrycks med dessa enheter måste vissa omvandlingsfaktorer användas för att modifiera enheterna b och c.
Hur man beräknar det?
Direkt godkännande
Molarabsorptionsförmåga kan beräknas direkt genom att lösa den i ovanstående ekvation:
ε = A / bc
Om koncentrationen av den absorberande arten, celllängden och absorbansen erhållen vid en våglängd är känd, kan ε beräknas. Men detta sätt att beräkna det ger ett felaktigt och opålitligt värde.
Diagrammetod
Om du tittar noga på Lambert-Beer-lagekvationen, kommer du att märka att den ser ut som ekvationen för en linje (Y = aX + b). Detta innebär att om A-värdena plottas på Y-axeln och de på c på X-axeln, måste en rät linje erhållas som passerar genom ursprunget (0,0). Således skulle A bli Y, X skulle vara c och a skulle vara lika med εb.
När raden väl är ritad räcker det därför att ta två punkter för att bestämma lutningen, det vill säga a. När detta väl är gjort och längden på cellen, b, är känd, är det lätt att lösa värdet på ε.
Till skillnad från direkt clearance, gör graferna A vs c det möjligt att beräkna absorbansmätningarna och reducera experimentfelet. och dessutom kan oändliga linjer passera genom en enda punkt, så direkt spelrum är inte praktiskt.
På samma sätt kan experimentella fel orsaka att en rad inte passerar genom två, tre eller fler punkter, så den linje som erhålls efter tillämpningen av metoden med minsta kvadrat används faktiskt (en funktion som redan är integrerad i miniräknare). Allt detta förutsätter hög linjäritet och följaktligen Lamber-Beer-lagen..
Lösta övningar
Övning 1
Det är känt att en lösning av en organisk förening med en koncentration av 0,008739 M uppvisade en absorbans av 0,6346, mätt vid X = 500 nm och med en celllängd 0,5 cm. Beräkna molens absorptionsförmåga för komplexet vid denna våglängd.
Från dessa data kan ε lösas direkt:
ε = 0,6346 / (0,5 cm) (0,008739M)
145,23 M-1∙ cm-1
Övning 2
Följande absorbanser mäts vid olika koncentrationer av ett metallkomplex vid en våglängd av 460 nm och med en cell på 1 cm i längd:
A: 0,03010 0,1033 0,1584 0,3961 0,8093
c: 1,8 ∙ 10-5 6 ∙ 10-5 9.2 ∙ 10-5 2.3 ∙ 10-4 5.6 ∙ 10-4
Beräkna molens absorptionsförmåga för komplexet.
Det finns totalt fem poäng. För att beräkna ε är det nödvändigt att rita dem genom att placera värdena A på Y-axeln och koncentrationerna c på X-axeln. När detta är gjort bestäms den minsta kvadratlinjen och med dess ekvation kan vi bestämma ε.
I detta fall plottar du punkterna och drar linjen med en bestämningskoefficient Rtvå 0,9905, lutningen är lika med 7 ∙ 10-4; det vill säga εb = 7 ∙ 10-4. Därför, med b = 1 cm, kommer ε att vara 1428,57 M-1.centimeter-1 (1/7 ∙ 10-4).
Referenser
- Wikipedia. (2018). Mol dämpningskoefficient. Återställd från: en.wikipedia.org
- Vetenskap slog. (2018). Molar Absorptivity. Återställd från: sciencestruck.com
- Kolorimetrisk analys: (Beers lag eller spektrofotometrisk analys). Återställd från: chem.ucla.edu
- Kerner N. (s.f.). Experiment II - Lösningsfärg, absorbans och öl. Återställd från: umich.edu
- Day, R., & Underwood, A. Kvantitativ analytisk kemi (femte upplagan). PEARSON Prentice Hall, s-472.
- Gonzáles M. (17 november 2010). Absorptivitet Återställd från: quimica.laguia2000.com



Ingen har kommenterat den här artikeln än.