
Sannolikhetsaxiomtyper, förklaring, exempel, övningar
De axiomer av sannolikhet de är matematiska propositioner som hänvisar till sannolikhetsteorin, som inte förtjänar bevis. Axiomerna grundades 1933 av den ryska matematikern Andrei Kolmogorov (1903-1987) i sitt arbete Grundläggande om sannolikhetsteori och lade grunden för den matematiska studien av sannolikhet.
När du utför ett visst slumpmässigt experiment ξ är provutrymmet E en uppsättning av alla möjliga resultat av experimentet, även kallat evenemang. Varje händelse betecknas som A och P (A) är sannolikheten för dess händelse. Då konstaterade Kolmogorov att:

-Axiom 1 (inte negativitet): sannolikheten för att någon händelse A inträffar är alltid positiv eller noll, P (A) ≥0. När sannolikheten för en händelse är 0 kallas den omöjlig händelse.
-Axiom 2 (säkerhet): när någon händelse som tillhör E, är dess sannolikhet för händelse 1, som vi kan uttrycka som P (E) = 1. Det är det som kallas en säker händelse, eftersom när man genomför ett experiment, med all säkerhet finns det ett resultat.
-Axiom 3 (tillägg): i fallet med två eller flera inkompatibla händelser två och två, kallad A1, TILLtvå, TILL3…, Sannolikheten för att händelse A inträffar1 plus Atvå plus A3 och så vidare är det summan av sannolikheterna att var och en sker separat.
Detta uttrycks som: P (A1 U Atvå U A3 U…) = P (A1) + P (A.två) + P (A.3) + ...

Artikelindex
- 1 Exempel
- 2 sätt att tilldela sannolikhet
- 2.1 Laplaces regel
- 2.2 Relativ frekvens
- 3 Övningen löst
- 3.1 Lösning a
- 4 Referenser
Exempel
Sannolikhetsaxiomerna används ofta i en mängd applikationer. Till exempel:
En häftstift eller hål kastas i luften, och när den faller på golvet finns det möjlighet att landa med spetsen uppåt (U) eller med spetsen nedåt (D) (vi kommer inte att överväga andra möjligheter). Exempelutrymmet för detta experiment består av dessa händelser, sedan E = U, D.

Genom att tillämpa axiomerna har vi:
P (E) = 1 (Axiom 2)
Men P (E) = P (U) + P (D) (Axiom 3), eftersom dessa händelser är ömsesidigt oförenliga eller inte sammanhängande. Häftstiftet faller inte med spetsen uppåt eller nedåt samtidigt, det är det ena eller det andra, men inte båda, eftersom andra möjligheter inte övervägs. Sedan:
P (U) + P (D) = 1
P (U) = 1 - P (D)
Oavsett om det är lika troligt att landa upp eller ner, P (U) = P (D) = ½ (Axiom 1). Det kan dock vara så att konstruktionen och utformningen av häftstiftet är mer benägna att falla på ett eller annat sätt. Det kan till exempel vara så P (U) = ¾ medan P (D) = ¼ (Axiom 1).
Observera att i båda fallen ger summan av sannolikheterna 1. Axiomerna anger dock inte hur sannolikheterna ska tilldelas, åtminstone inte helt. Men de bekräftar att de är siffror mellan 0 och 1 och att summan av alla, som i det här fallet, är 1.
Sätt att tilldela sannolikhet
Sannolikhetsaxiomerna är inte en metod för att tilldela sannolikhetsvärdet. För detta finns det tre alternativ som är kompatibla med axiomerna:
Laplaces regel
Varje händelse tilldelas samma sannolikhet för att hända, då definieras sannolikheten för händelse som:
P (A) = antal fall som är gynnsamma för händelse A / antal möjliga fall
Till exempel, vad är sannolikheten för att dra ett ess från en kortlek med franska kort? Kortet har 52 kort, 13 av varje färg och det finns fyra färger. Varje färg har 1 ess, så totalt finns det 4 ess:
P (som) = 4/52 = 1/13
Laplaces regel är begränsad till begränsade provutrymmen, där varje händelse är lika troligt.
Relativ frekvens
Här måste experimentet vara repeterbart, eftersom metoden bygger på att utföra ett stort antal repetitioner..
Låt oss göra i upprepningar av experimentet ξ, av vilka vi finner att n är antalet gånger som viss händelse A inträffar, då är sannolikheten att denna händelse inträffar:
P (A) = limi → ∞ (varken)
Där n / i är den relativa frekvensen för en händelse.
Definition av P (A) på detta sätt uppfyller Kolmogorovs axiomer, men har nackdelen att många tester måste utföras för att sannolikheten ska vara lämplig.
Subjektiv metod
En person eller en grupp människor kan komma överens om att tilldela sannolikheten för en händelse genom sitt eget omdöme. Denna metod har nackdelen att olika personer kan tilldela olika sannolikheter till samma händelse..
Övningen löst
I experimentet att samtidigt kasta 3 ärliga mynt, få sannolikheten för de beskrivna händelserna:
a) 2 huvuden och en svans.
b) 1 huvud och två svansar
c) 3 korsningar.
d) Minst ett ansikte.
Lösning till
Huvud betecknas med C och svansar av X. Men det finns flera sätt att få två huvuden och en svans. Till exempel kan de första två mynten landa huvuden och det tredje kan landa svansar. Eller så kan det första falla huvuden, det andra svansarna och det tredje huvudet. Och slutligen kan den första vara svansar och de återstående huvuden.
För att svara på frågorna är det nödvändigt att känna till alla möjligheter, som beskrivs i ett verktyg som kallas träddiagram eller sannolikhetens träd:
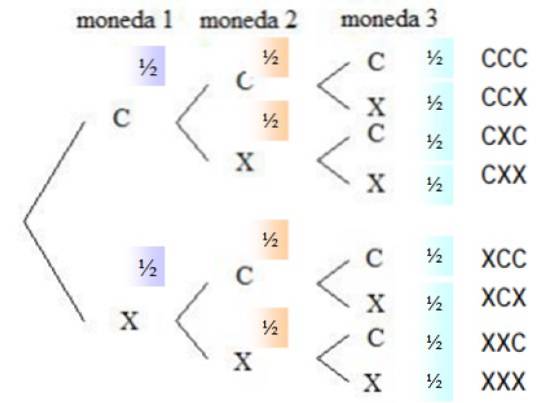
Sannolikheten att något mynt kommer ut ur huvudet är ½, detsamma gäller för svansar, eftersom myntet är ärligt. I den högra kolumnen listas alla möjligheter som kastet har, det vill säga provutrymmet.
Från samplingsutrymmet väljs kombinationerna som svarar på den begärda händelsen, eftersom ordningen i vilken ansiktena inte är viktig. Det finns tre gynnsamma händelser: CCX, CXC och XCC. Sannolikheten för att varje händelse inträffar är:
P (CCX) = ½. ½. ½ = 1/8
Detsamma händer för CXC- och XCC-händelserna, var och en har en 1/8 sannolikhet för att hända. Därför är sannolikheten för att få exakt två huvuden summan av sannolikheten för alla gynnsamma händelser:
P (2-sidig) = 1/8 + 1/8 + 1/8 = 3/8 = 0,375
Lösning b
Att hitta sannolikheten att exakt två korsningar uppstår är ett problem som är analogt med det föregående, det finns också tre gynnsamma händelser som tas från samplingsutrymmet: CXX, XCX och XXC. Därför:
P (2 korsningar) = 3/8 = 0,375
Lösning c
Intuitivt vet vi att sannolikheten för att få 3 svansar (eller 3 huvuden) är lägre. I det här fallet är den eftersträvade händelsen XXX, i slutet av den högra kolumnen, vars sannolikhet är:
P (XXX) = ½. ½. ½ = 1/8 = 0,125.
Lösning d
Det begärs att få minst 1 ansikte, detta innebär att 3 ansikten, 2 ansikten eller 1 ansikte kan komma ut. Den enda händelsen som är oförenlig med detta är den där tre svansar kommer ut, vars sannolikhet är 0,125. Därför är den eftersträvade sannolikheten:
P (minst 1 huvud) = 1 - 0,125 = 0,875.
Referenser
- Canavos, G. 1988. Sannolikhet och statistik: Tillämpningar och metoder. Mcgraw hill.
- Devore, J. 2012. Sannolikhet och statistik för teknik och vetenskap. 8: e. Utgåva. Cengage.
- Lipschutz, S. 1991. Schaum-serien: Sannolikhet. Mcgraw hill.
- Obregón, I. 1989. Teori om sannolikhet. Ledare Limusa.
- Walpole, R. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.


Ingen har kommenterat den här artikeln än.