
Carnot cykelsteg, applikationer, exempel, övningar
De Carnot cykel det är sekvensen av termodynamiska processer som sker i en Carnot-motor, en idealisk enhet som endast består av reversibla processer; de som har ägt rum kan återgå till det ursprungliga tillståndet.
Denna typ av motor anses vara idealisk, eftersom den saknar spridning, friktion eller viskositet som uppstår i verkliga maskiner och omvandlar termisk energi till användbart arbete, även om konverteringen inte utförs 100%.

En motor byggs med utgångspunkt från ett ämne som kan utföra arbete, såsom gas, bensin eller ånga. Detta ämne utsätts för olika temperaturförändringar och upplever i sin tur variationer i dess tryck och volym. På detta sätt är det möjligt att flytta en kolv inuti en cylinder.
Artikelindex
- 1 Vad är carnotcykeln?
- 2 etapper av Carnot-cykeln
- 2.1 Utgångspunkt
- 2.2 Första steget: isotermisk expansion
- 2.3 Andra etappen: adiabatisk expansion
- 2.4 Tredje steget: isotermisk kompression
- 2.5 Fjärde steget: adiabatisk kompression
- 3 Carnots teorem
- 3.1 Bevis på Carnots teorem
- 3.2 Resultat av satsen och begränsningar
- 4 Exempel
- 4.1 En kolv inuti en cylinder
- 4.2 Olika reversibla processer
- 4.3 Ett kärnkraftverk
- 5 Övningar lösta
- 5.1 -Exempel 1: effektivitet hos en värmemotor
- 5.2-Exempel 2: absorberad värme och överförd värme
- 6 Referenser
Vad är carnotcykeln?
Carnot-cykeln äger rum i ett system som kallas Carnot-motorn eller C, som är en idealisk gas innesluten i en cylinder och försedd med en kolv, som är i kontakt med två källor vid olika temperaturer T1 och ttvå som den som visas i bilden nedan till vänster.
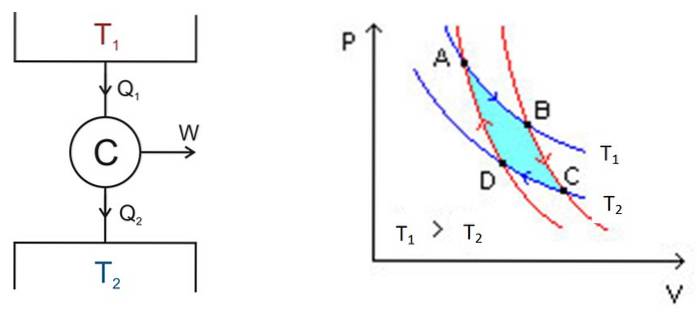
Där sker följande grova processer:
- En viss mängd värme tillförs enheten Qinträde = Q1 från värmetanken vid hög temperatur T1.
- Carnots motor C utför arbete W tack vare denna tillförda värme.
- En del av värmen som används: avfallet Qutgång, överförs till den termiska tanken som har en lägre temperatur Ttvå.
Stadier av Carnot-cykeln
Analysen utförs med hjälp av ett P-V-diagram (tryck-volym), som visas i figur 2 (höger bild). Syftet med motorn kan vara att hålla den termiska behållaren 2 sval och extrahera värme från den. I detta fall är det en kylmaskin. Om du å andra sidan vill överföra värme till termisk tank 1 är det en värmepump.
P-V-diagrammet visar förändringarna i motorns tryck - temperatur under två förhållanden:
- Håll temperaturen konstant (isotermisk process).
- Ingen värmeöverföring (värmeisolering).
De två isotermiska processerna måste anslutas, vilket uppnås genom värmeisolering.
Punkt
Du kan börja när som helst i cykeln, där gasen har vissa tryck-, volym- och temperaturförhållanden. Gasen genomgår en serie processer och kan återgå till startförhållandena för att starta en ny cykel, och den slutliga interna energin är alltid densamma som den initiala. Eftersom energi sparas:
Arbetet utfört med C = Värmeingång - Värmeeffekt
AW = Qinträde - Futgång
Området inom denna slinga, i turkos i figuren, motsvarar exakt det arbete som Carnot-motorn utfört.
I figur 2 markeras punkterna A, B, C och D. Vi börjar vid punkt A efter den blå pilen..
Första steget: isotermisk expansion
Temperaturen mellan punkterna A och B är T1. Systemet absorberar värme från den termiska reservoaren 1 och genomgår en isotermisk expansion. Sedan ökar volymen och trycket minskar.
Emellertid förblir temperaturen vid T1, sedan när gasen expanderar svalnar den. Därför förblir dess inre energi konstant.
Andra etappen: adiabatisk expansion
Vid punkt B börjar systemet en ny expansion där systemet varken vinner eller tappar värme. Detta uppnås genom att placera den i värmeisolering enligt ovan. Därför är det en adiabatisk expansion som fortsätter att peka C efter den röda pilen. Volymen ökar och trycket sjunker till sitt lägsta värde.
Tredje steget: isotermisk kompression
Den börjar vid punkt C och slutar vid D. Isoleringen avlägsnas och systemet kommer i kontakt med värmetanken 2, vars temperatur Ttvå är mindre. Systemet överför spillvärme till den termiska behållaren, trycket börjar öka och volymen att minska.
Fjärde steget: adiabatisk kompression
Vid punkt D går systemet tillbaka till värmeisolering, trycket ökar och volymen minskar tills det når de ursprungliga förhållandena i punkt A. Därefter upprepas cykeln igen..
Carnots sats
Carnot's teorem postulerades först i början av 1800-talet av den franska fysikern Sadi Carnot. 1824 publicerade Carnot, som var en del av den franska armén, en bok där han föreslog svaret på följande fråga: under vilka förhållanden har en värmemotor maximal effektivitet? Carnot fastställde sedan följande:
Ingen värmemotor som går mellan två värmebehållare är effektivare än Carnot-motorn.
Effektiviteten η för en värmemotor ges av kvoten mellan arbetet W och den värmeabsorberade Q:
prestanda = utfört arbete / värmeabsorberat
På detta sätt är effektiviteten för en värmemotor I: η = W / Q. Medan effektiviteten hos en Carnot-motor R är η '= W / Q', förutsatt att båda motorerna kan utföra samma arbete.
Carnots sats säger att η aldrig är större än η '. Annars faller det i strid med termodynamikens andra lag, enligt vilken en process där resultatet är att värme kommer ut från en kropp med lägre temperatur för att gå till en högre temperatur utan att få extern hjälp är omöjlig. Därför:
η < η''
Bevis på Carnots sats
För att visa att detta är så, överväga att Carnot-motorn fungerar som en kylmaskin som drivs av en I-motor. Detta är möjligt eftersom Carnot-motorn fungerar med reversibla processer, som specificerades i början..
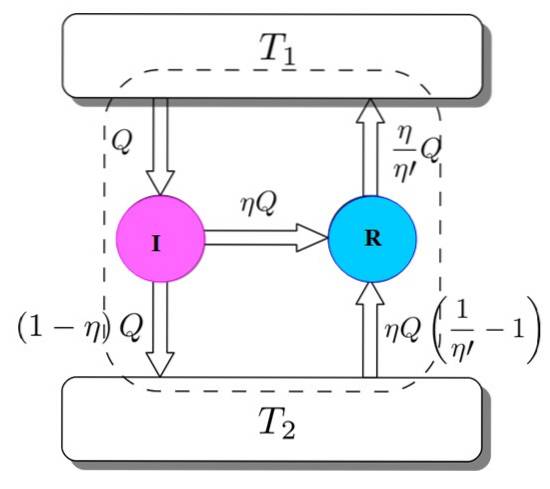
Vi har båda: I och R arbetar med samma termiska reservoarer och det antas att η > η''. Om en motsägelse uppnås med termodynamikens andra lag, bevisas Carnos teorem genom reduktion till absurditet.
Figur 3 hjälper dig att följa processen. Motorn I tar in en mängd värme Q, som den delar upp på detta sätt: utför arbete på R motsvarande W = ηQ och resten är värmen som överförs (1-η) Q till värmebehållaren Ttvå.
Eftersom energi bevaras gäller allt följande:
OCHinträde = Q = Arb W + värme till Ttvå = ηQ + (1-η) Q = Eutgång
Nu tar Carnot kylmaskin R från värmebehållaren 2 en mängd värme som ges av:
(η / η ') (1-η') Q =
Energi måste också sparas i detta fall:
OCHinträde = ηQ + (η / η ') (1-η') Q = (η / η ') Q = Q' = Eutgång
Resultatet är överföringen till värmetanken Ttvå av en värmemängd som ges av (η / η ') Q = Q'.
Om η är större än η 'betyder det att mer värme har nått den termiska avsättningen med högre temperatur än vad jag ursprungligen tog. Eftersom inget externt medel, som en annan värmekälla, har deltagit, är det enda sättet som kan hända att den kallaste termiska reservoaren ger upp värmen..
Detta strider mot termodynamikens andra lag. Då dras slutsatsen att det inte är möjligt att η'' är mindre än η, därför kan motorn I inte ha mer effektivitet än Carnot-maskinen R.
Sats om teorem och begränsningar
Resultatet av Carnots teorem säger att två Carnot-maskiner har samma effektivitet om de båda arbetar med samma termiska reservoarer..
Det betyder oavsett substans, prestationen är oberoende och kan inte höjas genom att ändra den..
Slutsatsen från ovanstående analys är att Carnot-cykeln är den idealiskt uppnåbara toppen av den termodynamiska processen. I praktiken finns det många faktorer som minskar effektiviteten, till exempel det faktum att isoleringen aldrig är perfekt och i de adiabatiska stadierna sker det faktiskt värmeväxling med utsidan.
När det gäller en bil blir motorblocket varmt. Å andra sidan fungerar inte blandningen av bensin och luft exakt som en idealgas, vilket är utgångspunkten för Carnot-cykeln. För att bara nämna några faktorer som kommer att orsaka en drastisk minskning av prestanda.
Exempel
En kolv inuti en cylinder
Om systemet är en kolv innesluten i en cylinder som i figur 4, stiger kolven under isotermisk expansion, vilket kan ses i det första diagrammet längst till vänster, och stiger också under adiabatisk expansion.
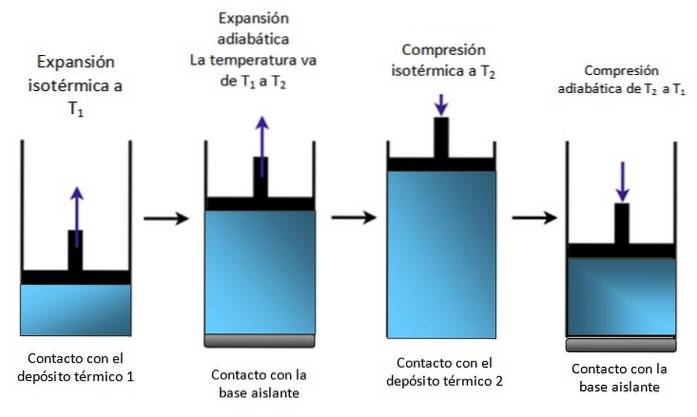
Den komprimeras sedan isotermiskt, ger upp värme och fortsätter att komprimera adiabatiskt. Resultatet är en rörelse där kolven går upp och ner inuti cylindern och som kan överföras till andra delar av en viss anordning, till exempel en bilmotor som producerar vridmoment eller en ångmotor.
Olika reversibla processer
Förutom expansionen och komprimeringen av en idealgas inuti en cylinder finns det andra ideala reversibla processer med vilka en Carnot-cykel kan konfigureras, till exempel:
- Fram och tillbaka rörelser i frånvaro av friktion.
- En idealisk fjäder som komprimerar och dekomprimerar och aldrig deformeras.
- Elektriska kretsar där det inte finns några motstånd för att sprida energi.
- Magnetiserings- och demagnetiseringscykler där det inte finns några förluster.
- Ladda och ladda ur ett batteri.
Ett kärnkraftverk
Även om det är ett mycket komplext system är en första approximation av vad som krävs för att producera energi i en kärnreaktor enligt följande:
- En termisk källa, bestående av ett radioaktivt sönderfallande material såsom uran.
- Den kalla kylflänsen eller behållaren som skulle vara atmosfären.
- "Carnot-motorn" som använder flytande, nästan alltid kranvatten, till vilken värme tillförs från värmekällan för att omvandla den till ånga.
När cykeln genomförs erhålls elektrisk energi som nettoarbete. Vid omvandling till ånga vid hög temperatur får vattnet att nå en turbin där energin omvandlas till rörelse eller kinetisk energi.
Turbinen driver i sin tur en elektrisk generator som omvandlar energin i dess rörelse till elektrisk energi. Förutom klyvbart material som uran kan naturligtvis fossila bränslen användas som värmekälla..
Lösta övningar
-Exempel 1: effektivitet hos en värmemotor
Effektiviteten hos en värmemotor definieras som kvoten mellan utgångsarbetet och insatsarbetet, och därför är det en måttlös mängd:
Maximal effektivitet = (Qinträde - F utgång) / Qinträde
Betecknar maximal effektivitet som emax, det är möjligt att visa sitt beroende av temperatur, vilket är den enklaste variabeln att mäta, såsom:
ochmax = 1 - (Ttvå/ T1)
Där Ttvå är sumptemperaturen och T1 är värmekällans temperatur. Eftersom det senare är större, visar sig effektiviteten alltid vara mindre än 1.
Antag att du har en värmemotor som kan fungera på följande sätt: a) Mellan 200 K och 400 K, b) Mellan 600 K och 400 K. Vad är effektiviteten i varje fall?
Lösning
a) I det första fallet är effektiviteten:
ochmax1 = 1 - (200/400) = 0,50
b) För det andra läget blir effektiviteten:
ochmax2 = 1- (400/600) = 0,33
Även om temperaturskillnaden är densamma mellan båda lägena är effektiviteten inte. Och ännu mer anmärkningsvärt är att det mest effektiva läget fungerar vid en lägre temperatur..
-Exempel 2: absorberad värme och värme frisatt
En 22% effektiv värmemotor ger 1530 J arbete. Hitta: a) Mängden värme som absorberas från värmebehållaren 1, b) Mängden värme som släpps ut till värmebehållaren 2.
a) I det här fallet används definitionen av effektivitet, eftersom arbetet som utförs är tillgängligt, inte temperaturerna i värmetankarna. En effektivitet på 22% innebär att e max = 0,22, därför:
Maximal effektivitet = Arbete / Qinträde
Mängden absorberad värme är exakt Finträde, så clearing har vi:
Finträde = Arbete / effektivitet = 1530 J / 0,22 = 6954,5 J
b) Mängden värme som överförs till den kallaste tanken hittas från ΔW = Qinträde - Futgång
Futgång = Qinträde - ΔW = 6954,5 -1530 J = 5424,5 J.
Ett annat sätt är från ochmax = 1 - (Ttvå/ T1). Eftersom temperaturerna inte är kända, men de är relaterade till värme, kan effektiviteten också uttryckas som:
ochmax = 1 - (Qgav/ Qabsorberad)
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 654-657
- Kärnenergi. Drift av ett kärnkraftverk. Återställd från: energia-nuclear.net
- Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7: e. Ed. Cengage Learning. 618-622.
- Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. MacGraw Hill. 414-416.
- Walker, J. 2008. Fysik. 4: e utgåvan Addison Wesley. 610-630



Ingen har kommenterat den här artikeln än.