
Otto cykelfaser, prestanda, applikationer, lösta övningar
De Otto cyklar Det är en termodynamisk cykel som består av två isokoriska processer och två adiabatiska processer. Denna cykel inträffar på en komprimerbar termodynamisk vätska. Den skapades av den tyska ingenjören Nikolaus Otto i slutet av 1800-talet, som perfekterade förbränningsmotorn, föregångaren till den som finns i moderna bilar. Senare grundade hans son Gustav Otto det berömda BMW-företaget.
Otto-cykeln appliceras på förbränningsmotorer som arbetar med en blandning av luft och ett flyktigt bränsle som bensin, gas eller alkohol och vars förbränning startas med en elektrisk gnista.

Artikelindex
- 1 faser av Otto-cykeln
- 2 Ansökan
- 2.1 -Fyrataktsmotorn
- 3 Nettoarbete gjort i Otto-cykeln
- 3.1 Arbete utfört från A till B
- 3.2 Arbete utfört från C till D
- 4 Nettovärme i Otto-cykeln
- 5 Prestanda
- 6 Lösta övningar av Otto-cykeln
- 6.1-Övning 1
- 6.2-Övning 2
- 7 Referenser
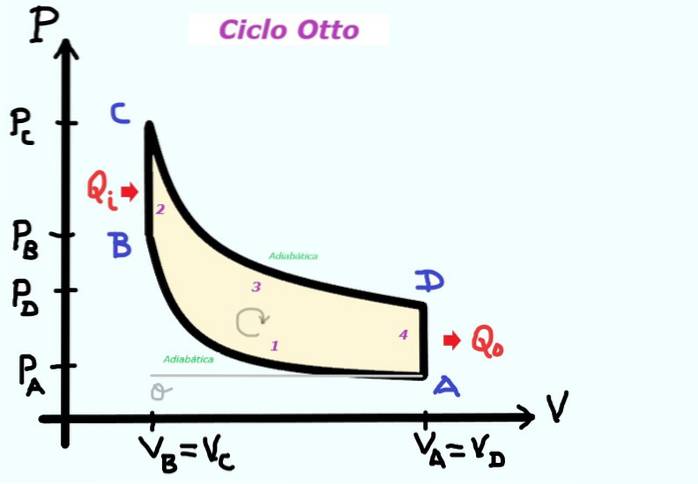
Faser av Otto-cykeln
Stegen i Otto-cykeln är:
- Adiabatisk kompression (inget värmeväxling med miljön).
- Absorption av värmeenergi i isokorisk form (utan att ändra volymen).
- Adiabatisk expansion (inget värmeväxling med miljön).
- Utsläpp av värmeenergi i isokorisk form (utan att ändra volymen).
Figur 2, som visas nedan, visar i ett PV-diagram (tryckvolym) de olika faserna i Otto-cykeln.
App
Otto-cykeln gäller lika för fyrtakts- och tvåtakts förbränningsmotorer.
-Fyrtaktsmotorn
Denna motor består av en eller flera kolvar i en cylinder, var och en med en (eller två) insugningsventiler och en (eller två) avgasventiler..
Det kallas så här eftersom dess operation har exakt fyra gånger eller väl markerade steg som är:
- Tillträde.
- Kompression.
- Explosionen.
- Flykten.
Dessa steg eller tider inträffar under vevaxelns två varv, eftersom kolven går ner och upp i tiderna 1 och 2 och återigen går ner och upp i tiderna 3 och 4.
Nedan beskriver vi i detalj vad som händer under dessa steg.
Steg 1
Sänka kolven från den högsta punkten med inloppsventilerna öppna och avgasventilerna stängda, så att luftbränsleblandningen dras in i kolven under sin nedstigning.
Intaget sker under steg OA i Otto-cykeldiagrammet vid atmosfärstryck PA. I detta steg har luft-bränsleblandningen införlivats, vilket är den komprimerbara vätskan på vilken stegen AB, BC, CD och DA i Otto-cykeln kommer att appliceras..
Steg 2
Strax innan kolven når den lägsta punkten stänger båda ventilerna. Sedan börjar den stiga på ett sådant sätt att den komprimerar luft-bränsleblandningen. Denna komprimeringsprocess sker så snabbt att den ger nästan ingen värme åt omgivningen. I Otto-cykeln motsvarar det den adiabatiska processen AB.
Steg 3
Vid kolvens högsta punkt, med blandningen komprimerad och ventilerna stängda, uppstår explosiv förbränning av blandningen som initierats av gnistan. Denna explosion är så snabb att kolven knappt har sjunkit ner.
I Otto-cykeln motsvarar det BC-isokoriprocessen där värme injiceras utan märkbar volymförändring, vilket därmed ökar trycket i blandningen. Värmen tillhandahålls genom den kemiska reaktionen av förbränning av syre i luften med bränslet.
Steg 4
Högtrycksblandningen expanderar och får kolven att sjunka ner medan ventilerna förblir stängda. Denna process sker så snabbt att värmeväxlingen med utsidan är försumbar.
Vid denna tidpunkt utförs positivt arbete på kolven, som överförs av vevstången till vevaxeln och producerar drivkraften. I Otto-cykeln motsvarar det den adiabatiska process-CD: n.
Steg 5
Under slagets nedre del matas värme ut genom cylindern in i köldmediet utan att volymen förändras märkbart. I Otto-cykeln motsvarar det den isokoriska processen DA.
Steg 6
I den sista delen av kolvslaget utvisas den brända blandningen av avgasventilen som förblir öppen medan insugningsventilen är stängd. Flykten av förbrända gaser sker under steg AO i Otto-cykeldiagrammet..
Hela processen upprepas med inloppsventilen till en ny luft-bränsleblandning.

Nettoarbete gjort i Otto-cykeln
Otto-cykeln fungerar som en värmemotor och körs medurs.
Arbetet W utfört av en gas som expanderar väggarna som innehåller den beräknas med följande formel:

Där Vi är den initiala volymen och Vf den slutliga volymen.
I en termodynamisk cykel motsvarar nätarbetet det område som ingår i P - V-diagrammets cykel.
När det gäller Otto-cykeln motsvarar det det mekaniska arbetet som utförts från A till B plus det mekaniska arbetet som utförts från C till D. Mellan B och C är det utförda arbetet noll eftersom det inte sker någon volymförändring. På samma sätt mellan D och A är verket noll.
Arbete utfört från A till B.
Antag att vi börjar från punkt A, där dess volym Va, dess tryck Pa och dess temperatur Ta är kända..
Från punkt A till punkt B utförs en adiabatisk kompression. Under kvasistatiska förhållanden följer adiabatiska processer Poissons lag, som säger att:

Där γ är adiabatisk kvot definieras som kvoten mellan den specifika värmen vid konstant tryck och den specifika värmen vid konstant volym.

Så arbetet som utförts från A till B skulle beräknas av förhållandet:

Efter att ha tagit integralen och använt Poissons förhållande för den adiabatiska processen har vi:

Var r är kompressionsförhållandet r = Va / Vb.
Arbetet utfört från C till D.
På samma sätt beräknas arbetet från C till D av integralen:

Vems resultat är

Varelse r = Vd / Vc = Va / Vb kompressionsförhållande.
Nettoarbetet kommer att vara summan av de två jobben:

Nettovärme i Otto-cykeln
I processerna från A till B och från C till D utbyts inget värme eftersom de är adiabatiska processer.
För processen från B till C utförs inget arbete och värmen som överförs genom förbränning ökar gasens inre energi och därför dess temperatur från Tb till Tc.

På samma sätt sker i processen från D till A värmeöverföring som också beräknas som:

Nettovärmen blir:

Prestanda
Prestanda eller effektivitet hos en cyklisk motor beräknas genom att hitta kvoten mellan nettoarbetet och värmen som tillförs systemet för varje driftscykel..

Om i föregående uttryck de tidigare resultaten ersätts och antagandet görs att bränsleluftblandningen beter sig som en idealgas, uppnås cykelns teoretiska effektivitet, vilket bara beror på kompressionsförhållandet:

Otto cykel lösta övningar
-Övning 1
En bensin-fyrtaktsmotor med en förskjutning på 1500 cc och ett kompressionsförhållande på 7,5 fungerar i en miljö med atmosfärstryck på 100 kPa och 20 grader Celsius. Bestäm nettoarbetet per cykel. Antag att förbränningen bidrar med 850 Joule för varje gram luft-bränsleblandning.
Lösning
Netto-arbetsuttrycket hade tidigare beräknats:

Vi måste bestämma volymen och trycket vid punkterna B och C i cykeln för att bestämma nettoarbetet.
Volymen vid punkt A där cylindern har fyllts med luft-bensinblandningen är 1500 cc förskjutning. Vid punkt B är volymen Vb = Va / r = 200 cc.
Volymen vid punkt C är också 200 cc.
Beräkning av tryck vid A, B och C
Trycket vid punkt A är atmosfärstryck. Trycket vid punkt B kan beräknas med hjälp av Poissons förhållande för en adiabatisk process:

Med hänsyn till att blandningen huvudsakligen är luft som kan behandlas som en diatomisk idealgas, tar gamma-adiabatisk koefficient värdet 1,4. Då blir trycket vid punkt B 1837,9 kPa.
Volymen för punkt C är densamma som för punkt B, det vill säga 200 cc.
Trycket vid punkt C är högre än vid punkt B på grund av temperaturökningen orsakad av förbränning. För att beräkna det måste vi veta hur mycket värme förbränningen har bidragit med.
Värmen som orsakas av förbränningen är proportionell mot mängden blandning som förbränns.
Med den ideala gasekvationen av tillstånd:

Så värmen som bidragit från förbränningen är 1,78 gram x 850 Joule / gram = 1513 Joule. Detta orsakar en temperaturökning som kan beräknas från

Tb kan beräknas från tillståndsekvationen som resulterar i 718 K, så för våra data är det resulterande värdet av Tc 1902 K.
Trycket vid punkt C ges av tillståndsekvationen applicerad på den punkten vilket resulterar i 4868,6 kPa.
Nettoarbetet per cykel visar sig då vara 838,5 Joule.
-Övning 2
Bestäm motorns effektivitet eller prestanda från övning 1. Förutsatt att motorn fungerar vid 3000 rpm, bestäm effekt.
Lösning
Att dela upp nätverket med den tillförda värmen ger en effektivitet på 55,4%. Detta resultat sammanfaller med det som erhålls genom direkt tillämpning av formeln för effektivitet som en funktion av kompressionsförhållandet.
Kraft är det arbete som utförs per tidsenhet. 3000 varv / min motsvarar 50 varv per sekund. Men Otto-cykeln slutförs för vartannat varv, eftersom det är en fyrtaktsmotor, som vi förklarade tidigare..
Detta innebär att på en sekund upprepas Otto-cykeln 25 gånger så det utförda arbetet är 25 x 838,5 Joule på en sekund..
Detta motsvarar 20,9 kilowatt effekt motsvarande 28 hästkrafter.
Referenser
- Termodynamiska cykler. Återställd från: fis.puc.cl
- Martín, T. och Serrano, A. Otto cyklar. Återställd från: 2.montes.upm.es.
- Sevilla universitet. Wiki från Institutionen för tillämpad fysik Otto cykel fallstudie. Återställd från: laplace.us.es.
- Wikipedia. Otto cyklar. Återställd från: es.wikipedia.com
- Wikipedia. Otto-motor. Återställd från: es.wikipedia.com



Ingen har kommenterat den här artikeln än.