Heter Betydande siffror till antalet siffror som finns i mantissa av ett nummer. Ju fler siffror du har, desto mer exakt är kvantiteten känd. Som en påminnelse är mantissan den siffra som följer kraften på 10 när siffran är skriven i vetenskaplig notation..
Låt oss till exempel ta siffran 0,00376, som skrivs som 3,76 x 10 -3. Mantissen är 3,76 och antalet har totalt 3 signifikanta siffror. Siffran 0,129 har också 3 signifikanta siffror, medan 4,5 bara har 2.
Och vad händer när talet är ett heltal? Det betyder att det är känt med så mycket precision som möjligt, med andra ord, det har oändlig precision. När man till exempel räknar människor, djur eller föremål som böcker och telefoner är resultatet ett exakt heltal.
Om vi säger att det i en biograf finns 110 personer som tittar på en film är detta det exakta antalet, varken mer eller mindre, och det har 3 betydande siffror.
Betydande siffror hanteras av några enkla regler som lagras med lite övning, vilket vi kommer att se nedan..
Artikelindex
De ledande nollorna räknas inte som en signifikant siffra, så 0,045 och 4,5 har båda två signifikanta siffror, eftersom dessa börjar räknas från vänster och börjar från den första siffran som inte är noll.
Nollorna efter (till höger) den första signifikanta siffran räknas som en betydande siffra (så länge det är motiverat av mätinstrumentets precision).
Slutligen räknas nollarna i mitten också som en betydande siffra..
För siffror skrivna i vetenskaplig notation är alla siffror i mantissan betydande, och exponenten påverkar inte precisionen..
När du utför operationer med decimaler, till exempel vid beräkning av arealer eller andra liknande operationer, måste resultatet ha samma antal signifikanta siffror som kvantiteten med det minsta antalet signifikanta siffror som deltog i operationen. Denna regel gäller för alla aritmetiska operationer.
Nummerets tecken påverkar inte dess betydande siffror.
Vi kommer omedelbart att se några exempel på detta och alla andra regler.
Hitta hur många viktiga siffror som finns i vart och ett av dessa siffror.
a) 876
b) 1000,68
c) 0,00005026
d) 4.8
e) -6,99
a) 876 har tre signifikanta siffror.
b) 1000.68 har 6 signifikanta siffror, eftersom nollarna däremellan räknas som sådana.
c) I stället har 0.00005026 fyra signifikanta siffror. Observera att de 5 nollorna till vänster om 5 inte räknas som en signifikant siffra, utan 0 som ligger mellan 5 och 2 är..
d) 4.8 har två signifikanta siffror.
e) -6.99 har 3 signifikanta siffror.
Det är vanligt att mäta med mätinstrument, såsom måttband, klockor, termometrar, vågar och så vidare. Med hur många viktiga siffror ska vi rapportera de kvantiteter som vi mäter på detta sätt??
Det beror på uppskattningen av instrumentet som det mäts med. Låt oss ta ett exempel: mäta den yttre diametern på ett rör, med en graderad linjal och med en vernier eller tjocklek.
Vernier är ett instrument som mäter längder mycket exakt eftersom det har en extra liten skala, kallad nonieskala, vilket möjliggör större finhet, så att säga, vid mätning.
Det är mer exakt än en graderad linjal, för med den kan vi veta mer betydelsefulla figurer av en viss längd.
Det är därför det inte är meningsfullt att rapportera en omkrets på, till exempel, 35,88 cm om vi mäter det med ett måttband, eftersom detta instrument inte är tillräckligt noggrant för att rapportera så många signifikanta siffror..
Uppskattningen A av måttbandet ges av:
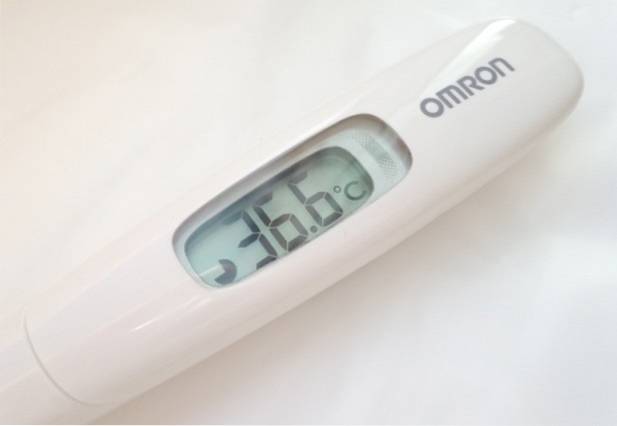
Hur många signifikanta siffror har avläsningen med den digitala termometern?
Termometern i figuren ger tresiffriga temperaturavläsningar. I mätningen som visas, 36,6 ºC, är dock bara de första två siffrorna från vänster till höger korrekta, eftersom decimaltal påverkas av instrumentets uppskattningsfel, vilket vanligtvis anges på instrumentets baksida eller i din bruksanvisning.
Det vanliga för den typ av digitalt instrument som visas är ett uppskattningsfel på 0,1 ºC. Detta räcker för att vara säker på att du inte har feber..
När du använder en miniräknare för att utföra beräkningar med erhållna mätningar är det inte korrekt att ge resultatet med alla siffror som visas på skärmen.
Endast de som är exakt kända behålls, eftersom bara de har verklig mening. Det är då nödvändigt att avrunda resultaten för att passa antalet exakt kända siffror. Dessa regler är:
-Om siffran efter siffran som ska hållas kvar är lika med eller större än 5, 1 läggs till denna siffra.
När vi till exempel avrundar 3.786 till två decimaler vill vi behålla siffrorna upp till 8. Eftersom antalet som följer (6) är större än 5 blir 8 till 8 + 1 = 9 och siffran förblir som 3,79.
-När siffran efter siffran som ska hållas är mindre än 5, siffran förblir densamma.
Om vi vill runda 1.27924 så att den bara har 3 decimaler uppnås detta genom att nå 9, vilket följs av 2. Eftersom 2 är mindre än 5 försvinner dessa decimaler och det rundade antalet förblir 1,279.
Ett matbord har form och mått som anges i den bifogade figuren. Du uppmanas att beräkna dess area med hjälp av reglerna för verksamheten med betydande siffror.
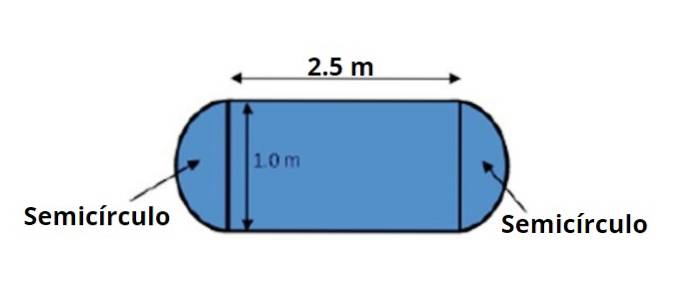
Tabellområdet kan delas in i ett centralt rektangulärt område och två halvcirklar, en på varje sida, som tillsammans gör en hel cirkel.
Vi kommer att ringa A1 till rektangelns område, ges av:
TILL1 = bas × höjd = 2,5 m x 1,0 m = 2,5 mtvå
För sin del är cirkelns yta, som är lika med den för en halvcirkel multiplicerad med 2:
TILLtvå = π × radietvå
Diametern på någon av halvcirklarna är 1,0 m, därför är radien 0,50 m. Diametern kan också användas direkt för att beräkna ytan, i detta fall:
TILLtvå = (π × diametertvå) / 4
Hur som helst:
TILLtvå = [π x (1,0 m)två] / 4 = 0,785398163 mtvå
Alla siffror från räknaren användes. Nu lägger vi till A1 redantvå för den totala ytan A i tabellen:
A = (2,5 + 0,785398163) mtvå = 3.285398163 mtvå
Eftersom måtten på tabellen är kända för två signifikanta siffror, är det inte meningsfullt att uttrycka resultatet med alla decimaler som räknaren ger, vilket aldrig ger antalet signifikanta siffror för ett resultat.
Vad du måste göra är att avrunda området så att det har samma antal signifikanta siffror som dimensionerna på tabellen, det vill säga 2. Det slutliga resultatet rapporteras därför enligt följande:
A = 3,3 mtvå
Ingen har kommenterat den här artikeln än.