De Poissons förhållande det är en måttlös kvantitet som är karakteristisk för varje material. Det är en indikation på deformationen av ett materialstycke innan vissa krafter appliceras.
När en bit material som utsätts för en spänning eller komprimering genomgår en deformation är kvoten mellan den tvärgående deformationen och den längsgående deformationen exakt Poissons förhållande.
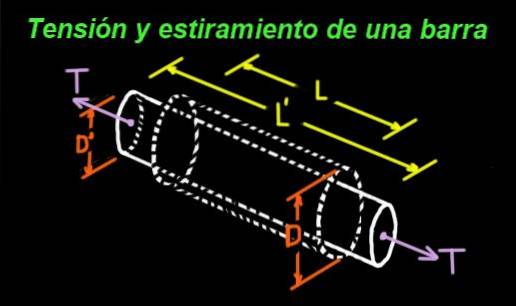
Till exempel sträcker sig en gummicylinder som är stressad i sina ändar i längdriktningen, men smalnar tvärs. Figur 1 visar en stapel vars ursprungliga mått är: längd L och diameter D.
Stången utsätts för en spänning T vid dess ändar, och som en följd av denna spänning genomgår den en sträckning, så att den nya längden är L '> L. Men när den sträcks, smalnar dess diameter också till det nya värdet: D' < D.
Kvoten mellan sträckan (positiv) och förminskningen (negativ) multiplicerad med (-1) är ett positivt tal mellan 0 och 0,5. Detta tal är det så kallade Poissons förhållande ν (grekiska bokstaven nu).
Artikelindex
För att beräkna Poissons förhållande är det nödvändigt att bestämma den längsgående och tvärgående töjningen.
Den längsgående töjningen εL är sträckan dividerad med den ursprungliga längden:
εL = (L '- L) / L.
På samma sätt kan den tvärgående stammen εT är den radiella konen dividerad med den ursprungliga diametern:
εT = (D '- D) / D.
Därför beräknas Poissons förhållande med följande formel:
ν = - εT / εL
Poissons förhållande ν, är relaterat till modulen OCH elasticitet (eller Youngs modul) och med styvhetsmodulen G, med följande formel:
v = E / (2G) - 1
En stång av ett visst plastmaterial har en längd av 150 mm och en cirkulär sektion av 20 mm i diameter. När den utsätts för en kompressionskraft F på 612,25 kg-f observeras en förkortning på 14 mm och samtidigt en ökning med 0,85 mm i stångens diameter.
Beräkna:
a) Längsgående töjning.
b) Den tvärgående stammen.
c) Poissons förhållande mellan det materialet.
d) Youngs elasticitetsmodul motsvarande materialet.
e) Styvhetsmodulen för den plasten.
Kom ihåg att den längsgående töjningen εL är sträckan dividerad med den ursprungliga längden:
εL = (L '- L) / L.
εL = (-14 mm) / 150 mm = -0,0933
Observera att den längsgående töjningen är dimensionell, och i det här fallet har den varit negativ eftersom den minskade sin längddimension.
På samma sätt är den tvärgående töjningen εT den radiella avsmalningen, dividerad med den ursprungliga diametern:
εT = (D '- D) / D
εT = (+0,85 mm) / 20 mm = 0,0425
Den tvärgående töjningen har varit positiv eftersom det har skett en ökning av stångens diameter.
För beräkningen av Poissons förhållande måste vi komma ihåg att det definieras som det negativa av kvoten mellan den tvärgående deformationen och den längsgående deformationen:
ν = - εT / εL
v = - 0,0425 / (-0,0933) = 0,4554
Man bör komma ihåg att Poissons förhållande är ett positivt måttlöst tal och för de flesta material är det mellan 0 och 0,5.
Youngs elasticitetsmodul, betecknad med bokstaven E, är proportionalitetskonstanten i Hookes lag. Med E är den normala spänningen σL relaterad till stammen εL enligt följande:
σL = E εL
Den normala spänningen definieras som kvoten mellan den normala kraften (i detta fall parallellt med stångens axel) och tvärsnittsarean:
σL = F / A = F / (π / 4 * D ^ 2)
I denna övning är kraften F 612,25 kg-f, som måste omvandlas till newton, vilket är SI-enheten:
F = 612,25 kg-f = 612,25 * 9,8 N = 6000 N = 6 kN
För sin del är tvärsnittet av område A:
A = (π / 4 * D ^ 2) = (3.1416 / 4) * (20 * 10 ^ -3 m) ^ 2 = 3.1416 * 10 ^ -4 m ^ 2
Slutligen är den normala spänningen som appliceras på stången:
σL = F / A = 6000 N / 3,1416 * 10 ^ -4 m ^ 2 = 19,098,593 Pa = 19,098 MPa
För att beräkna Youngs elasticitetsmodul löser vi E från Hookes lag σL = E εL:
E = σL / εL = 19,098,593 Pa / 0,0933 = 204,7 MPa
Styvhetsmodulen G är relaterad till Youngs modul E och Poissons förhållande ν med denna formel:
E / (2 G) = 1 + v
Därifrån kan du lösa för G:
G = E / (2 (1 + v)) = 204,7 MPa / (2 (1 + 0,4554)) = 70,33 MPa
Det finns en kopparkabel med en diameter på 4 mm och 1 m lång. Att veta att Youngs kopparmodul är 110 000 MPa och att Poissons förhållande är 0,34, uppskatta sträckningen och förminskningen i diameter som tråden genomgår när en vikt på 100 kg-f hängs på den..
Först är det nödvändigt att beräkna den normala dragspänningen som vikten utövar på tråden enligt denna formel:
σL = F / A = F / (π / 4 * D ^ 2)
Kraften F är 980 N och tvärsnittsarean är:
A = (π / 4 * D ^ 2) = (3.1416 / 4) * (4 * 10 ^ -3 m) ^ 2 = 1.2566 * 10 ^ -5 m ^ 2
Då är dragspänningen:
σL = 980 N / 1,2566 * 10 ^ -5 m ^ 2 = 77 986 000 Pa
Youngs elasticitetsmodul, betecknad med bokstaven E, är proportionalitetskonstanten i Hookes lag som relaterar den normala spänningen σL till stammen εL:
σL = E εL
Därifrån kan koppartrådens längsgående töjning lösas:
εL = σL / E = 77,986 MPa / 110000 MPa = 7,09 * 10 ^ -4
Å andra sidan, för att känna till den tvärgående stammen, tillämpas Poissons förhållande:
ν = - εT / εL
Slutligen har vi att den tvärgående stammen är:
εT = -ν εL = - 0,34 * 7,09 * 10 ^ -4 = -2,41 * 10 ^ -4
Slutligen, för att känna till kabelns absoluta sträcka, måste följande förhållande tillämpas:
ΔL = εL * L = 7,09 * 10 ^ -4 * 1 m = 7,09 * 10 ^ -4 m = 0,709 mm
Med den vikten sträckte sig kabeln knappt 0,709 millimeter.
För att uppnå den absoluta krympningen i diameter använder vi följande formel:
ΔD = εT * D = -2,41 * 10 ^ -4 * 4 mm = -9,64 * 10 ^ -4 mm = -0.000964 millimeter.
Denna förminskning i diameter är så liten att det är svårt att se med blotta ögat, även dess mätning kräver ett instrument med hög precision..
Ingen har kommenterat den här artikeln än.