De återbetalningskoefficient är kvoten mellan den relativa retirationshastigheten och den relativa inflygningshastigheten för två kolliderande kroppar. När kropparna förenas efter kollisionen är denna kvot noll. Och enheten är värt om kollisionen är helt elastisk.
Anta att två fasta masskulor M1 och massa M2 respektive som drabbas av en kollision. Strax före kollisionen hade kulorna hastigheter V1 Y V2 med avseende på ett visst tröghetsreferenssystem. Strax efter kollisionen ändras deras hastigheter till V1 ' Y V2 '.
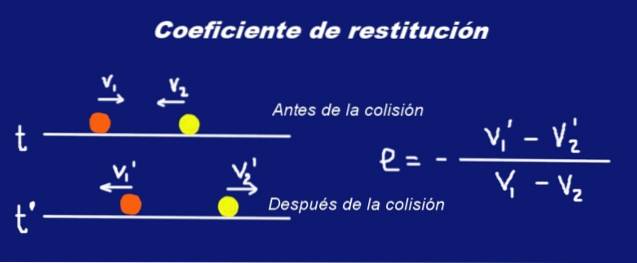
Brev har placerats fetstil i hastigheterna för att indikera att de är vektormängder.
Experiment indikerar att varje kollision uppfyller följande förhållande:
V1 ' - V2 '= -och (V1 - V2)
Var och är ett reellt tal mellan 0 och 1, kallat återbetalningskoefficient av kollisionen. Ovanstående uttryck tolkas så här:
Den relativa hastigheten för två partiklar före kollisionen är proportionell mot den relativa hastigheten för de två partiklarna efter kollisionen, proportionalitetskonstanten är (-e), där e är kollisionens återställningskoefficient.
Artikelindex
Nyttan med denna koefficient ligger i att känna till grad av oelasticitet av en kollision. Om kollisionen är helt elastisk, kommer koefficienten att vara 1, medan koefficienten vid en helt oelastisk kollision är 0, eftersom i detta fall är den relativa hastigheten efter kollisionen noll..
Omvänt, om återställningskoefficienten för en kollision och partiklarnas hastigheter innan den är kända, kan hastigheterna efter kollisionen förutsägas..
Vid kollisioner, förutom förhållandet som fastställer återställningskoefficienten, finns det en annan grundläggande relation, som är bevarande av fart.
Momentum sid av en partikel, eller momentum som det också kallas, är massprodukten M av partikeln genom dess hastighet V. Det vill säga: momentum sid är en vektorkvantitet.
Vid kollisioner den linjära momentum P av systemet är detsamma precis före och strax efter kollisionen, eftersom de yttre krafterna är försumbara jämfört med de korta men intensiva inre interaktionskrafterna under kollisionen. Men bevarande av fart är inte tillräckligt P av systemet för att lösa det allmänna problemet med kollision.
I det tidigare nämnda fallet, för de två kolliderande sfärerna för massorna M1 och M2, skrivs bevarande av linjär momentum enligt följande:
M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .
Det finns inget sätt att lösa kollisionsproblemet om återställningskoefficienten inte är känd. Bevarande av fart, även om det är nödvändigt, är inte tillräckligt för att förutsäga hastigheter efter kollision.
När ett problem säger att kropparna rör sig tillsammans efter kollisionen säger det implicit att återställningskoefficienten är 0.
Den andra viktiga fysiska storleken som är involverad i kollisioner är energi. Under kollisioner utbyts kinetisk energi, potentiell energi och andra typer av energi, såsom värmeenergi.
Före och efter kollisionen är interaktionens potentiella energi praktiskt taget noll, så energibalansen involverar den kinetiska energin hos partiklarna före och efter och en kvantitet F kallas försvunnen energi.
För de två kolliderande masskulorna M1 och M2 skrivs energibalansen före och efter kollisionen enligt följande:
½ M1 V1^ 2 + ½ M2 V2^ 2 = ½ M1 V1 '^ 2 + ½ M2 V2 '^ 2 + Q
När interaktionskrafterna under kollisionen är rent konservativa händer det att total kinetisk energi av de kolliderande partiklarna är konserverade, det vill säga det är detsamma före och efter kollisionen (Q = 0). När detta händer sägs kollisionen vara helt elastisk..
I fall av elastiska kollisioner försvinner ingen energi. Och dessutom överensstämmer återbetalningskoefficienten med: e = 1.
Tvärtom, i de oelastiska kollisionerna Q ≠ 0 och 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.
För att ett kollisionsproblem ska vara perfekt bestämt är det nödvändigt att känna till återställningskoefficienten, eller alternativt mängden energi som försvinner under kollisionen.
Restitutionskoefficienten beror på naturen och typen av interaktion mellan de två kropparna under kollisionen..
För sin del kommer kroppens relativa hastighet före kollisionen att definiera interaktionsintensiteten och därmed dess inflytande på återställningskoefficienten..
För att illustrera hur beräkningskoefficienten för en kollision beräknas tar vi ett enkelt fall:
Antag att kollisionen mellan två masskulor M1 = 1 kg Y M2 = 2 kg rör sig på en rak skena utan friktion (som i figur 1).
Den första sfären träffar med inledande hastighet V1 = 1 m / s på den andra som ursprungligen vilar, det vill säga V2 = 0 m / s.
Efter kollisionen fortsätter de att röra sig så här: den första stannar (V1 '= 0 m / s) och den andra rör sig åt höger med hastighet V2 '= 1/2 m / s.
För att beräkna återställningskoefficienten i denna kollision tillämpar vi förhållandet:
V1 ' - V2 ' = -och ( V1 - V2 )
0 m / s - 1/2 m / s = - e (1 m / s - 0 m / s) => - 1/2 = - e => e = 1/2 .
Vid den endimensionella kollisionen mellan de två sfärerna i föregående avsnitt beräknades deras återställningskoefficient, vilket resulterade i e = ½ .
Eftersom e ≠ 1 är kollisionen inte elastisk, det vill säga systemets kinetiska energi bevaras inte och det finns en viss mängd försvunnen energi Q (till exempel uppvärmning av sfärerna på grund av kollisionen).
Bestäm värdet på den energi som försvinner i Joule. Beräkna också den procentuella andelen energi som försvinner.
Den ursprungliga kinetiska energin för sfär 1 är:
K1i = ½ M1 V1 ^ 2 = ½ 1 kg (1 m / s) ^ 2 = ½ J
medan sfären 2 är noll eftersom den initialt är i vila.
Då är systemets initiala kinetiska energi Ki = ½ J.
Efter kollisionen rör sig bara den andra sfären med hastigheten V2 '= ½ m / s, så den slutliga kinetiska energin i systemet blir:
Kf = ½ M2 V2 '^ 2 = ½ 2 kg (½ m / s) ^ 2 = ¼ J
Det vill säga den energi som försvinner i kollisionen är:
Q = Ki - Kf = (½ J - ¼ J) = 1/4 J
Och den bråkdel av energi som försvinner vid denna kollision beräknas enligt följande:
f = Q / Ki = ¼ / ½ = 0,5, det vill säga att 50% av systemets energi har försvunnit på grund av den oelastiska kollisionen vars återställningskoefficient är 0,5.
Ingen har kommenterat den här artikeln än.