Styv kropp

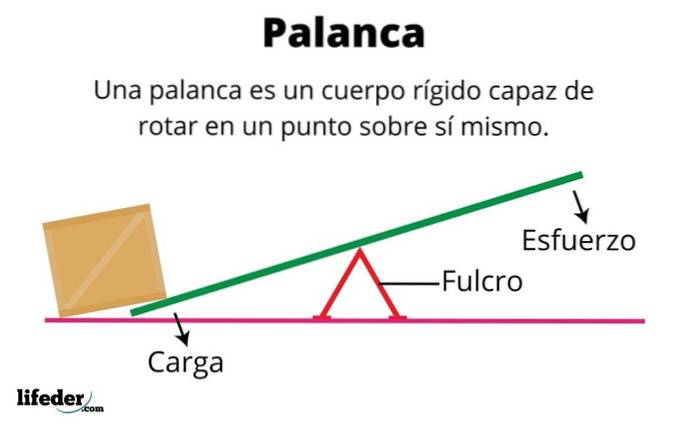
Vad är en stel kropp?

En styv kropp är ett materialföremål vars partiklar alltid förblir i samma relativa positioner. Därför är det ett objekt som inte deformeras, en kvalitet som tillskrivs de starka sammanhållningskrafterna som håller partiklarna på plats..

I verkligheten tenderar partiklarna i varje kropp som utsätts för yttre krafter att vibrera eller röra sig, så objektet deformeras alltid i viss utsträckning, men dessa effekter är vanligtvis små.

När detta är fallet kan det antas att kroppen är stel och har en mycket bra uppskattning av sitt beteende, även om det är en idealisering.

Styva kroppstyper

Två typer av styv kropp kan särskiljas:

• De vars partiklar kommer i diskreta mängder, det vill säga de kan räknas. Till exempel kan två metallkulor förenas av en tunn och lätt stav betraktas som en enda enhet. Om stången är tillräckligt styv för att inte böjas anses systemet vara en stel kropp.
• De som är kontinuerliga, vilket innebär att partiklarna som utgör dem är oskiljbara. Vardagliga föremål och natur är bra exempel: stenar, möbler och andra, liksom jorden och andra steniga himmellegemer.

Styv kroppsrörelse och dynamik

Liksom föremål som betraktas som partiklar kan styva kroppar översättas, rotera och ha en mer allmän rörelse, som kombinerar translation och rotation.

För att studera översättningen är det inte nödvändigt att analysera rörelsen för varje partikel separat, utan snarare rörelsen av masscentrum, en punkt där det anses att hela objektets massa är koncentrerad..

Dessa translationella och roterande rörelser kan vara:

• Oberoende, som i fallet med planeter, som har en rotationsrörelse runt sin axel (anses vara fixerad) och en översättningsrörelse runt solen, men hastigheterna för var och en är inte relaterade..
• Roto-översättning, om vinkelhastigheten och translationens hastighet för masscentrum är relaterade. I detta fall är rotationsaxeln rörlig, som i fallet med cylindern som rullar nerför en brant sluttning utan att glida..

Den styva kroppens dynamik

Följande mängder är relevanta i den styva kroppens dynamik:

Masscenter

Masscentrum är den punkt där hela kroppens massa anses vara koncentrerad. Om det är en homogen och symmetrisk kropp, såsom en sfär, sammanfaller masscentrum med det geometriska centrumet.

Tröghetsmoment

Denna skalära storlek är värdet av rotationsinerti eller motstånd som ett objekt motsätter sig för att rotera runt en viss axel. Det beror helt på objektets geometri och dess massa och därför är det i vissa fall lättare att rotera runt vissa axlar än andra..

För kroppar med väldefinierade geometriska former finns det tabeller med tröghetsmomenten med avseende på symmetriaxlarna, till exempel den som passerar genom massacentret. Med denna information och satser relaterade till tröghetsmomentet kan ögonblicken om andra axlar lätt beräknas..

Krafter och vridmoment eller vridmoment

Det krävs krafter för att flytta en kropp. Om masscentrum för det styva fasta ämnet översätts är rörelseekvationen enligt Newtons andra lag:

F_netto = M ∙till_centimeter

Var:

-Nettokraften är F_netto

-M är massan

-Accelerationen av masscentrum är till_centimeter

Men inte alla de applicerade krafterna lyckas få objektet att rotera. Detta kräver vridmoment eller vridmoment, vilket berättar hur effektiv en krafts rotationsverkan är. Det definieras som vektorprodukten mellan positionsvektorn r med avseende på en viss punkt O och kraften F i fråga. Det betecknas med det grekiska brevet τ (i fetstil, eftersom det också är en vektor):

τ = r × F

I SI International System är enheten för vridmoment N⋅m (newton per meter).

I många fall beskrivs rotationsrörelse kring en axel genom massacentret med en ekvation som är analog med Newtons andra lag:

Kinetisk energi av ett fast ämne

En styv kropps rörelse beskrivs av översättningar av masscentrum och rotationer runt den punkten, därför har dess kinetiska energi båda bidrag.

Låt K vara kroppens kinetiska energi, v_centimeter massacentrets hastighet, M kroppens massa, I_centimeter dess tröghetsmoment om masscentrum och ω vinkelhastigheten. Det kan visas att den kinetiska energin är:

K = ½ Mv_centimeter^två + ½ jag_centimeter ω^två

Det observeras att den andra termen till höger är rotationsanalogen till termen till vänster. Där spelar tröghetsmomentet samma roll som massan, medan vinkelhastigheten har samma roll som den linjära hastigheten..

Exempel i vardagen

Fysisk pendel

Den fysiska pendeln eller den verkliga pendeln är väldigt lätt att bygga: den består av ett styvt fast ämne, såsom en stång eller stång, fritt oscillerande runt en horisontell axel. Rotationsaxeln passerar inte genom objektets masscentrum och detta kan i princip ha någon form.

Denna pendel skiljer sig från den enkla pendeln, för i den senare anses massan som komponerar den vara punktlig.

Cykelhjul

Ett annat exempel på en välkänd styv kropp är cykelhjulet, vars axel passerar genom massacentret, som passerar genom hjulets centrum. Så länge det inte lutar åt sidan eller vänder, gäller ekvationerna för dynamik som beskrivs ovan för att beskriva dess rörelse..

En bowlingboll

Styv solid modell är väl lämpad för att beskriva bowlingkulrörelser på banan eller vid rullning utan att glida nerför returrampen.

Yoyo

Den här populära leksaken är gjord med en trä- eller plastcylinder och ett snöre lindat i ett spår som omger den..

Cylindern kan modelleras som en stel kropp i vilken spänningen i strängen ger vridmomentet, medan vikten (applicerad på masscentrum) och spänningen är ansvariga för den vertikala accelerationen av masscentrumet..

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 
2. Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
3.  Katz, D. 2013. Fysik för forskare och ingenjörer. Grunder och anslutningar. Cengage Learning.
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Red. Volym 1. Pearson.
5. Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7: e. Ed. Cengage Learning.