De skillnader mellan hastighet och hastighet de finns, även om de båda är relaterade fysiska mängder. På vanligt språk används den ena termen eller den andra omväxlande som om de vore synonymer, men inom fysik är det nödvändigt att skilja mellan dem..
Denna artikel definierar båda begreppen, pekar på skillnaderna och förklarar, med hjälp av exempel, hur och när den ena eller den andra tillämpas. För att förenkla överväger vi en partikel i rörelse och därifrån kommer vi att granska begreppen hastighet och hastighet.
| Hastighet | Hastighet | |
| Definition | Det är det avstånd som har rest per tidsenhet. | Det är förskjutningen (eller förändring av position) i varje tidsenhet. |
| Notation | v | v |
| Matematisk objekttyp | Klättra. | Vektor. |
| Formel (under en begränsad tidsperiod) * | v = As / At | v = Ar / At |
| Formel (för en viss tid) ** | v = ds / dt = s '(t) | v = dr / dt = r '(t) |
| Förklaring av formeln | * Ruttens längd dividerat med den tidsperiod som används för att köra den. ** I ögonblicklig hastighet tenderar tidsperioden att vara noll. | * Vektorförskjutning dividerat med den tid som förskjutningen inträffade. |
| Egenskaper | För att uttrycka det krävs endast ett positivt reellt tal, oavsett de rumsliga dimensioner där rörelsen sker.. | Det kan ta mer än ett reellt tal (positivt eller negativt) för att uttrycka det, beroende på de rumsliga dimensioner där rörelsen sker.. |
Olika aspekter av hastighet och hastighet sammanfattades i tabellen ovan. Och som komplement betraktas flera exempel som illustrerar de inblandade begreppen och deras relationer:
Antag att en röd myra rör sig längs en rak linje och i den riktning som anges i figuren nedan.
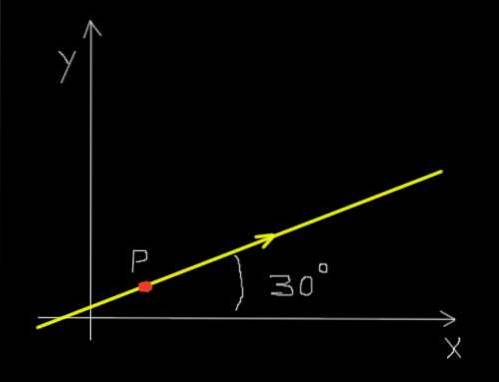
Dessutom rör sig myran jämnt på ett sådant sätt att den färdas ett avstånd av 30 millimeter under en tidsperiod av 0,25 sekunder..
Bestäm hastigheten och hastigheten på myran.
Myrans hastighet beräknas genom att dela avståndet As reste mellan tiden At.
v = Δs / Δt = (30 mm) / (0,25 s) = 120 mm / s = 12 cm / s
Myrans hastighet beräknas genom att dela förskjutningen Δr mellan den tidsperiod då förskjutningen gjordes.
Förskjutningen var 30 mm i 30º-riktningen i förhållande till X-axeln, eller i kompakt form:
Δr = (30 mm ¦ 30º)
Det kan noteras att förskjutningen består av en storlek och en riktning, eftersom det är en vektormängd. Alternativt kan förskjutningen uttryckas enligt dess kartesiska komponenter X och Y på detta sätt:
Δr = (30 mm * cos (30º); 30 mm * sin (30º)) = (25,98 mm; 15,00 mm)
Myrans hastighet beräknas genom att dela förskjutningen med den tidsperiod den gjordes:
v = Δr/ At = (25,98 mm / 0,25 sek; 15,00 mm / 0,25 sek) = (103,92; 60,00) mm / sek
Denna hastighet i kartesiska komponenterna X och Y och i enheter av cm / s är:
v = (10,392; 6,000) cm / s.
Alternativt kan hastighetsvektorn uttryckas i sin polära form (modul ¦ riktning) såsom visas:
v = (12 cm / s ¦ 30º).
Notera: i detta exempel, eftersom hastigheten är konstant, sammanfaller medelhastigheten och den momentana hastigheten. Modulen för den momentana hastigheten befinner sig vara den momentana hastigheten.
Samma myra i föregående exempel går från A till B, sedan från B till C och slutligen från C till A, enligt den triangulära vägen som visas i följande figur.
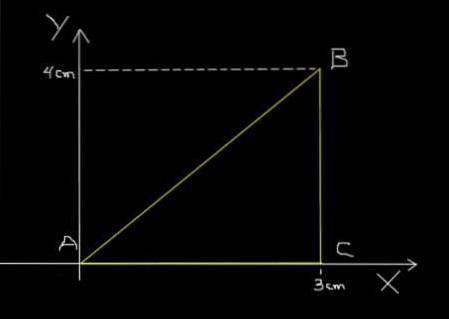
Avsnitt AB täcker det på 0,2 sek. BC går igenom den på 0,1 sekunder och slutligen går CA igenom den på 0,3 sekunder. Beräkna medelhastigheten för resan ABCA och medelhastigheten för resan ABCA.
För att beräkna myrans medelhastighet börjar vi med att bestämma den totala sträckan:
As = 5 cm + 4 cm + 3 cm = 12 cm.
Tiden som används för hela resan är:
At = 0,2 s + 0,1 s + 0,3 s = 0,6 s.
Så myrans medelhastighet är:
v = As / At = (12 cm) / (0,6 s) = 20 cm / s.
Därefter beräknas myrans medelhastighet i ABCA-rutten. I detta fall är myrans förskjutning:
Δr = (0 cm; 0 cm)
Detta beror på att förskjutningen är skillnaden mellan slutpositionen minus startpositionen. Eftersom båda positionerna är desamma är deras skillnad noll, vilket resulterar i en nollförskjutning.
Denna nollförskjutning utfördes under en tidsperiod på 0,6 sekunder, så myrans medelhastighet var:
v =(0 cm; 0 cm) / 0,6 s = (0; 0) cm / s.
Avslutning: medelhastighet 20 cm / s, men medelhastigheten är noll i ABCA-rutten.
En insekt rör sig på en cirkel med en radie på 0,2 m med jämn hastighet, så att den, från A och anländer till B, färdas ¼ med en omkrets på 0,25 s.
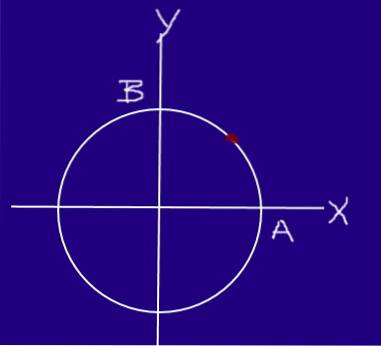
Bestäm insektens hastighet och hastighet i avsnitt AB.
Längden på omkretsbågen mellan A och B är:
As = 2πR / 4 = 2π (0,2 m) / 4 = 0,32 m.
Tillämpa definitionen av medelhastighet har vi:
v = As / At = 0,32 m / 0,25 s = 1,28 m / s.
För att beräkna medelhastigheten är det nödvändigt att beräkna förskjutningsvektorn mellan startpositionen A och slutpositionen B:
Δr = (0, R) - (R, 0) = (-R, R) = (-0,2, 0,2) m
Genom att använda definitionen av medelhastighet får vi:
v = Δr/ At = (-0,2, 0,2) m / 0,25 s = (-0,8, 0,8) m / s.
Det tidigare uttrycket är medelhastigheten mellan A och B uttryckt i kartesisk form. Alternativt kan medelhastigheten uttryckas i polär form, det vill säga modul och riktning:
| v | = ((-0,8) ^ 2 + 0,8 ^ 2) ^ (½) = 1,13 m / s
Riktning = arctan (0,8 / (-0,8)) = arctan (-1) = -45º + 180º = 135º med avseende på X-axeln.
Slutligen är medelhastighetsvektorn i polär form: v =(1,13 m / s ¦ 135º).
Om vi antar att insekttidens starttid i det föregående exemplet är 0s från punkt A, har vi att dess positionsvektor vid varje ögonblick ges av:
r(t) = [R cos ((π / 2) t); R sin ((π / 2) t)].
Bestäm hastighet och momentan hastighet för varje ögonblick t.
Den momentana hastigheten är derivatet med avseende på tid för positionsfunktionen:
v(t) = dr/ dt = [-R (π / 2) sin ((π / 2) t); R (π / 2) cos ((π / 2) t)]
Den momentana hastigheten är modulen för den momentana hastighetsvektorn:
v (t) = | v(t) | = π R / 2 ^ ½
Ingen har kommenterat den här artikeln än.