
Ytvidgningsformel, koefficienter och exempel
De ytlig utvidgning Det är expansionen som uppstår när ett objekt upplever variationer i ytan på grund av en variation i temperaturen. Det beror på egenskaperna hos materialet eller dess geometriska form. Utvidgningen dominerar i två dimensioner i samma proportion.
Till exempel, i ett ark, när det sker en temperaturförändring, är det ytan på arket som genomgår den största förändringen på grund av termisk expansion..

Metallplåten enligt föregående figur ökar dess bredd och längd avsevärt när den värms upp av solstrålning. Tvärtom minskar båda betydligt när det kyls på grund av en minskning av omgivningstemperaturen..
Det är av den anledningen att kanterna inte ska klibba ihop när plattor installeras på ett golv, men det bör finnas ett gap som kallas en expansionsfog..
Dessutom är detta utrymme fyllt med en speciell blandning som har en viss grad av flexibilitet, vilket förhindrar att brickorna spricker på grund av de starka tryck som termisk expansion kan ge..
Artikelindex
- 1 Vad är ytlig utvidgning?
- 2 Ytvidgning och dess koefficient
- 3 Ytutvidgningskoefficient för olika material
- 4 Arbetade exempel på ytutvidgning
- 4.1 Exempel 1
- 4.2 Exempel 2
- 5 Referenser
Vad är ytlig utvidgning?
I ett fast material behåller atomerna sina relativa positioner mer eller mindre fixerade runt en jämviktspunkt. Men på grund av termisk omrörning oscillerar de alltid runt samma.
När temperaturen ökar ökar också den termiska svängningen, vilket gör att mellersta svängningspositioner ändras. Detta beror på att bindningspotentialen inte är exakt parabolisk och har asymmetri runt det minsta.
Nedan är en figur som beskriver den kemiska bindningsenergin som en funktion av det interatomära avståndet. Den totala svängningsenergin vid två temperaturer och hur svängningens centrum rör sig visas också..
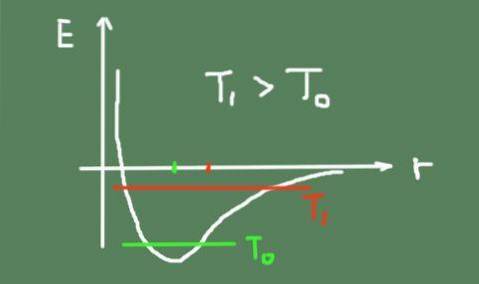
Ytlig utvidgning och dess koefficient
För att mäta ytans utvidgning börjar vi från ett initialområde A och en initial temperatur T för objektet vars utvidgning ska mätas..
Antag att objektet är ett ark av område A, och dess tjocklek är mycket mindre än kvadratroten av område A. Arket utsätts för en temperaturvariation AT, så att dess slutliga temperatur när den termiska jämvikten med värmekällan har är det T '= T + AT.
Under denna termiska process kommer också ytarean att ha ändrats till ett nytt värde A '= A + ΔA, där ΔA är längdförändringen. Således definieras ytexpansionskoefficienten σ som kvoten mellan den relativa variationen av arean per enhet av temperaturvariation.
Följande formel definierar ytutvidgningskoefficienten σ:
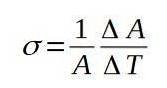
Koefficienten för ytutvidgning σ är praktiskt taget konstant över ett brett intervall av temperaturvärden.
Enligt definitionen av σ är dess dimensioner inversa av temperaturen. Enheten är vanligtvis ° C-1.
Ytutvidgningskoefficient för olika material
Därefter ger vi en lista över ytlig expansionskoefficient för vissa material och element. Koefficienten beräknas vid normalt atmosfärstryck baserat på en omgivningstemperatur på 25 ° C, och dess värde anses vara konstant inom ett område av AT från -10 ° C till 100 ° C.
Enheten för ytutvidgningskoefficienten kommer att vara (° C)-1
- Stål: σ = 24 ∙ 10-6 (° C)-1
- Aluminium: σ = 46 ∙ 10-6 (° C)-1
- Guld: σ = 28 ∙ 10-6 (° C)-1
- Koppar: σ = 34 ∙ 10-6 (° C)-1
- Mässing: σ = 36 ∙ 10-6 (° C)-1
- Järn: σ = 24 ∙ 10-6 (° C)-1
- Glas: σ = (14 till 18) ∙ 10-6 (° C)-1
- Kvarts: σ = 0,8 ∙ 10-6 (° C)-1
- Diamant: σ = 2 ,, 4 ∙ 10-6 (° C)-1
- Bly: σ = 60 ∙ 10-6 (° C)-1
- Ekved: σ = 108 ∙ 10-6 (° C)-1
- PVC: σ = 104 ∙ 10-6 (° C)-1
- Kolfiber: σ = -1,6 ∙ 10-6 (° C)-1
- Betong: σ = (16 till 24) ∙ 10-6 (° C)-1
De flesta material sträcker sig med en ökning av temperaturen. Vissa material som kolfiber krymper dock med ökande temperatur..
Arbetade exempel på ytutvidgning
Exempel 1
En stålplåt har måtten 3m x 5m. På morgonen och i skuggan är temperaturen 14 ° C, men vid middagstid värmer solen upp till 52 ° C. Hitta den sista delen av plattan.
Lösning
Vi utgår från definitionen av ytutvidgningskoefficienten:
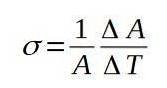
Härifrån löser vi variationen i området:
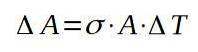
Vi fortsätter sedan med att ersätta respektive värden för att hitta ökningen i område med temperaturökningen.
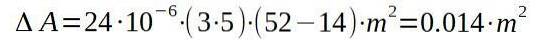
Det vill säga den slutliga ytan blir 15 014 kvadratmeter.
Exempel 2
Visa att ytutvidgningskoefficienten är ungefär dubbelt så stor som den linjära expansionskoefficienten.
Lösning
Anta att vi börjar från en rektangulär platta med måtten bredd Lx och längd Ly, då blir dess ursprungliga yta A = Lx ∙ Ly
När plattan genomgår en temperaturökning ΔT, ökar dess dimensioner till dess nya bredd Lx 'och dess nya längd Ly', så att dess nya område blir A '= Lx' ∙ Ly '

Variationen som påverkas av plattans område på grund av temperaturförändringen kommer då att vara
ΔA = Lx '∙ Ly' - Lx ∙ Ly
där Lx '= Lx (1 + α ΔT) och Ly' = Ly (1 + α ΔT)
Det vill säga förändringen i område som en funktion av koefficienten för linjär expansion och temperaturförändringen kommer att vara:
ΔA = Lx (1 + α ΔT) ∙ Ly (1 + α ΔT) - Lx ∙ Ly
Detta kan skrivas om som:
ΔA = Lx ∙ Ly ∙ (1 + α ΔT) ² - Lx ∙ Ly
Att utveckla torget och multiplicera har vi följande:
ΔA = Lx ∙ Ly + 2α ΔT Lx ∙ Ly + (α ΔT) ² Lx ∙ Ly - Lx ∙ Ly
Eftersom α är i storleksordningen 10-6, när den är kvadratisk är den i storleksordningen 10-12. Sålunda är den kvadratiska termen i ovanstående uttryck försumbar.
Då kan arealökningen approximeras med:
ΔA ≈ 2α ΔT Lx ∙ Ly
Men arealökningen som en funktion av ytutvidgningskoefficienten är:
ΔA = γ ΔT A
Från vilket ett uttryck härleds som relaterar koefficienten för linjär expansion med koefficienten för ytexpansion.
γ ≈ 2 ∙ α
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mac Graw Hill. 422-527
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Utgåva. Prentice Hall. 238-249.


Ingen har kommenterat den här artikeln än.