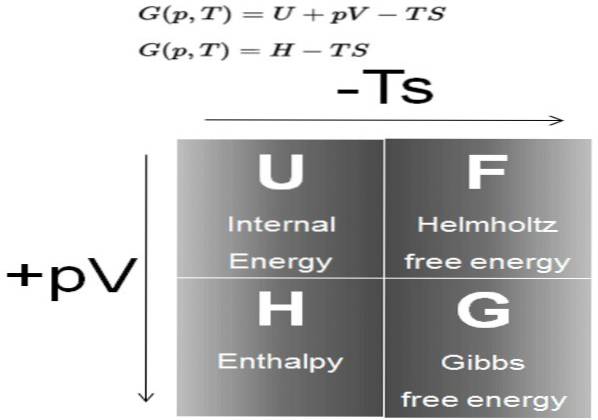
De Gibbs fri energi (vanligtvis kallad G) är en termodynamisk potential definierad som skillnaden mellan entalpi H minus produkten av temperaturen T av systemets entropi S:
G = H - T S
Gibbs fri energi mäts i Joule (enligt International System), i ergs (för Cegesimal System of Units), i kalorier eller i elektronvolt (för elektriska volt).
I processer som uppträder vid konstant tryck och temperatur är variationen av Gibbs fri energi ΔG = ΔH - T ΔS. I sådana processer representerar (G) den energi som finns tillgänglig i systemet som kan omvandlas till arbete.
Till exempel i exoterma kemiska reaktioner minskar entalpi medan entropi ökar. I Gibbs-funktionen motverkas dessa två faktorer, men först när Gibbs-energin minskar inträffar reaktionen spontant..
Så, om variationen av G är negativ, är processen spontan. När Gibbs-funktionen når sitt minimum når systemet ett stabilt jämviktsläge. Sammanfattningsvis kan vi bekräfta i en process där tryck och temperatur är konstanta:
- Om processen är spontan, då ΔG < 0
- När systemet är i jämvikt: ΔG = 0
- I en icke-spontan process ökar G: ΔG> 0.
Artikelindex
Gibbs fria energi (G) beräknas med hjälp av definitionen i början:
G = H - T⋅S
I sin tur är entalpi H en termodynamisk potential definierad som:
H = U + P V
Därefter kommer en steg-för-steg-analys att göras för att känna till de oberoende variablerna som Gibbs-energin är en funktion av:
1 - Från den första lagen om termodynamik har vi att den inre energin U är relaterad till systemets entropi S och dess volym V för reversibla processer genom differentieringsförhållandet:
dU = dQ - dW = TdS - PdV
Av denna ekvation följer att den interna energin U är en funktion av variablerna S och V:
U = U (S, V)
2- Med utgångspunkt från definitionen av H och tar differentialen får vi:
dH = dU + d (P V) = dU + VdP + PdV
3- Att ersätta uttrycket för dU erhållet i (1) har vi:
dH = TdS - PdV + VdP + PdV = TdS + VdP
Av detta dras slutsatsen att entalpi H beror på entropin S och trycket P, det vill säga:
H = H (S, P)
4- Nu beräknas den totala skillnaden mellan fri energi från Gibbs och erhåller:
dG = dH -TdS -SdT = TdS + VdP -TdS -SdT
Där dH har ersatts med uttrycket i (3).
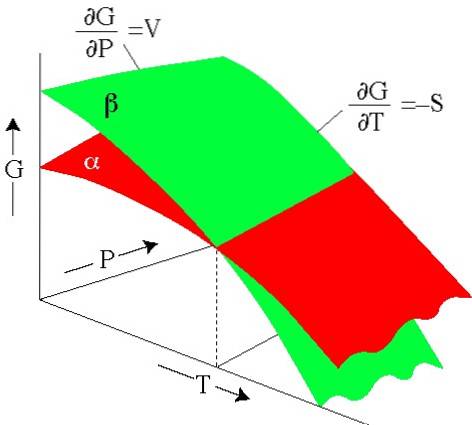
5- Slutligen, när vi förenklar, får vi: dG = VdP - SdT, vara tydlig att den fria energin G beror på trycket och temperaturen T som:
G = G (P, T)
Av analysen i föregående avsnitt följer att den inre energin i ett system är en funktion av entropi och volym:
U = U (S, V)
Sedan är skillnaden på ELLER kommer vara:
dU = ∂SU |V dS + ∂VU |S dV = TdS - PdV
Från detta partiella derivatuttryck kan de så kallade Maxwell-termodynamiska relationerna härledas. Delderivat gäller när en funktion beror på mer än en variabel och beräknas enkelt genom att tillämpa satsen i nästa avsnitt.
∂VT |S = -∂SP |V
För att komma fram till detta förhållande, Clairaut-Schwarz sats på partiella derivat, som anger följande:
"De blandade derivaten av andra ordningen med de utbytta variablerna är lika, så länge som funktionerna som ska härledas är kontinuerliga och differentierbara".
Baserat på vad som visas i punkt 3 i föregående avsnitt:
H = H (S, P) och dH = TdS + VdP
Det kan erhållas:
∂PT |S = ∂SV |P
Vi fortsätter på liknande sätt med Gibbs fri energi G = G (P, T) och med Helmholtz fri energi F = F (T, V) för att få de andra två Maxwell-termodynamiska förhållandena.
1- Associerad med den interna energin U: ∂VT |S = -∂SP |V
2- Den som erhållits från entalpi H: ∂PT |S = ∂SV |P
3- Relaterat till Helmholtz-energin F: ∂TP |V = ∂VS |T
4- Länkad till Gibbs fria energi G: ∂TV |P = -∂PS |T
Beräkna variationen av Gibbs fria energi för 2 mol idealgas vid en temperatur på 300K under en isotermisk expansion som tar systemet från en initial volym på 20 liter till en slutvolym på 40 liter.
Vi påminner om definitionen av Gibbs fri energi som vi har:
G = H - T S
Då kommer en ändlig variation av F att vara:
ΔG = ΔH - T ΔS, sedan AT = 0
I ideala gaser beror entalpi bara på dess absoluta temperatur, men eftersom det är en isotermisk process är ΔH = 0 och ΔG = - T ΔS.
För ideala gaser är förändringen av en isotermisk process entropi:
AS = nR ln (V.två/ V1)
Det som gäller fallet med denna övning kvarstår:
AS = 2 mol x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K
Då kan vi få förändringen i Helmholtz energi:
ΔG = - 300K x 11,53 J / K = -3457,70 J.
Med hänsyn till att Gibbs fria energi är en funktion av temperatur och tryck G = G (T, P); bestämma variationen av G under en process där temperaturen inte ändras (isotermisk) för n mol av en monatomisk idealgas.
Som visas ovan beror förändringen i Gibbs-energi bara på temperaturförändringen T och volymen V, så en oändlig variation av den beräknas enligt:
dG = -SdT + VdP
Men om det är en process där temperaturen är konstant då dF = + VdP, så en ändlig tryckvariation ΔP leder till en förändring av Gibbs-energin som ges av:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = + n R T ln (AP)
Med den ideala gasekvationen:
P V = n R T
Under en isotermisk process inträffar det att:
d (P V) = P dV + V dP = 0
Det är:
dP / P = - dV / V.
Så resultatet ovan kan skrivas som en funktion av volymvariationen AV:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = - ∫ (n R T) dV / V = -n R T ln (AV)
Med tanke på följande kemiska reaktion:
Ntvå0 (g) + (3/2) Otvå (g) ↔️ 2NOtvå (g) vid temperatur T = 298 K
Hitta variationen i Gibbs fria energi och, med hjälp av det erhållna resultatet, ange om det är en spontan process eller inte.
Här är stegen:
- Steg ett: Enthalpies of Reaction
ΔHr = 2 * ΔH (NOtvå (g)) - Ah (NtvåO (g)) = 2 * 33,2-81,6 = -15,2 kJ / mol
- Andra steget: reaktionsentropi variation
ΔSr = 2 * S (NOtvå (g)) - S (Ntvå0 (g)) - (3/2) S (Otvå (g)) = 2 * 240,1 - 220,1 - 1,5 * 205,2 = -47,7 J / (mol * K).
- Tredje steget: variation i Gibbs-funktionen
Detta värde bestämmer balansen mellan den minskande energin och den ökande entropin för att veta om reaktionen äntligen är spontan eller inte.
ΔGr = ΔHr - T ΔSr = -15,2 -298 * (- 47,7) = -985,4 J / mol
Eftersom det är en negativ variation av Gibbs-energin kan man dra slutsatsen att det är en spontan reaktion vid temperaturen 298 K = 25 ºC.
Ingen har kommenterat den här artikeln än.