
Potentiella energiegenskaper, typer, beräkning och exempel
De potentiell energi Det är den energi som kropparna besitter på grund av sin konfiguration. När objekt samverkar finns det krafter mellan dem som kan utföra arbete, och denna förmåga att utföra arbete, som är lagrad i deras disposition, kan översättas till energi..
Till exempel har människor utnyttjat vattenfalls potentiella energi sedan urminnes tider, först genom spinnverk och sedan vid vattenkraftverk..

Å andra sidan har många material en anmärkningsvärd förmåga att utföra arbete genom att deformera och sedan återgå till sin ursprungliga storlek. Och under andra omständigheter tillåter arrangemanget av den elektriska laddningen lagring av elektrisk potentiell energi, som till exempel i en kondensator.
Potentiell energi erbjuder många möjligheter att omvandlas till andra former av användbar energi, därav vikten av att känna till lagarna som styr den..
Artikelindex
- 1 Ursprung av potentiell energi
- 2 Typer av potentiell energi
- 2.1 Gravitationspotentialenergi
- 2.2 Elastisk potentialenergi
- 2.3 Elektrostatisk potentialenergi
- 2.4 Kärnpotentialenergi
- 2.5 Kemisk potentiell energi
- 3 Exempel på potentiell energi
- 4 Beräkning av potentiell energi
- 4.1 Beräkning av gravitationspotentialenergi
- 4.2 Beräkning av elastisk potentialenergi
- 4.3 Beräkning av elektrostatisk potentialenergi
- 5 Övningar lösta
- 5.1 - Övning 1: en fjäder som sträcker sig
- 5.2 - Övning 2: konservativa och icke-konservativa krafter
- 6 Referenser
Ursprung av potentiell energi
Ett objekts potentiella energi har sitt ursprung i de krafter som påverkar det. Potentiell energi är dock en skalär storlek, medan krafterna är vektor. För att specificera den potentiella energin räcker det därför att ange dess numeriska värde och de valda enheterna.
En annan viktig egenskap är den typ av kraft som potentiell energi kan lagras med, eftersom inte varje kraft har denna dygd. Endast konservativa krafter lagrar potentiell energi i de system som de verkar på.
En konservativ kraft är en för vilken arbetet inte beror på den väg som objektet följer, utan bara på startpunkten och ankomstpunkten. Kraften som driver det fallande vattnet är tyngdkraften, som är en konservativ kraft.
Å andra sidan har elastiska och elektrostatiska krafter också denna kvalitet, därför är det potentiell energi förknippat med dem..
Krafter som inte uppfyller ovannämnda krav kallas icke-konservativa; exempel på dem är i friktion och luftmotstånd.
Typer av potentiell energi
Eftersom potentiell energi alltid härrör från konservativa krafter som de som redan nämnts, talar vi om gravitationell potentiell energi, elastisk potentiell energi, elektrostatisk potentiell energi, kärnpotentialenergi och kemisk potentiell energi..
Potentiell gravitationsenergi
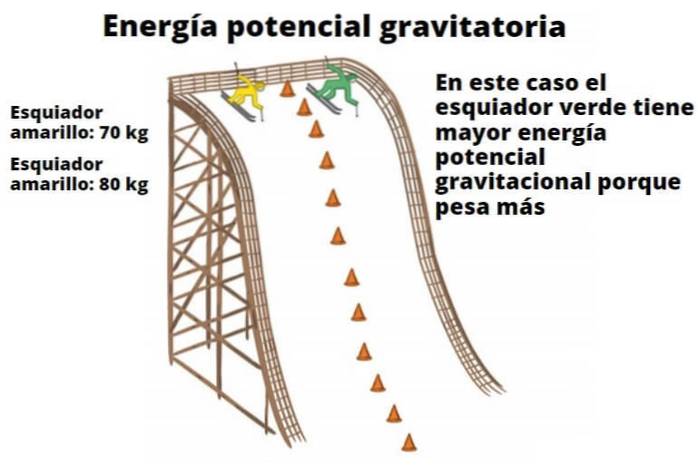
Varje objekt har potentiell energi som en funktion av dess höjd från marken. Detta till synes enkla faktum illustrerar varför fallande vatten kan driva turbiner och så småningom omvandlas till elektrisk energi. Skidåkarexemplet som visas här visar också förhållandet mellan vikt och höjd till gravitationspotentialenergi.
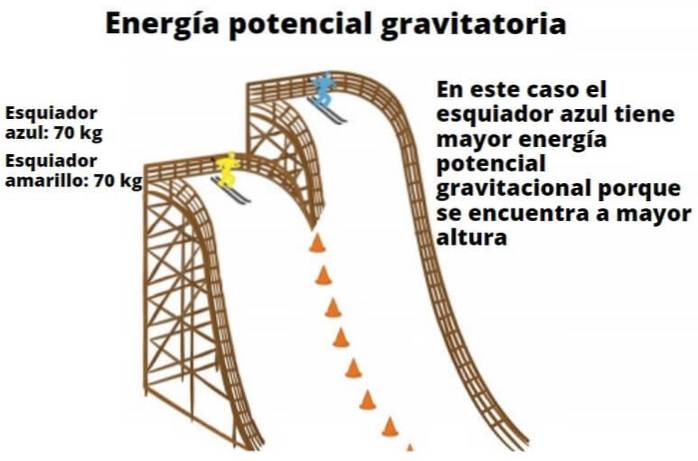
Ett annat exempel är en berg-och dalbana som har högre potentialenergi när den befinner sig i en viss höjd över marken. När den väl har nått marknivån är höjden lika med noll och all dess potentiella energi har omvandlats till kinetisk energi (rörelseenergi).
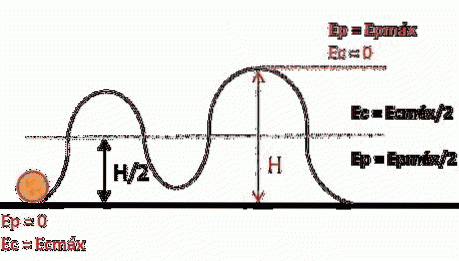
Elastisk potentialenergi
Föremål som fjädrar, bågar, armbågar och gummiband kan lagra elastisk potentialenergi..

Elastiken hos en kropp eller ett material beskrivs av Hookes lag (upp till vissa gränser), som säger att kraften som kan utövas när den komprimeras eller sträcks är proportionell mot dess deformation.
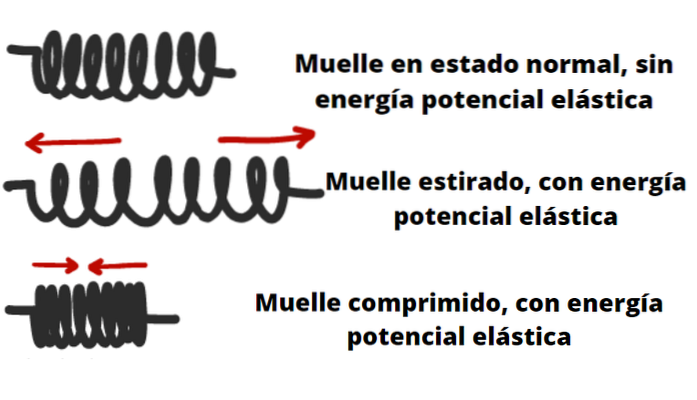
Till exempel i händelse av en fjäder eller fjäder betyder det att ju mer den krymper eller sträcker sig, desto större kraft kan den utöva på ett föremål placerat i ena änden..
Elektrostatisk potentialenergi
Det är energin som elektriska laddningar har på grund av sin konfiguration. Elektriska laddningar med samma tecken avvisar varandra, så för att placera ett par positiva - eller negativa - laddningar i en viss position måste en extern agent göra arbete. Annars tenderar de att separera.
Detta arbete lagras på det sätt som lasterna lokaliserades. Ju närmare laddningarna för samma skylt är, desto högre potentiell energi kommer konfigurationen att ha. Motsatsen händer när det gäller massor av olika tecken; hur de lockar, ju närmare de är, desto mindre potential har de.
Kärnpotentialenergi
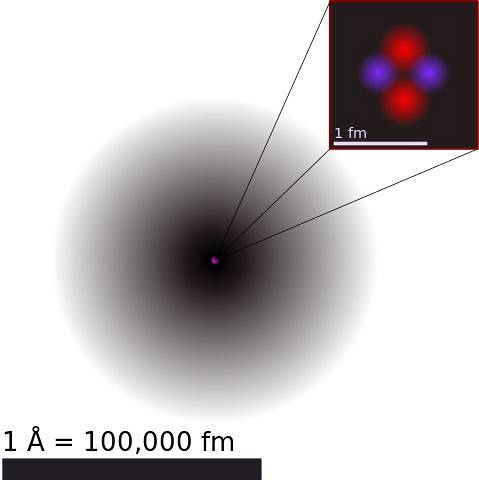
Atomkärnan består av protoner och neutroner, generiskt kallade nukleoner. De förstnämnda har en positiv elektrisk laddning och de senare är neutrala..
Eftersom de är agglomererade i ett litet utrymme bortom fantasin, och att veta att laddningar av samma tecken stöter varandra, undrar man hur atomkärnan förblir sammanhängande.
Svaret ligger i andra krafter än elektrostatisk avstötning, typiska för kärnan, såsom den starka kärninteraktionen och den svaga kärnkraftsinteraktionen. Dessa är mycket starka krafter, som långt överstiger den elektrostatiska kraften.
Kemisk potentiell energi
Denna form av potentiell energi kommer från hur ämnets atomer och molekyler är ordnade enligt de olika typerna av kemiska bindningar..
När en kemisk reaktion inträffar kan denna energi omvandlas till andra typer, till exempel med hjälp av ett batteri eller ett elektrisk batteri.
Exempel på potentiell energi
Potentiell energi finns i det dagliga livet på många sätt. Att observera dess effekter är lika enkelt som att placera något föremål i en viss höjd och vara säker på att det kan rulla eller falla när som helst.
Här är några manifestationer av de typer av potentiell energi som beskrivits tidigare:
-Berg-och dalbanor
-Bilar eller bollar som rullar nedför

-Bågar och pilar
-Elektriska batterier
-En klockpendel

-Gunga på en gunga
-Hoppa på en studsmatta
-Använd en infällbar penna.
Se: potentiella energiexempel.
Beräkning av potentiell energi
Den potentiella energin beror på kraftens arbete och detta beror i sin tur inte på banan, så det kan sägas att:
-Om A och B är två punkter, fungerar WAB nödvändigt att gå från A till B är lika med det arbete som krävs för att gå från B till A. Därför: WAB = WBA, så:
WAB + WBA = 0
-Och om två olika banor 1 och 2 försöks förenas med nämnda punkter A och B, är det arbete som utförts i båda fallen också detsamma:
W1 = Wtvå.
I båda fallen upplever objektet en förändring av potentiell energi:
Förändring = Slutlig potentiell energi - Initial potentiell energi
UU = Uslutlig - ELLERförsta = UB - ELLERTILL
Tja, objektets potentiella energi definieras som det negativa av det arbete som utförts av den (konservativa) kraften:
AU = -WAB
Men eftersom arbete definieras av denna integral:


Observera att enheterna av potentiell energi är desamma som för arbetet. I SI International System är enheten joule, som förkortas J och motsvarar 1 newton x meter, av den engelska fysikern James Joule (1818-1889).
Andra enheter för energi inkluderar cgs erg, pund-kraft x fot, BTU (British Thermal Unit), kalorier och kilowattimmar.
Låt oss se nedan några speciella fall av hur man beräknar potentiell energi.
Beräkning av gravitationspotentialenergi
I närheten av jordytan pekar tyngdkraften vertikalt nedåt och dess storlek ges av ekvationen Vikt = massa x gravitation.
Betecknar den vertikala axeln med bokstaven "y" och tilldelar enhetsvektorn till denna riktning j, positivt upp och negativt ner, förändringen i potentiell energi när en kropp rör sig från y = yTILL fram tills y = yB det är:

U (y) = mgy
Beräkning av elastisk potentialenergi
Hookes lag säger oss att kraften är proportionell mot deformationen:
F = -k.x
Här x är deformationen och k är en egenkonstant av fjädern, vilket indikerar hur styv den är. Genom detta uttryck beräknas den elastiska potentialenergin med hänsyn till det i är enhetsvektorn i horisontell riktning:

U (x) = ½ kxtvå
Beräkning av elektrostatisk potentialenergi
När du har en punktladdning Q, producerar den ett elektriskt fält som uppfattar en annan punktladdning Vad, och att det fungerar på det när det flyttas från en position till en annan i mitten av fältet. Den elektrostatiska kraften mellan tvåpunktsladdningar har en radiell riktning, symboliserad av enhetsvektorn r:



Lösta övningar
- Övning 1: en fjäder som sträcker sig
En fjäder vars konstant är k = 10,0 N / cm sträcker sig initialt 1,00 cm från dess jämviktslängd. Du ombeds beräkna den extra energi som krävs för att sträcka fjädern upp till 5,00 cm över dess jämviktslängd..
Lösning
Genom att direkt ersätta x = 1,00 cm i ekvationen för U (x) får vi N.cm, men centimeterna måste omvandlas till meter för att erhålla energin i joule:
U (1) = 0,5 x 10,0 N / cm x (1,00 cm)två = 5 N. cm = 0,05 J; U (5) = 0,5 x 10,0 N / cm x (5,00 cm)två = 125 N.cm = 1,25 J
Därför är den efterfrågade energidifferensen 1,25 - 0,05 J = 1,20 J.
- Övning 2: konservativa och icke-konservativa krafter
Ett litet block frigörs från vila från punkt A för att glida längs den friktionsfria böjda rampen till punkt B. Därifrån går det in i en lång grov horisontell yta med en dynamisk friktionskoefficient μk = 0,2. Hitta hur långt från punkt B det stannar, förutsatt att hTILL= 3m.

Lösning
När blocket är på en höjd hTILL Med avseende på marken har den gravitationspotentialenergi på grund av dess höjd. När den potentiella energin frigörs omvandlas den gradvis till kinetisk energi, och när den glider nedför den släta krökta rampen ökar hastigheten..
Under vägen från A till B kan ekvationerna med jämnt varierad rätlinjig rörelse inte tillämpas. Även om tyngdkraften är ansvarig för blockets rörelse är rörelsen den upplever mer komplex, eftersom banan inte är rätlinjig.
Energibesparing i väg AB
Eftersom tyngdkraften är en konservativ kraft och det inte finns någon friktion på rampen kan du använda bevarande av mekanisk energi för att hitta hastigheten i slutet av rampen:
Mekanisk energi i A = Mekanisk energi i B
m.g.hTILL + ½ m.vTILLtvå = m.g.hB + ½ m.vBtvå
Uttrycket förenklas genom att notera att massan visas i varje term. Det frigörs från vila vTILL = 0. Och hB är på marknivå, hB = 0. Med dessa förenklingar minskar uttrycket till:
vBtvå = ghTILL
Arbetet utförs genom att gnugga i avsnitt BC
Nu börjar blocket sin resa i den grova sektionen med denna hastighet och slutar slutligen vid punkt C. Därför vC = 0. Mekanisk energi bevaras inte längre, eftersom friktion är en avledande kraft, som har gjort arbete på blocket från:
WRör = - friktionskraft x rest sträcka
Detta arbete har ett negativt tecken, eftersom den kinetiska friktionen saktar objektet motsatt dess rörelse. Storleken på den kinetiska friktionen Fk det är:
Fk = μk .N
Där N är den normala kraftens storlek. Den normala kraften utövas av ytan på blocket, och eftersom ytan är helt horisontell balanserar den vikten P = mg, därför är normalens storlek:
N = mg
Som leder till:
Fk = μk .mg
Arbetet som Fk gör om blocket är: Wk = - fk .D = - μk .mg D..
Beräkning av förändring av mekanisk energi
Detta arbete motsvarar förändring i mekanisk energi, beräknat så här:
Mekanisk energi i C - Mekanisk energi i B =
AEm = (UC +KC) - (ELLERB + KB) = - μk .mg D.
I denna ekvation finns det några termer som försvinner: KC = 0, eftersom blocket stannar vid C och U försvinner ocksåC = UB, eftersom dessa punkter ligger på marknivå. Förenklingen resulterar i:
- KB = - μk .m.g. D.
½ m.vBtvå = μk .m.g. D.
Massan avbryts igen och D kan erhållas enligt följande:
D = (½ vBtvå) / (μk . g) = (½ vBtvå) / (μk . g) = (½g.hTILL) / (μk . g) = (½hTILL) / μk = 0,5 x 3 m / 0,2 = 7,5 m
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 2. Dynamik. Redigerad av Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Utg. Volym 1-2.


Ingen har kommenterat den här artikeln än.