
Beskrivande statistikhistoria, egenskaper, exempel, begrepp
De Beskrivande statistik är den gren av statistik som ansvarar för att samla in och organisera information om beteendet hos system med många element, allmänt känt under namnet befolkning.
För att göra detta använder den numeriska och grafiska tekniker, genom vilka den presenterar information, utan att göra förutsägelser eller slutsatser om befolkningen från vilken den kommer..

Artikelindex
- 1 Historia
- 1.1 Forntida ålder
- 1.2 Renässans
- 1.3 Modern tid
- 2 Kännetecken för beskrivande statistik
- 3 Vad är beskrivande statistik för?
- 3.1 Ekonomi
- 3.2 Fysik och mekanik
- 3.3 Medicin
- 3.4 Näring
- 4 Exempel på beskrivande statistik
- 4.1 Exempel 1
- 4.2 Exempel 2
- 4.3 Exempel 3
- 5 Grundläggande begrepp för beskrivande statistik
- 5.1 Befolkning
- 5.2 Prov
- 5.3 Variabel
- 5.4 Mått på central tendens
- 5.5 Dispersionsmätningar
- 6 Intressanta ämnen
- 7 Referenser
Berättelse
Gammal ålder
Statistik har sitt ursprung i det mänskliga behovet av att organisera den information som är nödvändig för dess överlevnad och välbefinnande, samt att förutse de händelser som påverkar den. Antikens stora civilisationer lämnade register över bosättare, skatter som samlats in, antal skördar och arméernas storlek.
Ramses II (1279-1213 f.Kr.) beordrade till exempel en folkräkning av länder och invånare i Egypten, som då hade cirka 2 miljoner invånare.
På samma sätt berättar Bibeln att Mose genomförde en folkräkning för att ta reda på hur många soldater de tolv stammarna i Israel hade.
Även i det antika Grekland räknades människor och resurser. Romarna, som var anmärkningsvärda för sin höga organisation, registrerade regelbundet befolkningen och utarbetade folkräkningar vart femte år, inklusive territorier och resurser..
Renässans
Efter Roms nedgång var viktiga statistiska register knappa fram till renässansens ankomst, då statistiken återuppstod som ett hjälpmedel i beslutsfattandet.
I slutet av 1600-talet föddes sannolikhetsteorin, resultatet av människors benägenhet för hasardspel, vilket gav statistik den matematiska noggrannhet som gjorde den till en vetenskap i sig själv.
Modern tid
En ny impuls kom med teorin om fel och minsta kvadrater på 1800-talet, som följdes av metoden för korrelation mellan variabler, för att kvantitativt bedöma förhållandet mellan dem..
Fram till slut, under 1900-talet, spridte statistiken till varje gren av vetenskap och teknik som ett oumbärligt verktyg för att lösa problem..
Beskrivande statistiska egenskaper
Beskrivande statistik kännetecknas av:
- Organisera den insamlade informationen i form av data och grafer. Diagrammen kan vara olika: bland annat histogram, frekvenspolygoner, cirkelformade diagram..
- Distribuera data i frekvensområden för att underlätta dess hantering. Använd aritmetik för att hitta de mest representativa värdena för data, genom mått på central tendens, samt analysera deras spridning.
- Bestäm formen på fördelningarna, deras symmetri, om de är centrerade eller sneda och om de är spetsiga eller snarare tillplattade.
Vad är beskrivande statistik för?
Närhelst data behöver samlas in, organiseras och presenteras är beskrivande statistik viktigt inom vetenskapsområden som behandlar många element och kvantiteter, liksom i mycket av mänsklig verksamhet: ekonomi, politik, hälsa, sport och mer..
Här är några exempel:
Ekonomi
Beskrivande statistik handlar om att konsekvent registrera och organisera data om befolkningar och deras åldrar, inkomst, investeringar, inkomster och utgifter. På detta sätt planerar regeringar och institutioner förbättringar och investerar resurser på lämpligt sätt..
Med hjälp övervakas inköp, försäljning, retur och effektivitet av tjänsterna. Av denna anledning är statistik avgörande för beslutsfattandet.
Fysik och mekanik
Fysik och mekanik använder statistik för att studera kontinuerliga medier, som består av ett stort antal partiklar, såsom atomer och molekyler. Det visar sig att det inte går att spåra var och en separat..
Men när man studerar systemets globala beteende (till exempel en del gas) ur makroskopisk synvinkel är det möjligt att hitta medelvärden och definiera makroskopiska variabler för att känna till deras egenskaper. Ett exempel på detta är den kinetiska teorin om gaser.
Medicin
Det är ett viktigt verktyg vid övervakning av sjukdomar, från deras ursprung och under deras utveckling, liksom effektiviteten av behandlingar.
Statistik som beskriver sjuklighet, bota, inkubations- eller utvecklingstider för en sjukdom, åldern vid vilken det vanligtvis förekommer och liknande data är nödvändiga när man utformar de mest effektiva behandlingarna..
Näring
En av de många tillämpningarna av beskrivande statistik är att registrera och beställa data om matkonsumtion i olika populationer: dess kvantitet, kvalitet och vilken som konsumeras mest, bland många andra observationer som intresserar experter..
Beskrivande statistikexempel
Här är några exempel som illustrerar hur användbara beskrivande statistikverktyg är för att fatta beslut:
Exempel 1

Utbildningsmyndigheterna i ett land planerar institutionella förbättringar. Antag att du ska implementera ett nytt skolmatsystem.
För detta är det nödvändigt att ha uppgifter om studentpopulationen, till exempel antalet elever per klass, deras ålder, kön, längd, vikt och socioekonomiska status. Denna information presenteras sedan i form av tabeller och grafer..
Exempel 2
För att hålla reda på det lokala fotbollslaget och göra nya signeringar håller cheferna reda på antalet spelade, vunna, oavgjorda och förlorade spel, samt antalet mål, målskyttar och hur de lyckades göra mål: frispark, halv domstol, påföljder, med vänster eller höger ben, bland annat detaljer.
Exempel 3
En glassbar har flera smaker av glass och vill förbättra sin försäljning, därför gör ägarna en studie där de räknar antalet kunder, de delar upp dem i grupper efter kön och åldersintervall.
I den här studien registreras till exempel favoritglassmaken och den bästsäljande presentationen. Och med de insamlade uppgifterna planerar de inköp av smaker och behållare och tillbehör som är nödvändiga för beredningen..
Grundläggande beskrivande statistik
Dessa grundläggande begrepp är nödvändiga för att tillämpa statistiska tekniker, låt oss se:
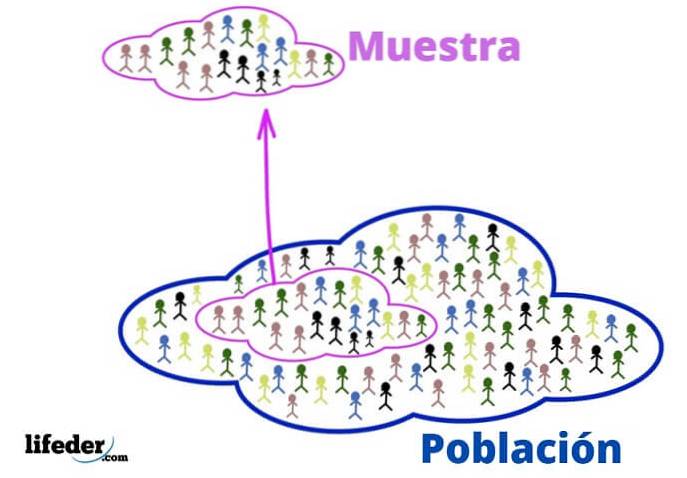
Befolkning
I det statistiska sammanhanget hänvisar befolkningen till det universum eller den grupp som informationen kommer från.
De handlar inte alltid om människor, eftersom de kan vara grupper av djur, växter eller föremål som bilar, atomer, molekyler och till och med händelser och idéer..
Show
När befolkningen är mycket stor dras ett representativt urval från den och analyseras utan att förlora relevant information..
Det kan väljas slumpmässigt eller enligt vissa kriterier som tidigare fastställts av analytikern. Fördelen är att det är mycket mer hanterbart att vara en delmängd av befolkningen.
Variabel
Det hänvisar till den uppsättning värden som en viss egenskap hos befolkningen kan ta. En studie kan innehålla flera variabler, såsom ålder, kön, vikt, akademisk nivå, civilstånd, inkomst, temperatur, färg, tid och många fler.
Variablerna kan ha olika karaktär, så det finns kriterier för att klassificera dem och ge dem den mest lämpliga behandlingen.
Kategoriska variabler och numeriska variabler
Beroende på hur de mäts kan variablerna vara:
-Kategorisk
-Numerisk
Kategoriska variabler, även kallade kvalitativ, representerar egenskaper som en persons civilstånd, som kan vara ensamstående, gift, frånskild eller änka.
Istället numeriska variabler eller kvantitativ, kan mätas, såsom ålder, tid, vikt, inkomst och mer.
Diskreta variabler och kontinuerliga variabler
Diskreta variabler tar bara diskreta värden, som namnet antyder. Exempel på dem är antalet barn i en familj, hur många ämnen som är på en viss kurs och antalet bilar på en parkeringsplats.
Dessa variabler tar inte alltid heltalsvärden, eftersom det också finns bråkdelar.
Å andra sidan medger kontinuerliga variabler oändliga värden inom ett visst intervall, såsom en persons vikt, blodets pH, tiden för en telefonkonsultation och diametern på fotbollar..
Mått på centrala tendenser
De ger en uppfattning om den allmänna trenden följt av data. Vi kommer att nämna de tre mest använda centrala åtgärderna:
-Halv
-Median
-mode
Halv
Motsvarar genomsnittet av värdena. Det beräknas genom att lägga till alla observationer och dividera med det totala antalet:

mode
Det är det värde som upprepas mest i en datamängd, det mest eller det mest frekventa, eftersom det i en distribution kan finnas mer än ett läge.
Median
När du sorterar en uppsättning data är medianen det centrala värdet för dem alla.
Åtgärder för spridning
De pekar på datavariabiliteten och ger en uppfattning om hur långt eller spridda de är från de centrala måtten. De mest använda är:
Rang
Det är skillnaden mellan det största värdet xM och den minsta xm från en datamängd:
Rank = xM - xm
Variation
Mäter hur långt data ligger från medelvärdet. För att göra detta görs ett genomsnitt, men med skillnaderna mellan vilket värde som helst xi och medelvärdet, kvadrera för att förhindra dem från att avbryta varandra. Det betecknas vanligtvis med den grekiska bokstaven σ i kvadrat, eller med stvå:

Variansen har inte samma enheter som data, så standardavvikelsen definieras som kvadratroten av variansen och betecknas som σ eller s:

Istället för att ta hänsyn till varje data individuellt är det att föredra att gruppera dem i intervall, vilket underlättar arbetet, särskilt om det finns många värden. När man till exempel arbetar med barn i en skola kan de grupperas i åldersintervaller: 0 till 6 år, 6 till 12 år och 12 till 18 år.
Diagram
De är ett utmärkt sätt att snabbt se distributionen av data och innehåller all information som samlats in i tabellerna och tabellerna, men mycket billigare.
Det finns ett stort utbud av dem: med staplar, linjär, cirkulär, stam och blad, histogram, frekvenspolygoner och piktogram. Exempel på statistiska diagram visas i figur 3..
Teman av intresse
Grenar av statistik.
Statistiska variabler.
Befolkning och prov.
Inferentiell statistik.
Referenser
- Faraldo, P. Statistik och forskningsmetodik. Återställd från: eio.usc.es.
- Fernández, S. 2002. Beskrivande statistik. 2: a. Utgåva. ESIC Ledare. Återställd från: Google Books.
- Statistikhistoria. Återställd från: eumed.net.
- Ibañez, s. 2010. Matematik II. Kompetensmetod. Cengage Learning.
- Monroy, S. 2008. Beskrivande statistik. 1: a Utgåva. National Polytechnic Institute of Mexico.
- Universumsformler. Beskrivande statistik. Återställd från: universoformulas.com.



Ingen har kommenterat den här artikeln än.