
Grundläggande trigonometriska funktioner, i det kartesiska planet, exempel, träning
De trigonometriska funktioner av verklig variabel motsvarar vilken vinkel som helst (uttryckt i radianer), ett trigonometriskt förhållande, som kan vara sinus, cosinus, tangent, cotangent, secant och cosecant.
På detta sätt har vi de sex trigonometriska funktionerna: sinus, cosinus, tangent, cosecant, secant och cotangent..
De trigonometriska funktionerna för vinklar mellan 0 och 2π definieras med hjälp av enhetscirkeln, med radie 1 och vars centrum sammanfaller med det ursprung från det kartesiska koordinatsystemet: punkten (0,0).
Vi kan hitta vilken punkt som helst av koordinaterna (x, y) på denna omkrets.
Segmentet som förenar ursprunget med P, tillsammans med respektive segment som förenar projektionerna av P på koordinataxlarna, utgör en höger triangel, vars trigonometriska förhållanden är kända som förhållandena mellan sidorna av triangeln. A) Ja:
- sin θ = motsatt ben / hypotenus
- cos θ = intilliggande ben / hypotenus
- tg θ = motsatt ben / intilliggande ben
Och nu skälen som är motsatsen till de tidigare:
- sek θ = hypotenus / angränsande ben
- cosec θ = hypotenus / motsatt ben
- ctg θ = angränsande ben / motsatt ben
I enhetscirkeln är hypotenusen i vilken triangel som helst lika med 1 och benen är värda x och y, så:
sin θ = y
cos θ = x
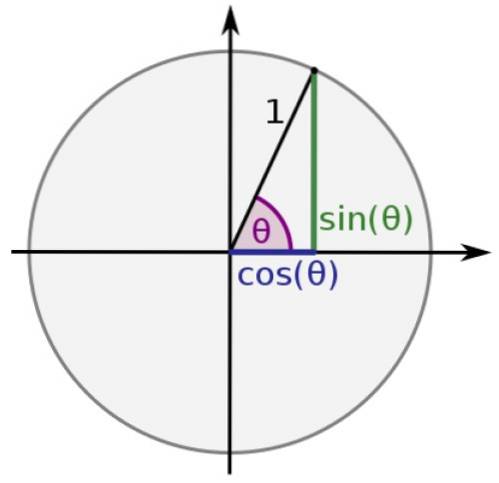
På detta sätt förvärvar sinus- och cosinusfunktionerna alltid värden mellan -1 och 1, medan resten:
tg θ = y / x
cosec θ = 1 / y
sek θ = 1 / x
De definieras inte när x eller Y värt 0.
Artikelindex
- 1 Trigonometriska funktioner i det kartesiska planet
- 1.1 Funktion f (x) = sin x
- 1.2 Funktion f (x) = cos x
- 1.3 Diskontinuerliga trigonometriska funktioner
- 2 Övningen löst
- 2.1 Lösning
- 3 Referenser
Trigonometriska funktioner på det kartesiska planet
Som vi kommer att se nedan kännetecknas trigonometriska funktioner av att vara periodiska. Därför är de inte bindande, utom i en begränsad domän..
Funktion f (x) = sin x
Från och med den trigonometriska cirkeln vid punkten P (1,0) är vinkeln 0 radianer. Sedan roterar radien moturs och sin x-funktionen växer gradvis tills den når π / 2 radianer (90º), vilket motsvarar ungefär 1571 radianer..
Där når det värdet y = 1 och minskar sedan tills det når noll i π radianer (180 °). Senare minskar det ännu mer, eftersom värdet blir negativt tills det når -1 när vinkeln är 3π / 2 radianer (270 °).
Slutligen ökar den igen tills den återgår till noll i 360 °, där allt börjar igen. Detta gör att y = sin x a periodisk funktion för period 2π, därför är sinusfunktionen inte bijektiv.
Grafen är också symmetrisk med avseende på punkten (0,0), därför är funktionen udda.
Då grafen för y = sin x:
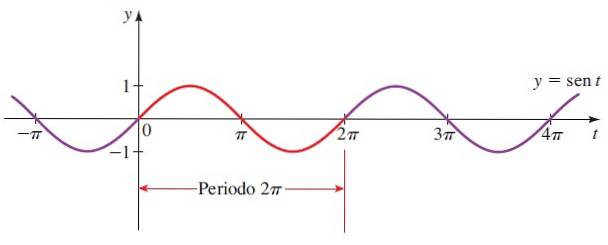
Avsnittet i rött är den första perioden. Negativa vinklar beaktas också, eftersom trigonometrisk cirkels radie kan rotera medurs.
Sin domän x = Alla verkliga.
Syndens räckvidd eller väg x = [-1,1]
Funktion f (x) = cos x
Vid punkten P (1,0) är cosinusfunktionen värd 1 och därifrån minskar den och når 0 när vinkeln är π / 2. Den fortsätter att minska och tar negativa värden tills den når -1 i vinkeln π.
Sedan börjar den gradvis öka tills den når 0 i 3π / 2 och återgår till värdet 1 när radien har gjort en total varv. Därifrån upprepar cykeln sig själv, eftersom cos x är periodisk och också är jämn (symmetrisk runt den vertikala axeln).
Formen för cosinusfunktionen är densamma som sinusfunktionen, förutom att de förskjuts π / 2 i förhållande till varandra..
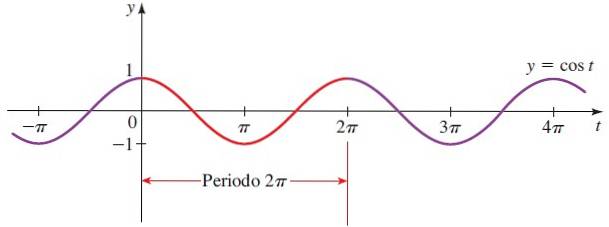
Domän för cos x = Alla verkliga.
Cos x räckvidd eller resa = [-1,1]
Diskontinuerliga trigonometriska funktioner
Funktionerna tg x, ctg x, sec x och cosec x är diskontinuerliga, eftersom de är kvoter mellan sinus och cosinus eller det inversa. Eftersom dessa är värda 0 i vissa vinklar gör de funktionen diskontinuerlig när de visas i nämnaren.
Och eftersom sinus och cosinus är periodiska funktioner är funktionerna tg x, ctg x, sec x, cosec x också periodiska..
Tangentfunktion f (x) = tg x
För tangentfunktionen är diskontinuitetsvärdena: ± π / 2, ± 3π / 2, ± 5π / 2 ... Där tar funktionen mycket stora eller mycket små värden. I allmänhet händer detta för alla multiplar av π av formen (2n + 1) π / 2, både positiva och negativa, med n = 0, 1, 2 ...
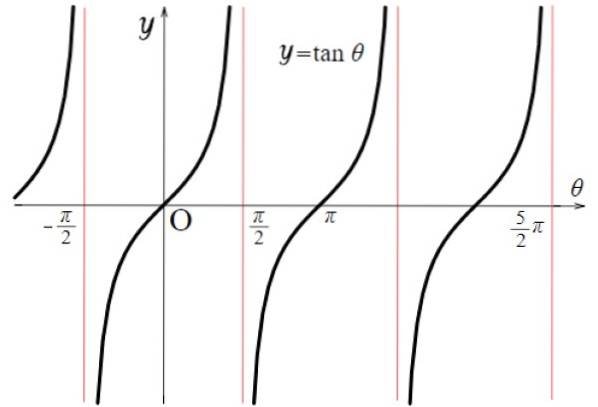
Därför:
Tg x domän: D = x ∈ R / x ^ (2n + 1) π / 2; n ∈ Z
Tg x räckvidd eller resa: Alla riktiga.
Observera att funktionen f (x) = tg x upprepas mellan - π / 2 och + π / 2, därför är dess period π. Dessutom är det symmetriskt med avseende på ursprunget.
Kotangentfunktion f (x) = ctg x
För denna funktion förekommer diskontinuitetsvärdena vid 0, ± π, ± 2π ..., det vill säga heltalsmultiplarna av π.
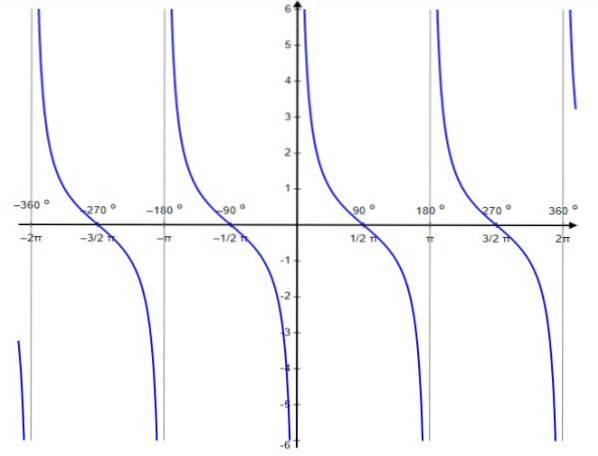
Liksom tangentfunktionen är cotangentfunktionen periodisk av period π. För henne är det sant att:
Ctg x domän: D = x ∈ R / x ≠ n π; n ∈ Z
Ctg x räckvidd eller resa: Allt riktigt.
Sekantfunktion f (x) = sek x
Sec x-funktionen har diskontinuitetspunkter vid ± π / 2, ± 3π / 2, ± 5π / 2…, där cos x = 0. Det är också periodiskt med period π och det observeras också från diagrammet att funktionen aldrig tar värden i intervallet (-1,1)
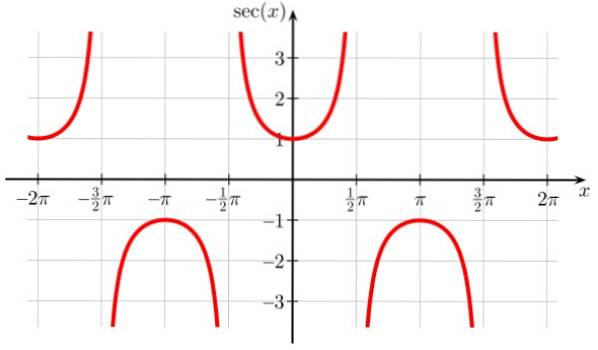
Domän för sek x: D = x ∈ R / x ^ (2n + 1) π / 2; n ∈ Z
Sek x räckvidd eller resa: Alla verkliga utom (-1,1)
Cosecant-funktion f (x) = cosec x
Det liknar sekantfunktionen, även om den flyttas åt höger, därför är diskontinuitetspunkterna 0, ± π, ± 2π och alla helmultiplar av π. Det är också periodiskt.
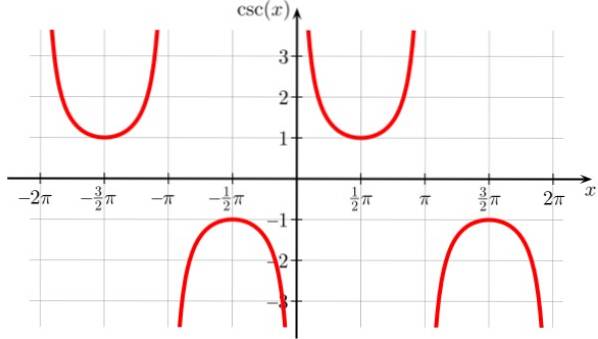
Cosec Domain X: D = x ∈ R / x ≠ n π; n ∈ Z
Skördeområde eller väg x: Alla verkliga utom (-1,1)
Övningen löst
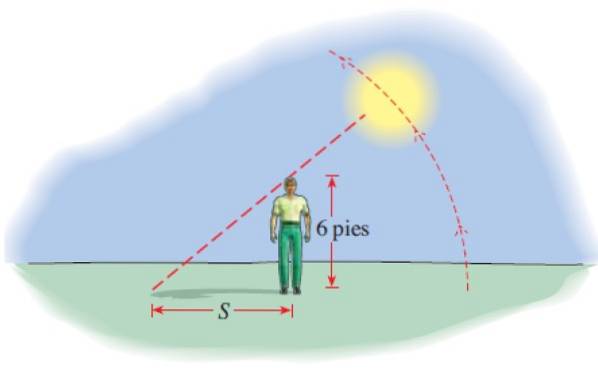
En 6 fot lång man kastar en skugga S vars längd ges av:
S (t) = 6 │cot (π.t / 12) │
Med S i fot och t antalet timmar sedan 6 AM. Hur lång är skuggan 08.00, 12.00, 14.00 och 17.45?
Lösning
Vi måste utvärdera funktionen för vart och ett av de angivna värdena, notera att den måste ta det absoluta värdet, eftersom skuggans längd är positiv:
-Klockan 8 har två timmar gått från 06:00, därför är t = 2 och S (t):
S (2) = 6 │cot (π.2 / 12) │ft = 6 │cot (π / 6) │ft = 10,39 fot.
-När det är 12 N har t = 6 timmar gått, därför:
S (6) = 6 │cot (π.6 / 12) │ft = 6 │cot (π / 2) │ft = 0 fot. (Vid den tiden faller solen vertikalt på personens huvud).
-Kl 14.00 t = åtta timmar gått:
S (8) = 6 │cot (π.8 / 12) │ft = 6 │cot (2π / 3) │ft = 3,46 fot.
-När klockan 17.45 har 11.75 timmar redan gått sedan 06.00, så:
S (11,75) = 6 │ barnsäng (π x 11,75 / 12) │ fötter = 91,54 fot. Vid denna timme blir skuggorna längre.
Kan läsaren beräkna tiden när personens skugga är lika med hans höjd??
Referenser
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Figuera, J. 1999. Matematik. 1: a Diversifierad. Bolivarian Collegiate Editions.
- Hoffman, J. Selection of Mathematics Topics. Volym 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Zill, D. 1984. Algebra och trigonometri. Mcgraw hill.



Ingen har kommenterat den här artikeln än.