
Heptadekagons egenskaper, diagonaler, omkrets, area

De heptadecagon är en vanlig polygon med 17 sidor och 17 hörn. Dess konstruktion kan göras i euklidisk stil, det vill säga med endast linjalen och kompassen. Det var det stora matematiska geniet Carl Friedrich Gauss (1777-1855), knappt 18 år gammalt, som hittade förfarandet för dess konstruktion 1796.
Tydligen var Gauss alltid mycket benägen till denna geometriska figur, i en sådan utsträckning att han från den dag han upptäckte dess konstruktion bestämde sig för att vara matematiker. Det sägs också att han ville att heptadekagonen skulle graveras på hans gravsten.

Gauss hittade också formeln för att bestämma vilka vanliga polygoner som har möjligheten att konstrueras med linjal och kompass, eftersom vissa inte har exakt euklidisk konstruktion.
Artikelindex
- 1 Egenskaper hos heptadecagon
- 2 diagonaler och omkrets
- 2.1 Heptadekagons omkrets
- 3 Område
- 3.1 Området ges åt sidan
- 3.2 Område givet radie
- 4 Exempel
- 4.1 Exempel 1
- 4.2 Exempel 2
- 5 Referenser
Heptadecagonens egenskaper
När det gäller dess egenskaper, som alla polygoner, är summan av dess inre vinklar viktig. I en vanlig polygon av n sidor ges summan av:
Sa (n) = (n -2) * 180 °.
För heptadecagon antalet sidor n det är 17, vilket innebär att summan av dess inre vinklar är:
Sa (17) = (17 - 2) * 180º = 15 * 180º = 2700º.
Denna summa, uttryckt i radianer, ser ut så här:
Sa (17) = (17 - 2) * π = 15 * π = 15π
Från ovanstående formler kan man enkelt dra slutsatsen att varje inre vinkel på en heptadagon har ett exakt mått α givet av:
α = 2700º / 17 = (15/17) π radianer
Det följer att den inre vinkeln i ungefärlig form är:
α ≈ 158,824º
Diagonaler och omkrets
Diagonaler och omkrets är andra viktiga aspekter. I vilken polygon som helst är antalet diagonaler:
D = n (n - 3) / 2 och när det gäller heptadecagon, som n = 17, det är då det D = 119 diagonaler.
Å andra sidan, om längden på vardera sidan av heptadecagon är känd, så finns omkretsen av den vanliga heptadecagon helt enkelt genom att lägga till 17 gånger den längden, eller vad som motsvarar 17 gånger längden d På varje sida:
P = 17 d
Heptadekagons omkrets
Ibland är bara radien känd r av heptadecagon, så det är nödvändigt att utveckla en formel för detta fall.
För detta ändamål begreppet apotem. Apotemet är det segment som går från mitten av den vanliga polygonen till mittpunkten på ena sidan. Apotemet relativt ena sidan är vinkelrätt mot den sidan (se figur 2).
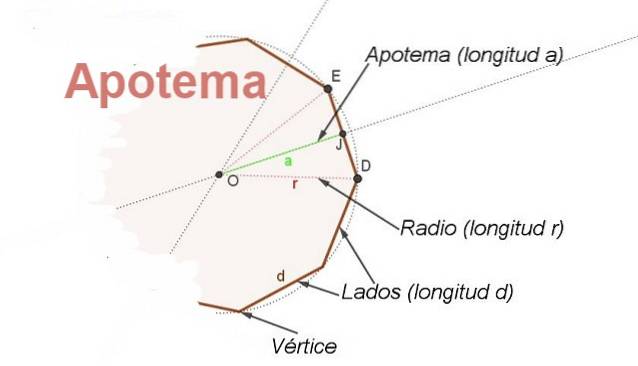
Dessutom är apotemet halvan av vinkeln med mittpunkten och sidorna på två på varandra följande hörn av polygonen, detta gör det möjligt att hitta en relation mellan radien r och sidan d.
Om det kallas β till den centrala vinkeln HIND och med hänsyn till att apotemet EGT är halvering du har EJ = d / 2 = r Sen (P / 2), från där det finns en relation för att hitta längden d på sidan av en känd polygon dess radie r och dess centrala vinkel β:
d = 2 r Sen (P / 2)
När det gäller heptadecagon β = 360º / 17 så du har:
d = 2 r Sen (180º / 17) ≈ 0,3675 r
Slutligen erhålls formeln för heptadekagons omkrets, känd sin radie:
P = 34 r Sen (180º / 17) ≈ 6,2475 r
En heptadekagons perimeter är nära omkretsen av omkretsen som omger den, men dess värde är mindre, det vill säga omkretsen av den omskrivna cirkeln är Pcir = 2π r ≈ 6,2832 r.
Område
För att bestämma området på heptadekagonen kommer vi att hänvisa till figur 2, som visar sidorna och apotemet för en vanlig polygon av n sidor. I denna figur triangeln EOD har ett område som är lika med basen d (polygonsida) gånger höjd till (polygon apothem) dividera med två:
EOD-område = (d x a) / 2
Så känt apotemet till av heptadecagon och sidan d dess område är:
Heptadekagonarea = (17/2) (d x a)
Området ges sidan
För att erhålla en formel för heptadekagons yta som känner till längden på de sjutton sidorna, är det nödvändigt att erhålla en relation mellan apotemets längd till och sidan d.
Med hänvisning till figur 2 erhålls följande trigonometriska förhållande:
Tan (β / 2) = EJ / OJ = (d / 2) / a, varelse β till den centrala vinkeln HIND. Så apotemet till kan beräknas om längden är känd d från sidan av polygonen och den centrala vinkeln β:
a = (d / 2) Cotan (P / 2)
Om detta uttryck nu ersätts med apotemet, i formeln för området för heptadecagon som erhållits i föregående avsnitt, har vi:
Heptadekagonarea = (17/4) (dtvåCotan (P / 2)
Varelse β = 360º / 17 för heptadecagon, så vi har äntligen önskad formel:
Heptadekagonarea = (17/4) (dtvå) Cotan (180º / 17)
Område med tanke på radien
I de föregående avsnitten hade en relation hittats mellan sidan d av en vanlig polygon och dess radie r, detta förhållande var följande:
d = 2 r Sen (P / 2)
Detta uttryck för d introduceras i uttrycket som erhölls i föregående avsnitt för området. Om relevanta substitutioner och förenklingar görs, erhålls formeln som gör det möjligt att beräkna heptadekagonens yta:
Heptadecagon-område = (17/2) (rtvåSen (β) = (17/2) (rtvå) Sen (360º / 17)
Ett ungefärligt uttryck för området är:
Heptadecagon-area = 3.0706 (rtvå)
Som förväntat är detta område något mindre än det område av cirkeln som avgränsar heptadagon. TILLcirk = π rtvå ≈ 3.1416 rtvå. För att vara exakt är den 2% mindre än den för sin begränsade cirkel.
Exempel
Exempel 1
Vilket värde måste radien och diametern på den begränsade omkretsen ha för en heptadagon att ha sidor på 2 cm? Hitta också värdet på omkretsen.
För att svara på frågan är det nödvändigt att komma ihåg förhållandet mellan sidan och radien hos en vanlig n-sidig polygon:
d = 2 r Sen (180º / n)
För heptadecagon n = 17, så att d = 0,3675 r, dvs heptadekagons radie är r = 2 cm / 0,3675 = 5,4423 cm eller
10,8844 cm diameter.
Omkretsen av en 2 cm sidovägg är P = 17 * 2 cm = 34 cm.
Exempel 2
Vad är området för en vanlig heptadecagon med en sida 2 cm?
Vi måste hänvisa till formeln som visas i föregående avsnitt, som gör det möjligt för oss att hitta en heptadeckons yta när den har längden d på din sida:
Heptadekagonarea = (17/4) (dtvå) / Solbränna (180º / 17)
Vid ersättning d = 2 cm i formeln ovan får du:
Område = 90,94 cm
Referenser
- C. E. A. (2003). Element av geometri: med övningar och kompassens geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Upptäck polygoner. Benchmark Education Company.
- Hendrik, V. (2013). Allmänna polygoner. Birkhäuser.
- IGER. (s.f.). Matematik första terminen Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren och Hornsby. (2006). Mathematics: Reasoning And Applications (tionde upplagan). Pearson Education.
- Patiño, M. (2006). Matematik 5. Redaktionellt program.
- Sada, M. 17-sidig regelbunden polygon med linjal och kompass. Återställd från: geogebra.org
- Wikipedia. Heptadecagon. Återställd från: es.wikipedia.com



Ingen har kommenterat den här artikeln än.