
Multiplikativ invers förklaring, exempel, lösta övningar
Det förstås av Invers multiplikativ av ett tal, ett annat tal som multipliceras med det första ger som ett resultat det neutrala elementet i produkten, det vill säga enheten. Om du har ett riktigt antal till därefter betecknas dess multiplikativa inversa med till-1, och det är sant att:
a a-1 = a-1 a = 1
Vanligtvis numret till tillhör en uppsättning reella tal.
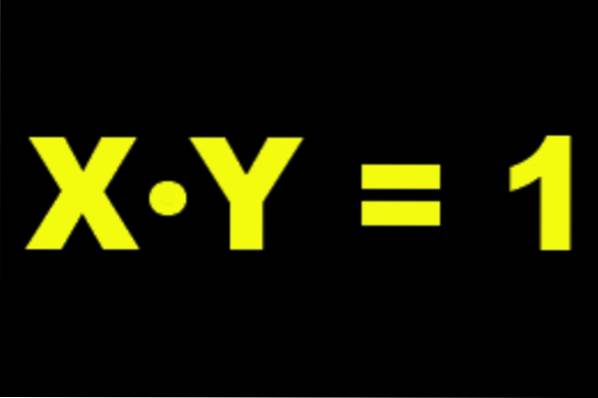
Om vi till exempel tar a = 2, då är dess multiplikator inversa två-1 = ½ eftersom följande är verifierat:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Till Invers multiplikativ av ett nummer kallas också ömsesidig, eftersom multiplikativ invers erhålls genom utbyte av täljare och nämnare, till exempel är multiplikativ invers av 3/4 4/3.
Som en allmän regel kan man säga att för ett rationellt tal (p / q) dess multiplikativa inversa (p / q)-1 Det är ömsesidigt (q / p) som kan verifieras nedan:
(p / q) ⋅ (p / q)-1 = (p / q) ⋅ (q / p) = (p⋅ q) / (q⋅ p) = (p⋅ q) / (p⋅ q) = 1
Den multiplikativa inversen finns inte i den numeriska uppsättningen heltal, Till exempel, om heltalet 2 tas, skulle dess multiplikativa invers enligt vad som har sett ovan vara ½, men a ½ är inte ett heltal..
Det finns inte heller någon multiplikativ invers av multipliceringselementet. Med andra ord har talet noll (0), som är nollelementet i multiplikationsoperationen, inte ett multiplikativt invers, eftersom det inte finns något tal som multipliceras med enheten noll.
Den multiplikativa inversen finns i rationella tal, i reella tal och i komplexa tal.
Exempel på multiplikativ invers
Exempel 1
Hitta multiplikativets invers av 3/2 och verifiera att den uppfyller egenskapen för multiplikativa heltal.
Enligt regeln ovan utbyts täljaren och nämnaren på detta sätt multiplikativ invers av (3/2) är (2/3). För att verifiera multipliceringen av de två siffrorna utförs:
(3/2) ⋅ (2/3) = (3 ⋅ 2) / (2 ⋅ 3) = 6/6 = 1.
För att multiplicera två bråknummer multiplicerar du helt enkelt täljaren för den första med täljaren för den andra för att få täljaren för resultatet..
För att erhålla nämnaren för en produkt med bråktal, fortsätt på ett liknande sätt, det vill säga multiplicera nämnarna med varandra och resultatet är nämnaren för produkten. I vårt exempel är det verifierat att täljaren av produkten för numret och dess ömsesidiga är 6 och nämnaren är 6, lämnar fraktionen 6/6 som är 1.
Exempel 2
Den multiplikativa inversen av -5 bör inte förväxlas med dess symmetriska (+5) som ibland kallas den aritmetiska inversen. Multiplikationsinversen kommer att erhållas enligt följande:
(-5) ⋅ X = 1
Där X är den multiplikativa invers som ska erhållas. En möjlig procedur är att lösa det okända X. Eftersom (-5) multiplicerar det okända X i den vänstra delen, så händer det att dela rätt medlem:
X = 1 / (-5)
Eftersom det är känt att + mellan - är -, så erhålls slutligen X:
X = - ⅕ .
Sammanfattningsvis - ⅕ är den multiplikativa inversen av -5.
Exempel 3
Skaffa multiplikativ invers av -√2. Antag att den multiplikativa inversen är X, då måste -√2 multipliceras med X vara enhet, ett villkor som vi ställer nedan:
-√2 ⋅ X = 1
Därefter delas båda medlemmarna med -√2 för att erhålla:
(-√2 ⋅ X) / (-√2) = 1 / (-√2)
I den första medlemmen är -√2 förenklad och lämnar:
X = 1 / (-√2)
Detta uttryck kan rationaliseras, det vill säga eliminera nämnarens rot, multiplicera i täljaren med (-√2) och i nämnaren med samma mängd så att resultatet inte ändras:
X = (-√2) / [(-√2) (- √2)] = - (√2 / 2)
Sammanfattningsvis - (√2 / 2) är den multiplikativa inversen av (-√2).
Exempel 4
Antag valfritt tal x, få dess multiplikativa invers och representera det grafiskt.
I detta fall är det en funktion f (x) = x, att erhålla multiplikativ invers är att hitta funktionen g (x) så att den multipliceras med enhetens första nummer. Funktionen g är den ömsesidiga f och bör inte på något sätt förväxlas med dess inversa funktion.
Med andra ord är den multiplikativa inversen av x en y så att följande är sant:
x ⋅ y = 1
från där clearing och du har:
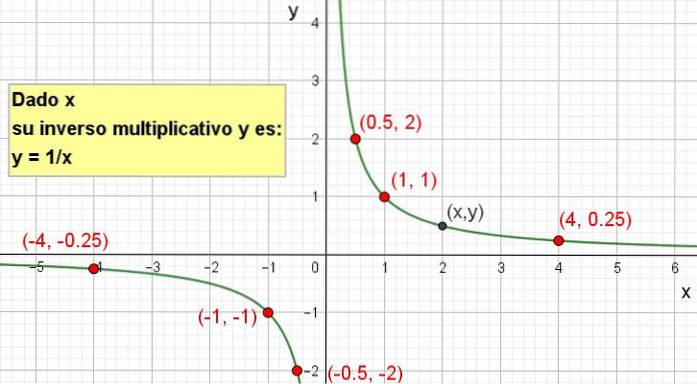
y = 1 / x.
Ovanstående tolkas sålunda med ett värde på x, den tidigare formeln ger oss dess multiplikativa inversa.
Det är möjligt att göra sin grafiska representation som visas i följande bild:
Träning
Övning 1
Med tanke på x = 2 - √2, få dess multiplikativa inversa y.
Lösning:
För att y ska vara en multiplikativ invers av x måste följande jämställdhet uppfyllas:
x ⋅ y = 1
Ersätt x med dess värde:
(2 - √2) ⋅ y = 1
Sedan rensas det och:
y = 1 / (2 - √2)
För att rationalisera resultatet multipliceras täljaren och nämnaren med sitt konjugerade binomium:
y = (2 + √2) / ((2 + √2) (2 - √2))
I nämnaren erkänns en anmärkningsvärd produkt som kallas produkten för en summa och en skillnad, vilket är skillnaden mellan rutorna. På detta sätt försvinner roten i nämnaren.
y = (2 + √2) / (2 ^ 2 - (√2) ^ 2)
Lösa krafterna:
y = (2 + √2) / (4 - 2)
Förenkla:
y = (2 + √2) / 2
Övning 2
Skaffa den multiplikativa inversen av (1 / a + 1 / b) där a och b inte är nollverkliga tal.
Lösning:
Vi kallar Y multiplikativ invers av (1 / a + 1 / b), så följande ekvation måste vara uppfylld:
Och ⋅ (1 / a + 1 / b) = 1
Variabeln Y rensas:
Y = 1 / (1 / a + 1 / b)
Nämnaren är löst:
Y = 1 / ((b + a) / a b)
Som känt från algebras regler övergår nämnaren till nämnaren:
Y = (a b) / (b + a)
Det beordras att äntligen få:
(a b) / (a + b) som är den multiplikativa inversen av (1 / a + 1 / b).
Övning 3
Skaffa multiplikationsinversen av (a - b) / (a ^ 2 - b ^ 2).
Lösning:
Kom ihåg att den multiplikativa inversen också kallas ömsesidigt eftersom den erhålls exakt genom att utbyta täljare och nämnare.
Då kommer den multiplikativa inversen av (a - b) / (a ^ 2 - b ^ 2) att vara:
(a ^ 2 - b ^ 2) / (a - b)
Men detta uttryck kan förenklas om vi, enligt reglerna för algebra, erkänner att täljaren är en skillnad i kvadrater som kan beräknas som produkten av en summa med en skillnad:
((a + b) (a - b)) / (a - b)
Eftersom det finns en gemensam faktor (a - b) i täljaren och nämnaren fortsätter vi med att förenkla och slutligen får:
(a + b) som är den multiplicerande inversen av (a - b) / (a ^ 2 - b ^ 2).
Referenser
- Fuentes, A. (2016). BASISK MATH En introduktion till kalkyl. Lulu.com.
- Garo, M. (2014). Matematik: kvadratiska ekvationer: Hur löser man en kvadratisk ekvation. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matematik för ledning och ekonomi. Pearson Education.
- Jiménez, J., Rofríguez, M., & Estrada, R. (2005). Matematik 1 SEP. Tröskel.
- Preciado, C. T. (2005). Matematikkurs 3: e. Redaktionellt Progreso.
- Rock, N. M. (2006). Algebra I Is Easy! Så enkelt. Team Rock Press.
- Sullivan, J. (2006). Algebra och trigonometri. Pearson Education.



Ingen har kommenterat den här artikeln än.