De Coulomb-lag det är den fysiska lagen som styr samspelet mellan elektriskt laddade föremål. Det förklarades av den franska forskaren Charles Augustin de Coulomb (1736-1806), tack vare resultaten från hans experiment med torsionsbalansen.
År 1785 experimenterade Coulomb otaliga gånger med små elektriskt laddade sfärer, till exempel att flytta två sfärer närmare eller längre ifrån varandra, varierande storleken på deras laddning och även deras tecken. Observera och registrera alltid varje svar noga.
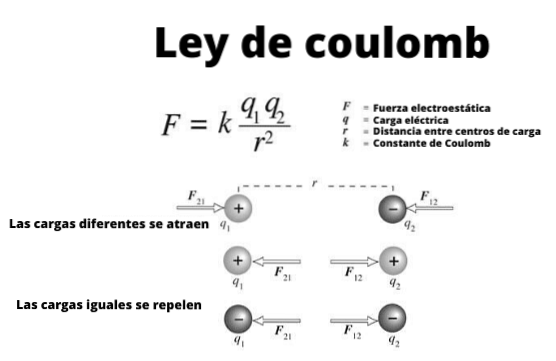
Dessa små sfärer kan betraktas som punktbelastningar, det vill säga föremål vars dimensioner är obetydliga. Och de uppfyller, som har varit känt sedan de antika grekernas tid, att laddningar av samma tecken stöter bort och de av ett annat tecken lockar..
Med detta i åtanke fann Charles Coulomb följande:
-Den attraktiva eller avstötande kraften mellan tvåpunktsladdningar är direkt proportionell mot produkten av laddningens storlek.
-Denna kraft riktas alltid längs linjen som går med i avgifterna.
-Slutligen är kraftens storlek omvänt proportionell mot kvadratet på avståndet mellan laddningarna.
Artikelindex
Tack vare dessa observationer drog Coulomb slutsatsen att kraftens storlek F mellan tvåpunktsavgifter Vad1 Y Vadtvå, separerade ett avstånd r, ges matematiskt som:
Eftersom kraften är en vektorstorlek definieras en enhetsvektor för att uttrycka den helt r i riktning mot linjen som förenar laddningarna (en enhetsvektor har en storlek lika med 1).
Dessutom kallas den proportionalitetskonstant som krävs för att omvandla det tidigare uttrycket till en jämlikhet koch eller helt enkelt k: den elektrostatisk konstant eller Coulomb är konstant.
Slutligen fastställs Coulombs lag för poängavgifter, som ges av:
Kraft, som alltid i det internationella systemet för enheter, kommer i newton (N). När det gäller avgifterna heter enheten coulomb (C) för att hedra Charles Coulomb och slutligen kommer avståndet r i meter (m).
När man tittar noga på ovanstående ekvation är det uppenbart att den elektrostatiska konstanten måste ha enheter N.mtvå / Ctvå, för att få newton som ett resultat. Värdet på konstanten bestämdes experimentellt som:
koch = 8,89 x 10 9 N.mtvå / Ctvå ≈ 9 x 10 9 N.mtvå / Ctvå
Figur 1 illustrerar samspelet mellan två elektriska laddningar: när de har samma tecken avvisar de, annars lockar de.
Observera att Coulombs lag överensstämmer med Newtons tredje lag eller handling och reaktion, därför är storleken på F1 Y Ftvå de är desamma, riktningen är densamma, men sinnena är motsatta.
För att lösa problem med interaktioner mellan elektriska laddningar måste följande beaktas:
- Ekvationen gäller uteslutande för punktladdningar, det vill säga elektriskt laddade föremål men med mycket små dimensioner. Om de laddade objekten har mätbara dimensioner är det nödvändigt att dela upp dem i mycket små belastningar och sedan lägga till bidrag för var och en av dessa laster, för vilka en integrerad beräkning krävs..
- Den elektriska kraften är en vektormängd. Om det finns mer än två samverkande laddningar, nettokraften på laddningen qi ges av superpositionsprincipen:
Fnetto = Fi1 + Fi2 + Fi3 + Fi4 +… = ∑ FI j
Där prenumerationen j är lika med 1, 2, 3, 4 ... och representerar var och en av de återstående laddningarna.
- Du bör alltid vara konsekvent med enheterna. Det vanligaste är att arbeta med den elektrostatiska konstanten i SI-enheter, då är det nödvändigt att se till att laddningarna är i coulomb och avstånden i meter.
- Slutligen gäller ekvationen när laddningarna är i statisk jämvikt.
I följande bild finns två punktsladdningar + q och + 2q. En tredje punkt laddning -q placeras vid P. Det ombeds att hitta den elektriska kraften på denna laddning på grund av närvaron av de andra.
Det första är att skapa ett lämpligt referenssystem, som i detta fall är den horisontella axeln eller x-axeln. Ursprunget till ett sådant system kan vara var som helst, men för enkelhets skull placeras det vid P, som visas i figur 4a:
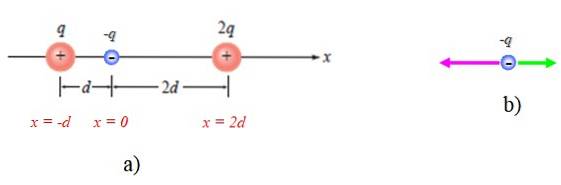
Ett diagram över krafterna på -q visas också med beaktande av att det lockas av de andra två (figur 4b).
Låt oss ringa F1 kraften som utövas av laddning q på laddning -q, riktas längs x-axeln och pekar i negativ riktning, därför:
Analogt beräknas det Ftvå:
Observera att storleken på Ftvå är hälften av det F1, även om lasten är dubbel. För att hitta nettokraften läggs de äntligen till i vektor F1 Y Ftvå:
Fnetto = (-k + k / 2). (qtvå / dtvå) (x) N = - (k / 2). (Qtvå / dtvå) (x) N
Två polystyrenkulor med lika massa m = 9,0 x 10-8 kg har samma positiva laddning Q och hängs upp av en sidentråd med längden L = 0,98 m. Sfärerna är åtskilda med ett avstånd på d = 2 cm. Beräkna värdet på Q.
Uttalningssituationen beskrivs i figur 5a.
Vi väljer en av sfärerna och på den ritar vi det isolerade kroppsdiagrammet, som innehåller tre krafter: vikt W, spänning i repet T och elektrostatisk avstötning F, som det visas i figur 5b. Och nu stegen:
Värdet på θ / 2 beräknas med triangeln i figur 5c:
θ / 2 = båge (1 x 10-två/0,98) = 0,585º
Därefter måste vi tillämpa Newtons andra lag och sätta den lika med 0, eftersom laddningarna är i statisk jämvikt. Viktigare är spänningen T är lutande och har två komponenter:
∑Fx = -T.sin θ + F = 0
∑FY = T.cos θ - W = 0
Vi löser storleken på spänningen från den sista ekvationen:
T = W / cos θ = mg / cos θ
Detta värde ersätts med den första ekvationen för att hitta storleken på F:
F = T sin θ = mg (sin θ / cos θ) = mg. tg θ
Eftersom F = k Qtvå / dtvå, rensar F:
Q = 2 × 10-elva C.
Det är enkelt att kontrollera Coulombs lag genom att använda en vridningsbalans som liknar den Coulomb använde i sitt laboratorium..
Det finns två små fläderbärsfärer, varav den ena, i mitten av balansen, är upphängd av en tråd. Experimentet består av att vidröra de utsläppta fläderbärsfärerna med en annan metallisk sfär laddad med Q-laddning.
Omedelbart fördelas laddningen lika mellan de två fläderbärsfärerna, men sedan, eftersom de är laddningar av samma tecken, stöter de från varandra. En kraft verkar på den upphängda sfären som orsakar vridning av tråden från vilken den hänger och omedelbart rör sig bort från den fasta sfären.
Sedan ser vi att det svänger några gånger tills det når jämvikt. Då balanseras vridningen på stången eller tråden som håller den av den elektrostatiska avstötningskraften.
Om sfärerna ursprungligen var vid 0 °, kommer den rörliga sfären nu att ha roterat en vinkel θ. Runt skalan finns ett tejp graderat i grader för att mäta denna vinkel. Genom att tidigare bestämma torsionskonstanten beräknas lätt den avstötande kraften och värdet på laddningen som erhållits av fläderbärsfärerna.
Ingen har kommenterat den här artikeln än.