
Ortogonala matrisegenskaper, bevis, exempel

Den har en ortogonal matris när nämnda matris multiplicerat med dess transponera resulterar i identitetsmatrisen. Om det inversa av en matris är lika med transponeringen är den ursprungliga matrisen ortogonal.
Rätvinkliga matriser har den egenskapen att antalet rader är lika med antalet kolumner. Radvektorerna är också ortogonala enhetsvektorer och de transponerande radvektorerna är också.
När en ortogonal matris multipliceras med vektorerna i ett vektorutrymme producerar den en isometrisk transformation, det vill säga en transformation som inte förändrar avstånden och bevarar vinklarna.
En typisk representant för ortogonala matriser är rotationsmatriser. Transformationerna av ortogonala matriser på ett vektorutrymme kallas ortogonala transformationer.
De geometriska transformationerna av rotation och reflektion av punkter som representeras av deras kartesiska vektorer utförs genom att applicera ortogonala matriser på originalvektorerna för att erhålla koordinaterna för de transformerade vektorerna. Det är av denna anledning som ortogonala matriser används i stor utsträckning vid beräkningsgrafikbehandling..
Artikelindex
- 1 Fastigheter
- 2 Demo
- 3 Exempel
- 3.1 Exempel 1
- 3.2 Exempel 2
- 3.3 Exempel 3
- 3.4 Exempel 4
- 4 Referenser
Egenskaper
En matris M är ortogonalt om det multipliceras med dess transponering MT returnerar identitetsmatrisen Jag. På samma sätt resulterar produkten i transponeringen av en ortogonal matris med den ursprungliga matrisen i identitetsmatrisen:
M MT = MT M = jag
Som en konsekvens av föregående uttalande har vi att transponera en ortogonal matris är lika med dess inversa matris:
MT = M-1.
Uppsättningen av ortogonala matriser n x n bildar gruppen ortogonal O (n). Och delmängden av O (n) av ortogonala matriser med determinant +1 bildar Grupp av enhetliga specialmatriser SU (n). Gruppmatriserna Sol) är matriser som producerar linjära rotationstransformationer, även kända som rotationsgrupp.
Demonstration
Låt oss visa att en matris är ortogonal om, och endast om radvektorerna (eller kolumnvektorerna) är ortogonala mot varandra och av norm 1.
Antag att raderna i en ortogonal matris n x n är n ortonormala vektorer med dimensionen n. Om det betecknas med v1, vtvå,…., Vn n-vektorerna är nöjda:
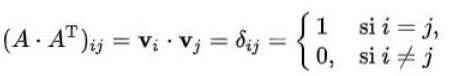
Där det är uppenbart att uppsättningen radvektorer verkligen är en uppsättning ortogonala vektorer med normala.
Exempel
Exempel 1
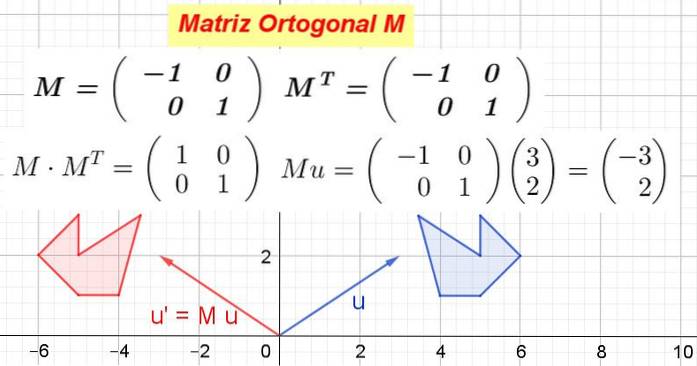
Visa att 2 x 2-matrisen som i sin första rad har vektorn v1= (-1 0) och i sin andra rad vektorn v2= (0 1) är en ortogonal matris.
Lösning: Matrisen är byggd M och dess införlivande beräknas MT:
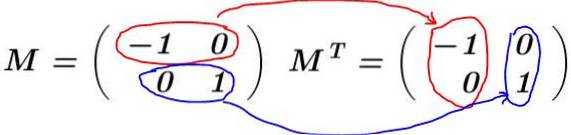
I det här exemplet är arrayen M den är självtransponerad, det vill säga matrisen och dess transponering är identiska. Det multipliceras M genom dess införlivande MT:
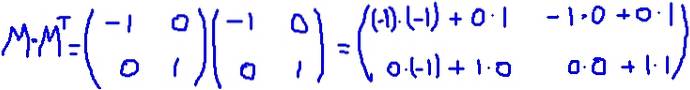
Det är verifierat att M MT är lika med identitetsmatrisen:
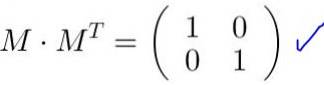
När matrisen M multipliceras med koordinaterna för en vektor eller en punkt, erhålls nya koordinater som motsvarar transformationen som matrisen gör på vektorn eller punkten.
Figur 1 visar hur M transformera vektor eller på eller' och även hur M förvandla den blå polygonen till den röda polygonen. Vad M är ortogonal är det då en ortogonal transformation som bevarar avstånden och vinklarna.
Exempel 2
Antag att du har en 2 x 2 matris definierad i realerna som ges av följande uttryck:
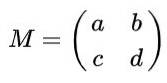
Hitta de verkliga värdena för till, b, c Y d så att matrisen M vara en ortogonal matris.
Lösning: Per definition är en matris ortogonal om den multipliceras med dess transponering erhålls identitetsmatrisen. Kom ihåg att den transponerade matrisen erhålls från originalet, utbyter rader mot kolumner, följande jämställdhet erhålls:
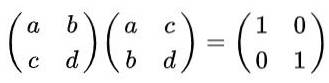
Genomföra den matrismultiplikation vi har:
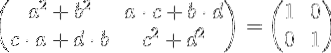
Utjämning av elementen i den vänstra matrisen med elementen i identitetsmatrisen till höger, vi får ett system med fyra ekvationer med fyra okända a, b, c och d.
Vi föreslår följande uttryck för a, b, c och d i termer av trigonometriska förhållanden sinus och cosinus:
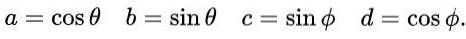
Med detta förslag och på grund av den grundläggande trigonometriska identiteten uppfylls de första och tredje ekvationerna automatiskt i likvärdigheten av matriselementen. Den tredje och fjärde ekvationen är desamma och i matrisjämlikhet efter att ha ersatt de föreslagna värdena ser det ut så här:
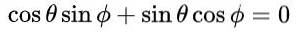
vilket leder till följande lösning:
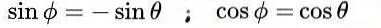
Slutligen erhålls följande lösningar för den ortogonala matrisen M:
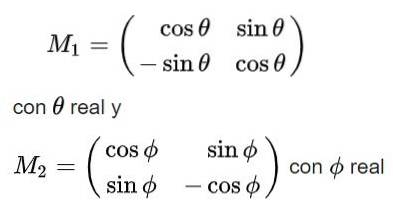
Observera att den första lösningen har determinant +1 så att den tillhör gruppen SU (2), medan den andra lösningen har determinant -1 och därför inte tillhör denna grupp.
Exempel 3
Med tanke på följande matris, hitta värdena a och b så att vi har en ortogonal matris.
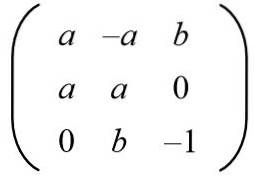
Lösning: För att en given matris ska vara ortogonal måste produkten med dess transponering vara identitetsmatrisen. Därefter utförs matrisprodukten för den givna matrisen med dess transponerade matris, vilket ger följande resultat:
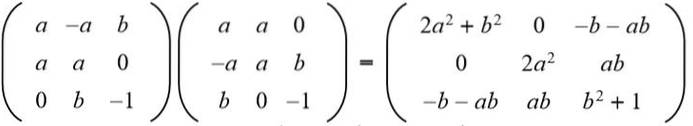
Därefter likställs resultatet med 3 x 3 identitetsmatrisen:
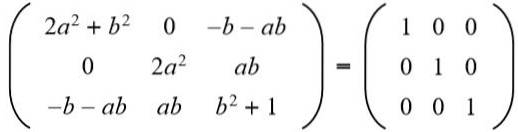
I den andra raden tredje kolumnen har vi (a b = 0), men till det kan inte vara noll, för om så är fallet, skulle inte likheten mellan elementen i andra raden och andra kolumnen uppfyllas. Då nödvändigtvis b = 0. Ersätter b för värdet 0 har vi:
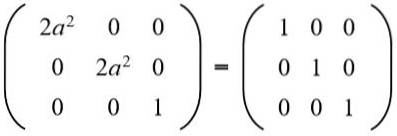
Sedan löses ekvationen: 2a ^ 2 = 1, vars lösningar är: + ½√2 och -½√2.
Tar den positiva lösningen för till följande ortogonala matris erhålls:
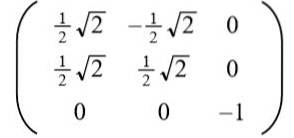
Läsaren kan enkelt verifiera att radvektorerna (och även kolumnvektorerna) är ortogonala och enhetliga, det vill säga ortonormala.
Exempel 4
Bevisa att matrisen TILL vars radvektorer är v1 = (0, -1 0), v2 = (1, 0, 0) Y v3 = (0 0 -1) är en ortogonal matris. Hitta också hur vektorerna i den kanoniska basen transformeras Jag J K till vektorer u1, u2 Y u3.
Lösning: Man bör komma ihåg att elementet (i, j) i en matris multiplicerat med dess transponering, är punktprodukten för vektorn i rad (i) med den i kolumnen (j) i transponeringen. Dessutom är denna produkt lika med Kronecker-deltaet om matrisen är ortogonal:
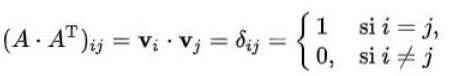
I vårt fall ser det ut så här:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
Med vilken det visas att det är en ortogonal matris.
Vad mer u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) och slutligen u3 = A k = (0, 0, -1)
Referenser
- Anthony Nicolaides (1994) Determinants & Matrices. Godkänn publikation.
- Birkhoff och MacLane. (1980). Modern algebra, red. Vicens-Vives, Madrid.
- Casteleiro Villalba M. (2004) Introduktion till linjär algebra. ESIC Ledare.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Students Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics. Ivy press begränsad.
- Wikipedia. Rätvinklig matris. Återställd från: es.wikipedia.com
- Wikipedia. Rätvinklig matris. Återställd från: en.wikipedia.com



Ingen har kommenterat den här artikeln än.