
Uniform cirkulär rörelse (M.C.U.) formler, egenskaper

En partikel har cirkulär rörelse enhetlig (M.C.U.) när dess bana är en omkrets och den också färdas med konstant hastighet. Många föremål som delar av maskiner och motorer har till exempel denna typ av rörelse, bland annat datorhårddiskar, fläktblad, axlar och många andra saker som sticker ut..
Enhetlig cirkulär rörelse är också en bra approximation för rörelsen hos vissa himmellegemer såsom jorden. Egentligen är jordens bana elliptisk, vilket framgår av Keplers lagar. Banans excentricitet är dock liten och som en första approximation kan den betraktas som cirkulär, vilket förenklar vissa beräkningar, som att hitta jordens hastighet när den rör sig runt solen..
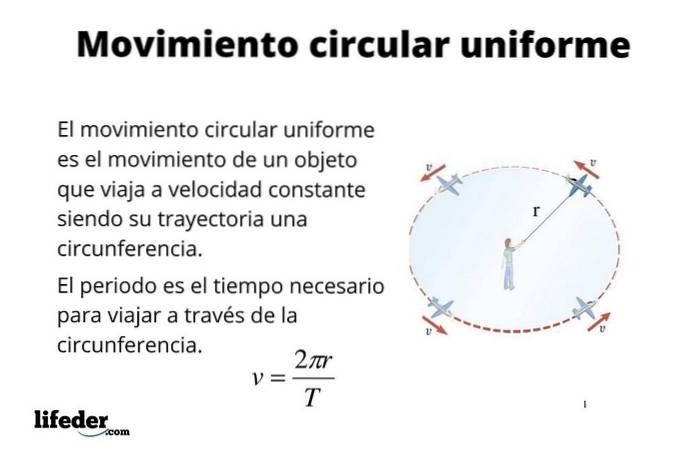
Vid beskrivning av enhetlig cirkelrörelse används samma parametrar som vid rätlinjig rörelse, nämligen: position, förskjutning, tid, hastighet och acceleration..
Acceleration? Ja, i själva verket accelereras enhetlig cirkelrörelse även om dess hastighet v vara konstant. Detta beror på att hastigheten v, vilket är en vektor och det är därför den är fet, och ändrar kontinuerligt sin riktning när objektet eller partikeln roterar. Varje förändring i v produceras av en acceleration, som, såsom kommer att ses, är riktad mot centrum av den cirkulära banan.
Enhetlig cirkelrörelse är rörelse i planet xy, därför är det en rörelse i två dimensioner. Det är emellertid möjligt att uttrycka det bekvämare med hjälp av den vinkel θ som partikeln sveper, mätt i förhållande till den horisontella axeln eller en annan lämplig referensaxel..
Även om det är ett förlängt objekt sveper dess partiklar alltid samma vinkel, även om de har olika koordinater. (x, y).
Artikelindex
- 1 Egenskaper för enhetlig cirkelrörelse
- 2 Formler för enhetlig cirkelrörelse
- 2.1 Positionsvektor
- 2.2 Vinkelhastighet och linjär hastighet
- 2.3 Centripetal acceleration
- 2.4 Period och frekvens
- 3 Exempel på enhetlig cirkelrörelse
- 3.1 Jordens rörelse
- 3.2 Partiklar på kanten av en skiva
- 3.3 Hubble-rymdteleskop
- 3.4 Centrifuger
- 3.5 Trädgårdssprinkler
- 3.6 Sport
- 4 Övningen löst
- 5 Referenser
Egenskaper för enhetlig cirkelrörelse
Egenskaperna för enhetlig cirkelrörelse kan sammanfattas enligt följande:
-Banan är en omkrets, därför är den en rörelse i planet.
-Farten v är konstant, men hastigheten v nej, eftersom det ständigt ändrar riktning och riktning för att tillgodose mobilens tur.
-Hastighetsvektorn v är alltid tangentiellt för omkretsen och vinkelrätt mot radiell riktning.
-Vinkelhastigheten ω är konstant.
-Trots att det är enhetligt finns det en acceleration för att förklara dessa förändringar i hastighetsriktningen. Denna acceleration är centripetalacceleration.
-Centripetalacceleration och hastighet är vinkelräta mot varandra.
-Det är en periodisk eller repetitiv rörelse, därför definieras period och frekvensstorlekar för den.
Likformiga formler för cirkulär rörelse
I detta schema finns en partikel P som snurrar moturs med MCU, enligt riktningen och känslan av hastighetsvektorn v dras.
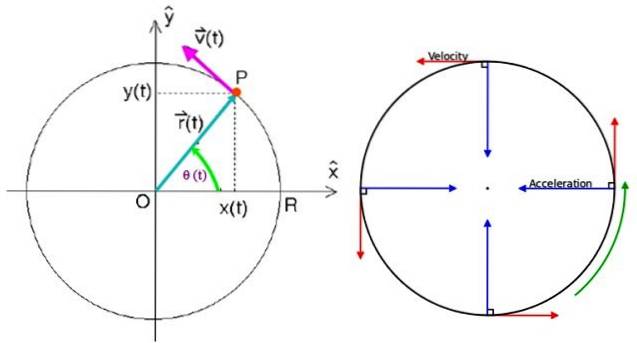
För att specificera positionsvektorn är det nödvändigt att ha en referenspunkt och idealpunkten är centrum för omkretsen O som sammanfaller med centrum för det kartesiska koordinatsystemet i xy-planet.
Positionsvektor
Det betecknas som r (t) och riktas från ursprunget till den punkt P där partikeln är belägen. Vid ett givet ögonblick skrivs det i kartesiska koordinater som:
r (t) = x (t) i + och t) j
Var i Y j är enhetsvektorerna vinkelräta i riktningarna x och Y respektive. Från diagrammet kan man se att vektormodulen r (t) alltid värt R, omkretsens radie. Om θ är bildad vinkel r med den horisontella axeln är positionen också lika med:
r (t) = [Rcos θ(t)] i +[Rsen θ(t)] j
Vinkeln den bildar r (t) med den horisontella axeln är en central vinkel och dess värde är:
θ = s / R
Var s är omkretsens båge och R-radien. Nämnda vinkel θ är en funktion av tiden, så den kan skrivas θ = θ (t), ring upp vinkelposition.
Eftersom hastigheten är konstant, beskriver partikeln lika vinklar i lika tider och i analogi med den enhetliga rätlinjiga rörelsen skrivs det:
θ = θ (t) = θeller + .t
Här θeller är den initiala vinkeln mätt i radianer i förhållande till referensaxeln, den kan vara 0 eller vilket värde som helst och ω är vinkelhastigheten.
Vinkelhastighet och linjär hastighet
Vinkelhastighet är det första derivatet av vinkelposition och betecknas som ω. Dess värde är konstant för likformig cirkelrörelse, eftersom lika vinklar svepas på samma tid. Med andra ord:

Enheterna med linjär hastighet i enhetlig cirkelrörelse är desamma som för linjär rörelse: m / s (i SI International System), km / h, cm / s och andra..
Centripetal acceleration
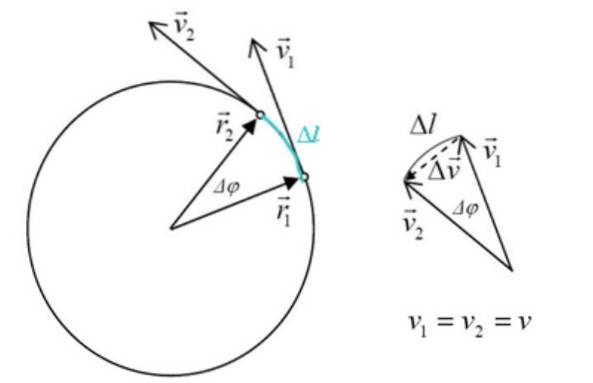
I figuren nedan finns en partikel som rör sig medurs runt omkretsen med konstant hastighet. Detta innebär att hastighetsvektorn alltid har samma modul men ändrar riktning för att passa omkretsen.

Varje hastighetsförändring resulterar i acceleration, som per definition är:

Triangeln bildad av vtvå, v1 och Δv liknar triangeln av sidor rtvå, r1 och Δl, där Δφ är den centrala vinkeln. Storleken på rtvå Y r1 de är desamma, så:
rtvå = r1 = r
Sedan, av båda trianglarna har vi dessa relationer för vinkeln:
Aj = Ar / r; Aφ = Av / v
Den djärva typen är inte nödvändig, eftersom måttet på vinkeln beror på storleken på dessa vektorer. Matchande av de föregående uttrycken följer att:





Period och frekvens
Eftersom den cirkulära rörelsen är repetitiv definieras perioden T samma tid som det tar för mobilen att göra en hel sväng. Eftersom längden på radien R är 2πR, är vinkeln som sveps i radianer vid full varv 2π radianer och det tar tid T, vinkelhastigheten är:
ω = 2π / T
T = 2π / ω
Perioden med enhetlig cirkelrörelse mäts i sekunder i det internationella systemet.
För sin del, frekvensen F är antalet varv per tidsenhet och är periodens ömsesidiga eller inversa:
f = n / t = 1 / T.
Frekvensenheten i det internationella systemet är s-1.
Exempel på enhetlig cirkelrörelse
Många föremål roterar för att producera olika effekter: hjul, skivor och turbiner. När arbetshastigheten har uppnåtts utförs vanligtvis rotation med konstant hastighet. Cirkelrörelse är så vanligt i vardagen att du knappast tänker på det, så här är några nära exempel som illustrerar det mycket bra:
Jordens rörelse

Jorden och de andra planeterna i solsystemet rör sig i elliptiska banor med liten excentricitet, förutom kvicksilver, vilket innebär att i första approximationen kan man anta att deras rörelse är enhetlig cirkulär.
Med detta har du en bra uppfattning om hastigheten på översättningen runt solen, eftersom det rör sig om jorden är rörelseperioden känd: ett år eller 365 dagar..
Partiklar på kanten av en skiva

Partiklarna som roterar på kanten av en gammal skivspelare eller bladet på en fläkt, följer en jämn cirkelrörelse när enheten når uppspelningshastigheten.
Hubble-rymdteleskop

Hubble-rymdteleskopet kretsar runt jorden vid cirka 7550 m / s.
Centrifuger
Tvättmaskinerna utför en snurrprocess för att klämma kläderna, som består av att rotera behållartrumman i hög hastighet. Torkarna roterar också under en tidsperiod i en jämn cirkelrörelse..
Centrifugering används också i laboratorier för att exempelvis separera föreningar och därmed separera deras beståndsdelar genom skillnad i densiteter. Närhelst vi pratar om centrifugering finns det en cirkelrörelse som är enhetlig, åtminstone en tid.
Trädgårdsvattenburkar
Många trädgårdssprinklers roterar med konstant hastighet så att marken vattnas jämnt..
sporter

I hammarkastet till exempel, som är en olympisk disciplin, snurrar idrottaren en metallboll med kraft med hjälp av en stålkabel fäst vid greppet. Målet är att skicka bollen så långt som möjligt, men utan att lämna ett visst område.
Övningen löst
En partikel rör sig i en omkrets av radien 2m med konstant hastighet v = 8 m / s, moturs. Ursprungligen var partikeln i r = +2 j m. Beräkna:
a) Vinkelhastigheten ω
b) Dess vinkelposition θ (t)
c) Rörelseperioden
d) Centripetal acceleration.
e) Partikelns position efter att ha passerat t = π / 4 s
Lösning till
Från formeln v = Rω följer att:
ω = v / R = (8 m / s) / 2m = 4rad ∙ s-1
Lösning b
Med den positiva x-axeln som referensaxel är partikeln initialt 90 ° = π / 2 radianer i förhållande till axeln, eftersom uttalandet säger att startpositionen är +2 j m, det vill säga partikeln är på y = 2m när rörelsen börjar följa.
θ = θ (t) = θeller + ωt = π / 2 + 4t
Lösning c
T = 2π / ω = 2π / 4 s = 0,5 π s
Lösning d
a = vtvå / R = (8 m / s)två / 2 m = 32 m / stvå
Lösning e
θ (t) = π / 2 + 4t → θ (π / 4) = π / 2 + 4 ∙ (π / 4) = 3π / 2 radianer
Detta betyder att partikeln efter den tiden är i positionen y = -2m j. Det är vettigt eftersom t = π / 4 s är halva perioden, därför reste partikeln en 180 ° vinkel moturs från dess ursprungsläge och den måste vara precis i motsatt position.
Referenser
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.
- Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Red. Volym 1. Pearson.
- Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7: e. Ed. Cengage Learning.
- Zapata, F. Cirkulär rörelse. Återställd från: francesphysics.blogspot.com.



Ingen har kommenterat den här artikeln än.