
Elliptisk rörelse
Vad är elliptisk rörelse?
I elliptisk rörelse beskriver mobilen en ellips, precis som planeterna gör runt solen, och månen och konstgjorda satelliter runt jorden, för att nämna några bekanta exempel..
Kraften som ger upphov till denna rörelse är tyngdkraften, en central kraft. Dessa typer av krafter riktas mot (eller från) en fast punkt O, och deras modul beror på avståndet till den punkten. Om r är avståndet och ellerr är enhetsvektorn i radiell riktning, den centrala kraften F är en vektorfunktion av formen:
F = F (r) ellerr
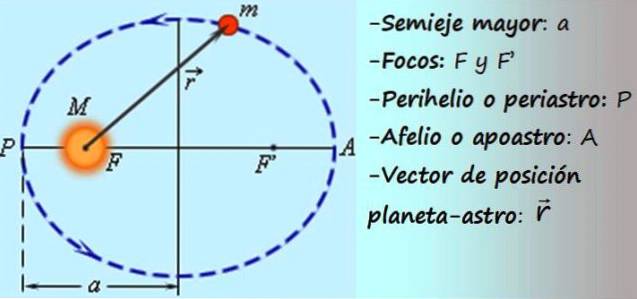
Med en del matematik kan det visas att rörelsen av ett objekt under tyngdkraftsverkan följer en av dessa fyra banor: ellips, omkrets, hyperbol eller parabel.
Egenskaper för den elliptiska rörelsen
Några av de viktigaste egenskaperna för elliptisk rörelse under central kraft är:
-Vinkelmomentet med avseende på O bevaras, kallas L och som beräknas genom vektorprodukten mellan positions- och hastighetsvektorerna: L = r × mv, där m representerar massan av det rörliga objektet.
-Den elliptiska banan ligger i planet bestämt av vektorerna r Y v.
-Från bevarande av vinkelmoment så kallade lagar av områden, vilket fastställer att mobilen färdas lika stora områden på lika tid.
-Mekanisk energi bevaras också i elliptisk rörelse om det inte finns några dissipativa krafter.
-Tiden det tar för mobilen att ge en bana och dess totala energi beror bara på längden "a" på ellipsens halvhuvudaxel..
Skillnader med cirkulär rörelse
Även om objektet rör sig både i cirkulär och elliptisk rörelse i en sluten och repetitiv väg, det vill säga periodisk, finns det uppenbara skillnader mellan en rörelse och en annan, såsom:
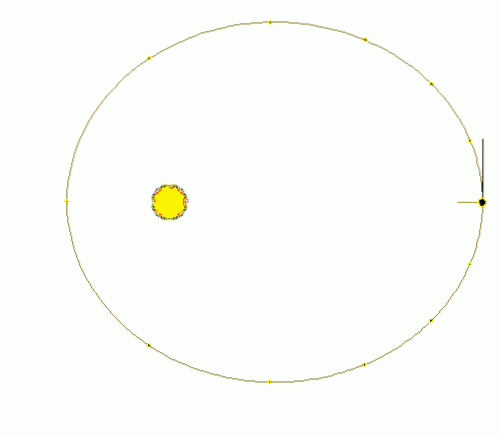
-I cirkulär rörelse beskriver mobilen en omkrets vars radie (avstånd till banans centrum) är konstant, medan den i elliptisk rörelse beskriver en ellips, där avståndet till banans centrum är variabelt (se figur 1).
-I fallet med likformig cirkulär rörelse MCU sveper mobilen lika vinklar på lika tid, men i planetell elliptisk rörelse sveps lika områden i lika stora tider. Detta är lagen om områden, även känd som Keplers andra lag om planetrörelse..
Viktiga ekvationer av planetell elliptisk rörelse
Period
I elliptisk rörelse härrörande från gravitationell attraktion är rörelseperioden den tid det tar för planeten eller satelliten (m) att göra en elliptisk sväng runt solen eller jorden (M). När energibesparingen tillämpas följer det att den är proportionell mot kuben på längden på ellipsens halvhuvudaxel:

Där G är den universella gravitationskonstanten: 6,67 × 10-elva N ∙ mtvå/ kgtvå, M är solens, jordens eller föremålets massa som orsakar växelverkan på m och "a" är längden på halvhuvudaxeln.
Mekanisk energi
Den totala energin för planeten (m) - Sun (M) -systemet är:

Vinkelmoment
Storleken på vinkelmomentet vid en punkt på den elliptiska banan beror också på längden på den halvhuvudaxeln, liksom på excentriciteten "e", en måttlös parameter som indikerar hur platt ellipsen är. Om e = 0 blir ellipsen en cirkel.

Hastighet
Hastighetens storlek ges av följande ekvation:

Där r är avståndet mellan en punkt på omloppsbana (planetens plats) och fokus (sol).
Exempel på elliptisk rörelse
Planetrörelser
Keplers första lag säger att planeternas rörelse runt solen följer en elliptisk väg, med solen i en av fokuserna. Vissa kometer som regelbundet besöker jorden, som Halleys komet, följer också en elliptisk rörelse..
Bortsett från denna elliptiska translationella rörelse och den som roterar runt deras axel, har planeterna sina egna rörelser på grund av de komplexa gravitationsinteraktionerna med de andra planeterna och himmellegemerna i solsystemet. På detta sätt är de precession och nutationsrörelser som jorden besitter och som beror på den gemensamma gravitationella attraktionen mellan solen och månen..
I precession beskriver jordens axel en kon när den roterar runt axeln vinkelrätt mot planen eller ekliptiken. Och i nutation, som läggs ovanpå precessionen, svänger jordens axel upp och ner i en elliptisk slinga var 18,6 år. Totalt 1385 av dessa slingor sedan på 25 767 år, vilket är perioden för jordens axel.
En partikel med havsvatten
I havsvatten utför en partikel en elliptisk rörelse, där ellipsen blir mer och mer platt med ökande djup. Å andra sidan, när vattnet är djupt, är partiklarnas rörelse cirkulär.
Vad som händer är att när vågen närmar sig kusten uppstår friktionskrafter tack vare dess närhet till botten, och denna friktion tenderar att sakta ner rörelsen i nedre delen av banan, medan toppen fortsätter sin rörelse..
Resultatet är att omkretsen blir plattare och effekten accentueras när djupet ökar..

Elliptiskt svängningssätt i en fysisk pendel
En fysisk pendel består av ett styvt fast ämne som kan svänga i ett plan runt en axel vinkelrät mot den. Om objektet får röra sig fritt kan det beskriva vilken vinkel som helst runt axeln som förenar masscentrum med upphängningspunkten, samt kan rotera runt den..
Tack vare jordens rotation kan pendeln beskriva banor med ungefär elliptisk form, vilka är kända som elliptiska svängningssätt, kännetecknade av en annan vinkelmoment än 0.
Det finns också planläge (vinkelmoment 0) och koniskt läge (annat vinkelmoment än 0), det senare med en cirkulär bana i ett horisontellt plan.
Elliptiska cyklar
De elliptiska rörelserna som beskrivits tidigare förekommer i naturen, men kan också användas för att göra användbara prylar, såsom elliptiska cyklar, som är mycket populära maskiner för aerobics..
De är stillastående cyklar som i grunden består av ett styr och två pedaler som personen aktiverar genom att trycka på sig själv med sin vikt och beskriva en ellips med fötterna. Detta är en naturlig rörelse med låg effekt som är fördelaktig eftersom den rör sig många muskelgrupper i hela kroppen..
Referenser
- Astronomi för alla. Precession och nutation. Återställd från: astronomiaparatodos.com.
- Beräkning av hastigheten i elliptiska banor. Återställd från: forum.lawebdefisica.com.
- Fowler, Michael. Elliptiska banor: vägar till planeterna. Återställd från: galileo.phys.virginia.edu.
- Hernández, J. Studie av svängningslägena i en symmetrisk fysisk pendel med den effektiva potentialen. Återställd från: scielo.org.co.
- Kittel, C. 1973. Mekanik. Berkeley fysik kurs. Volym 1. Ed. Reverté.
- Elliptiska banor under inverkan av central kraft. Återställd från: sc.ehu.es.
- Konservativa system. Återställd från: dfmf.uned.es.Wikipedia. Elliptisk bana. Återställd från: en.wikipedia.org.



Ingen har kommenterat den här artikeln än.