Imaginära nummeregenskaper, applikationer, exempel

De imaginära siffror är de som ger en lösning på ekvationen där det okända, kvadratiska, är lika med ett negativt reellt tal. Den imaginära enheten är i = √ (-1).

I ekvationen: z^två= - a, z är ett imaginärt tal som uttrycks enligt följande:

 z = √ (-a) = i√ (a)

Varelse till ett positivt reellt tal. Ja a = 1, sedan z = i, var i är den imaginära enheten.

I allmänhet uttrycks alltid ett rent imaginärt tal z i formen: 

z = y⋅i

Var Y är ett verkligt tal e i är den imaginära enheten.

Precis som verkliga siffror representeras på en rad, kallad riktigt rak, på ett analogt sätt representeras de imaginära siffrorna på imaginär linje.

De imaginär linje är alltid ortogonalt (90 ° form) till riktigt rak och de två raderna definierar ett kartesiskt plan som kallas komplexa plan.

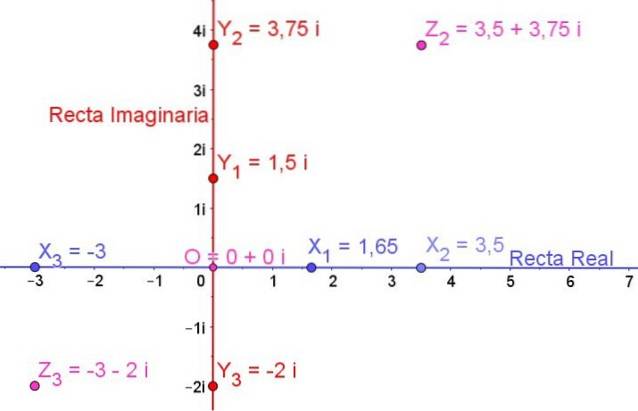
I figur 1 visas det komplexa planet och på det representeras några reella tal, några imaginära tal och även några komplexa tal:

X₁, X_två, X₃ de är verkliga siffror

Y₁, Y_två, Y₃ de är imaginära siffror

Z_två och Z₃ de är komplexa tal

Talet O är den verkliga nollan och det är också den imaginära nollan, så ursprunget O är den komplexa nollan uttryckt av:

0 + 0i 

Artikelindex

• 1 Fastigheter
  • 1.1 Addition och subtraktion av imaginära
  • 1.2 Produkt av fantasier
  • 1.3 Produkt av ett reellt tal av en annan imaginär
  • 1.4 Empowerment of an imaginary
  • 1.5 Summan av ett reellt tal och ett imaginärt tal
• 2 applikationer
• 3 Övningar med imaginära siffror
  • 3.1 - Övning 1
  • 3.2 - Övning 2
  • 3.3 - Övning 3
  • 3.4 - Övning 4
  • 3.5 - Övning 5
  • 3.6 - Övning 6
• 4 Referenser

Egenskaper

Uppsättningen av imaginära nummer betecknas med:

I = …, -3i,…, -2i,…., - i,…., 0i,…., I,…., 2i,…., 3i,…

Och du kan definiera vissa operationer på denna numeriska uppsättning. Ett imaginärt nummer erhålls inte alltid från dessa operationer, så låt oss titta lite mer på dem:

Addition och subtraktion av imaginära

Imaginära nummer kan läggas till och subtraheras från varandra, vilket resulterar i ett nytt imaginärt nummer. Till exempel:

 3i + 2i = 5i

4i - 7i = -3i

Produkt av imaginära

När produkten av ett imaginärt nummer med ett annat görs blir resultatet ett reellt tal. Låt oss göra följande för att kontrollera det:

2i x 3i = 6 x i^två = 6 x (√ (-1))^två = 6 x (-1) = -6.

Och som vi kan se är -6 ett verkligt tal, även om det har erhållits genom att multiplicera två rena imaginära tal.

Produkt av ett reellt tal av en annan imaginär

Om ett reellt tal multipliceras med i, blir resultatet ett imaginärt tal, vilket motsvarar en 90 graders rotation moturs.

Och det är som jag^två motsvarar två på varandra följande rotationer på 90 grader, vilket motsvarar att multiplicera med -1, det vill säga i^två = -1. Det kan ses i följande diagram:

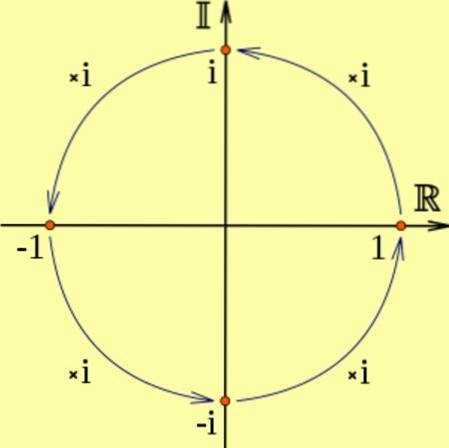
Till exempel:

-3 x 5i = -15i

-3 x i = -3i.

Empowerment av en imaginär

Du kan definiera potentiering av ett imaginärt tal till ett heltalsexponent:

i¹ = i

i^två = i x i = √ (-1) x √ (-1) = -1

i³ = i x i^två = -i

i⁴ = i^två x i^två = -1 x -1 = 1

i⁵ = i x i⁴ = i

I allmänhet måste du iⁿ = i ^ (n mod 4), var mod är resten av uppdelningen mellan n Y 4.

Negativ heltalspotentialisering kan också utföras:

i^-1 = 1 / i¹ = i / (i x i¹) = i / (i^två) = i / (-1) = -i

i-^två = 1 / i^två = 1 / (-1) = -1

i-³= 1 / i³ = 1 / (- i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

I allmänhet är det imaginära talet b⋅i som höjs till kraften n:

(b⋅i) iⁿ = bⁿ iⁿ = bⁿ i ^ (n mod 4)

Några exempel är följande:

(5 i)¹² = 5¹² i¹² = 5¹² i⁰ = 5¹² x 1 = 244140625

(5 i)^elva = 5^elva i^elva = 5^elva i³ = 5^elva x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ i¹⁰ = 2¹⁰ i^två = 1024 x (-1) = -1024

Summan av ett reellt tal och ett imaginärt tal

När du lägger till ett riktigt tal med ett imaginärt tal blir resultatet varken verkligt eller imaginärt, det är en ny typ av nummer som heter komplext tal.

Till exempel, om X = 3,5 och Y = 3,75i, är resultatet det komplexa talet:

Z = X + Y = 3,5 + 3,75 i

Observera att i summan kan de verkliga och imaginära delarna inte grupperas tillsammans, så ett komplext antal kommer alltid att ha en riktig del och en imaginär del..

Denna operation utökar uppsättningen reella tal till det största komplexa talet.

Applikationer

Namnet på imaginära siffror föreslogs av den franska matematikern René Descartes (1596-1650) som ett hån eller meningsskiljaktighet med förslaget av detsamma från den italienska matematikern Raffaelle Bombelli.

Andra stora matematiker, som Euler och Leibniz, stödde Descartes i denna oenighet och kallade imaginära siffror amfibie nummer, som slits mellan att vara och ingenting.

Namnet på imaginära siffror kvarstår idag, men deras existens och betydelse är mycket verklig och påtaglig, eftersom de förekommer naturligt inom många fysikområden som:

-Relativitetsteorin.

-I elektromagnetism.

-Kvantmekanik.

Övningar med imaginära siffror

- Övning 1

Hitta lösningarna i följande ekvation:

z^två + 16 = 0

Lösning

z^två = -16

Att ta kvadratrot i båda medlemmarna har vi:

√ (z^två ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Med andra ord är lösningarna i den ursprungliga ekvationen:

z = + 4i eller z = -4i.

- Övning 2

Hitta resultatet av att höja den imaginära enheten till effekten 5 minus subtraheringen av den imaginära enheten som höjs till effekten -5.

Lösning

i⁵ - i-⁵ = i⁵ - 1 / i⁵ = i - 1 / i = i - (i) / (i x i) = i - i / (- 1) = i + i = 2i

- Övning 3

Hitta resultatet av följande operation:

(3i)³ + 9i 

Lösning

3³ i³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Övning 4

Hitta lösningarna i följande kvadratiska ekvation:

(-2x)^två + 2 = 0

Lösning

Ekvationen ordnas på följande sätt:

(-2x)^två = -2

Sedan tas kvadratroten av båda medlemmarna

√ ((- 2x)^två) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Sedan löser vi för x för att äntligen få:

x = ± √2 / 2 i

Det vill säga det finns två möjliga lösningar:

x = (√2 / 2) i

Eller den här andra:

x = - (√2 / 2) i

- Övning 5

Hitta värdet på Z definierat av:

Z = √ (-9) √ (-4) + 7

Lösning

Vi vet att kvadratroten av ett negativt reellt tal är ett imaginärt tal, till exempel √ (-9) är lika med √ (9) x √ (-1) = 3i.

Å andra sidan är √ (-4) lika med √ (4) x √ (-1) = 2i.

Så den ursprungliga ekvationen kan ersättas med:

3i x 2i - 7 = 6 i^två - 7 = 6 (-1) - 7 = -6 - 7 = -13

- Övning 6

Hitta värdet på Z som härrör från följande uppdelning av två komplexa tal:

Z = (9 - i^två) / (3 + i)

Lösning

Täljaren för uttrycket kan tas med hjälp av följande egenskap:

En skillnad i kvadrater är produkten av summan och skillnaden mellan binomialerna utan kvadrat.

Sedan:

Z = [(3 - i) (3 + i)] / (3 + i)

Det resulterande uttrycket förenklas sedan och lämnar

Z = (3 - i)

Referenser

1. Earl, R. Komplexa nummer. Återställd från: maths.ox.ac.uk.
2. Figuera, J. 2000. Matematik 1: a. Diversifierad. CO-BO-utgåvor.
3. Hoffmann, J. 2005. Urval av matematikämnen. Monfort-publikationer.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Wikipedia. Fantasinummer. Återställd från: en.wikipedia.org