De udda tal är de heltal som inte kan delas med 2. Det betyder att med udda kvantiteter kan du inte skapa grupper om 2, till exempel om någon har 9 godis att dela med en vän och inte vill dela upp någon, kommer en att ha 4 godis och den andra 5.
Några av udda siffror är som följer: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ... I detta uttryck indikerar ellipserna att det finns fler siffror, både till vänster och till höger.
När du tittar noga kan du se att varje udda nummer kan erhållas genom att lägga till 2 till föregående nummer. Om vi till exempel lägger till 2 till -1 får vi 1, om vi gör 1 + 2 får vi 3 och så vidare.
Det observeras också att om paren är sammanflätade, inklusive 0, som betraktas som ett jämnt antal, erhålls uppsättningen heltal Z.
Därför kan alla udda naturliga tal skrivas i formen 2n + 1, där n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, där symbolen ± betyder att n kan tas som positivt eller som negativ.
När det gäller större siffror kan det kännas igen när det är udda, eftersom det alltid slutar på 1, 3, 5, 7 eller 9. Till exempel är 1571 udda och så är det negativa heltalet -152.489.
Artikelindex
Udda nummer förekommer ofta i naturen, och bland dem är siffran 3 av särskild betydelse. Låt oss titta på några exempel:
-Det finns många blommor med ett udda antal kronblad.
-Vi har fem fingrar på varje hand.
-Människor har 23 par kromosomer.
-Det finns de 3 lagarna i Newton och de tre lagarna om termodynamik.
-Atomkärnorna som har ett udda antal protoner och neutroner är mindre stabila än de med ett jämnt antal.
-De vise männen är 3.
-I berättelser och noveller visas nummer 3 ofta, till exempel romaner som De tre musketörerna av Alexander Dumas och i folksagor som De tre bröderna Y De tre små grisarna.
-För konstnärlig komposition finns det så kallade udda regel, vilket fastställer att en komposition med ett udda antal element är mer attraktiv än en med ett jämnt antal. Det udda talet ger dynamik, medan ett jämnt antal ger stabilitet.
-En gemensam strategi för att få priserna på varor att se billigare ut är att få dem att sluta om 9, säg $ 2,99, $ 39 och så vidare..
-Siffran 13 betraktas som otur av vissa, medan andra tillskriver 11 mystiska kvaliteter, båda udda siffror..
Primtal, de som bara erkänner sig själva och 1 som delare, är udda, med undantag av 2, som är det enda jämna primtalet.
Det är möjligt att visa att vilket som helst tal kan sönderdelas som en produkt av primärfaktorer (inklusive kraften hos dessa), och att detta sätt att uttrycka numret är unikt, förutom i faktornas ordning.
Exempelvis kan siffran 45 sönderdelas som 45 = 33 x 5.
Med udda siffror utförs alla aritmetiska operationer, och vissa har framträdande egenskaper.
-Summan av två udda siffror resulterar i ett jämnt tal: 3 + 5 = 8; 11 + 15 = 26; (-10) + (+6) = - 4.
-När du lägger till ett udda tal till ett jämnt tal är resultatet udda: 7 + 2 = 9; 26+ 9 = 35; (-5) + 12 = 7.
-Om n första naturliga, udda och på varandra följande siffrorna är resultatet ntvå. Låt oss titta lite mer detaljerat på detta:
För n = 2: 1 + 3 = 4 = 2två
För n = 3: 1 + 3 + 5 = 9 = 3två
För n = 4: 1 + 3 + 5 + 7 = 16 = 4två
-När ett udda multipliceras med ett jämnt produceras ett jämnt tal: 7 x 4 = 28; (-3) x 12 = -36.
-Att multiplicera två udda siffror ger också en udda: 3 x 5 = 15; (-5) x (+11) = -55.
-När ett positivt tal höjs till en udda effekt, uppstår ett positivt tal, till exempel: 33 = 27.
-När du höjer ett negativt tal till en udda effekt är resultatet negativt: (-2)3= (-2) x (-2) x (-2) = -8.
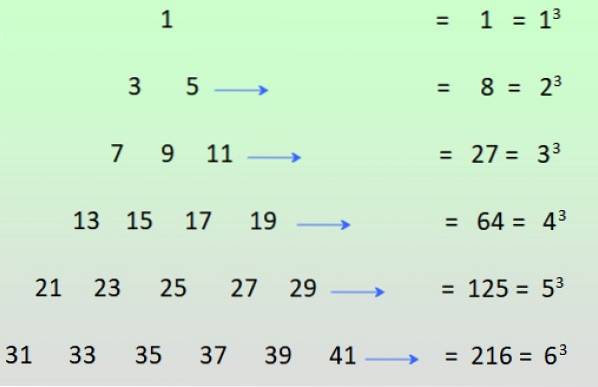
-De udda krafterna hos positiva heltal kan uppnås om udda siffror är ordnade som visas i figuren och raderna läggs till:
Bestäm om resultatet av följande operation är udda eller jämnt:
(53476890083 + 1987628967) x 13567903
För att få svaret behöver du inte springa för att hitta en miniräknare utan snarare tillämpa de synliga egenskaperna. Låt oss titta på de sista siffrorna i tilläggen, som är 3 respektive 7:
53476890083 + 1987628967
Detta betyder att tilläggen är udda och vi vet redan att summan av två udda tal är jämn.
Därför är siffran som härrör från parenteserna jämn och vi kommer att multiplicera den med ett tal som slutar på 3:
13567903
Vilket betyder att detta nummer är udda.
I egenskaperna som beskrivs ovan fastställdes att multiplicering av jämnt x udda resulterar i ett jämnt antal. Därför är den resulterande operationen jämn.
Hur mycket är summan av de första 5 på varandra följande udda siffrorna värd? Hur är det med de första 50??
Summan av de första fem udda numren i rad är:
1 + 3 + 5 + 7 + 9 = 25
Men om vi vill lägga till de första 50 på detta sätt är det besvärligt, så vi går till fastigheterna. De anger att summan av de på varandra följande udda siffrorna är ntvå. I det här fallet är n = 50 och den begärda summan är:
femtiotvå = 50 x 50 = 2500.
När du lägger till tre udda nummer i rad får du 237. Vilka är siffrorna??
Låt oss kalla vårt första udda nummer x, och det andra och z det tredje, enligt uttalandet är det sant att:
x + y + z = 237
På algebraiskt språk kan alla udda tal skrivas i formen 2n +1. Låt oss göra vårt första udda nummer vara:
x = 2n +1
Låt oss lägga till 2 för att få nästa udda:
y = x + 2 = (2n + 1) + 2 = 2n + 3
Och slutligen läggs 2 till igen för att erhålla det tredje udda:
z = (2n +3) + 2 = 2n + 5
Allt detta sammanfattar:
2n + 1 + 2n + 3 + 2n + 5 = 237
6n + 9 = 237
Vilket resulterar i en enkel linjär ekvation, vars lösning är:
n = 38
Och nu med värdet n = 38 finns de tre begärda siffrorna:
x = (2 × 38) + 1 = 77
Följande är därför udda i följd:
y = 79
z = 81
Och läsaren kan enkelt verifiera att summan av de tre är 237.
Ingen har kommenterat den här artikeln än.