
Negativa siffror koncept, exempel, operationer

De negativa siffror är de till vänster om nummerraden, alltid föregångna av ett - tecken. Med hjälp av negativ är det möjligt att representera kvantiteter som är under eller till vänster om 0.
Dessa siffror deltar aktivt i vardagen: om någon till exempel har en skuld på $ 5 men bara kan betala $ 3, är de skyldiga $ 2. Skuld betecknas med ett negativt tecken för att skilja det från det betalade beloppet.
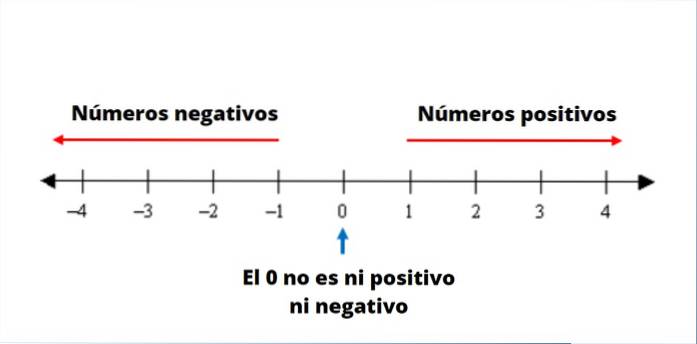
Positioner under havsnivå, temperaturer under vattenets fryspunkt och golv under gatunivå kan betecknas med negativa siffror..
Artikelindex
- 1 Vad är negativa siffror för?
- 2 Operationer med negativa siffror
- 2.1 Absolut värde
- 2.2 Tecken
- 2.3 Summa
- 2.4 Subtraktion
- 2.5 Multiplikation
- 2.6 Uppdelning
- 2.7 Empowerment
- 3 Referenser
Vad är negativa siffror för?
Förekomsten av negativ utökar de möjliga numeriska operationerna. Låt oss ta exemplet med subtraktion av två tal. Om dessa siffror tillhör det naturliga 1, 2, 3, 4, 5 ... är subtraktionen endast meningsfull om det görs genom att subtrahera från ett annat tal som är mindre än det.
Resultatet av operationen 10 - 7 = 3 är rimligt, eftersom vi i princip inte kan ta mer från en mängd än den representerar.
Negativa skulle dock beskriva denna andra situation bra: vi vill köpa något värt $ 20, men vi har bara $ 15 och vi lånar $ 5 från en vän. Skuld, som vi har sagt, är markerad med ett negativt tecken och därmed 15 - 20 = -5, vilket läses som "minus 5".
Uppsättningen av negativa heltal tillsammans med det naturliga och 0 utgör den bredaste uppsättningen heltal Z.
Men negativen kan också vara bråkdelar eller decimaler och tillhör en ännu större uppsättning: den för de verkliga siffrorna R, som inkluderar det rationella och det irrationella..
Med dem alla genomförs de kända aritmetiska operationerna, var noga med att följa några enkla regler för tecken som förklaras nedan.
Negativa nummeroperationer
Innan du utför operationer med negativa siffror måste du skapa några enkla regler för att hantera tecknet (-) som alltid måste förberedas och ordningen på siffrorna.
Tänk på talraden som visas i figuren, med negativ till vänster om 0 och positiva till höger.
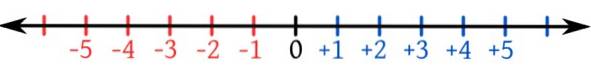
Pilar på sifferraden i båda riktningarna indikerar att det finns oändliga siffror. Observera också att den numeriska uppsättningen heltal är en ordnad uppsättning och alla negativa tal är mindre än 0 och alla positiva tal..
Således är -4 mindre än 1 och -540 är till exempel mindre än 84.
Absolutvärde
Avståndet mellan valfritt nummer och 0 kallas absolutvärde. Detta avstånd är alltid positivt och betecknas med vertikala staplar, så här:
│-5│ = 5
│ + √6│ = √6
│-3 / 4│ = 3/4
│-10,2│ = 10,2
Det vill säga det absoluta värdet av vilket som helst tal, oavsett om det är positivt eller negativt, är det positiva av talet. Detta koncept hjälper oss senare när vi arbetar med negativa siffror.
Tecken
En annan mycket viktig detalj är skillnaden mellan nummertecknet och operationstecknet..
När ett tal är positivt utelämnas vanligtvis tecknet på talet och det är underförstått att det är positivt ändå, men med negativ som inte är möjligt, därför är det nödvändigt att använda parentes, låt oss se:
-Rätt: 17 - (-6) eller även +17 - (-6)
-Felaktigt: 17 - -6
-Fel: -5 + +7
-Rätt: - 5 + (+7) eller även -5 + 7
När begreppen absolut värde, ordning och betydelse av det negativa tecknet är tydliga kan vi gå vidare till de elementära operationerna.
Belopp
Vi skiljer följande fall, med början av summan av två positiva, vars förfarande redan är mycket bekant:
-Lägg till två positiva siffror: (+ a) + (+ b) = a + b
Vilket innebär att vi lägger till som vanligt, låt oss se:
(+8) + (+5) = 8 + 5 = 13
-Lägg till två negativa siffror: (-a) + (-b) = - (a + b)
I det här fallet lägger vi till de absoluta värdena för siffrorna och resultatet läggs fram med ett negativt tecken, så här:
(-7) + (-11) = - (7+ 11) = - 18
-Lägg till ett negativt och ett positivt: (+ a) + (-b)
För denna operation subtraheras de absoluta värdena och resultatet bär tecknet på talet med det högsta absoluta värdet. Låt oss göra några fall:
a) (-16) + (+3)
De respektive absoluta värdena är 16 och 3, siffran med det högsta absoluta värdet är 16, vars tecken är negativt, sedan:
(-16) + (+3) = - (16 - 3) = -13
b) (+8) + (-3) = + (8-3) = +5 = 5
Summan av negativ är också kommutativ, vilket betyder att ordningen på tillägg inte är viktig för resultatet..
De tidigare reglerna gäller om du vill lägga till fler än två nummer, vilket kan göras med den associerande egenskapen: a + b + c = (a + b) + c = a + (b + c).
Innan vi tittar på ett exempel i det här fallet, låt oss först titta på subtraheringen av två heltal.
Subtraktion
Subtraktion definieras som summan av det motsatta. Motsatsen till ett tal a är -a, så här:
-4 är motsatsen till + 4
½ är motsatsen till -½
Om vi ombeds att subtrahera två nummer, oavsett tecknet, lägger vi helt enkelt till motsatsen till det andra till det första:
a) (-53) - (+8) = (-53) + (-8) = - (53 + 8) = -61
b) (+7) - (-12) = (+7) + (+12) = 7 + 12 = 19
c) (+2) - (+ π) = (+2) + (-π) = 2 - π
Exempel
Utför följande operation (+4) + (-7) + (+19)
Vi skriver om det så här med hjälp av parenteser för att indikera den operation som ska utföras först:
(+4) + (-7) + (+19) = [(+4) + (-7)] + (+19) = [- (4-7)] + 19 = [- (-3)] + 19 = 19 - (-3) = 19 + (+3) = 22
Multiplikation
Regeln om tecken för multiplikation sammanfattas i följande figur:
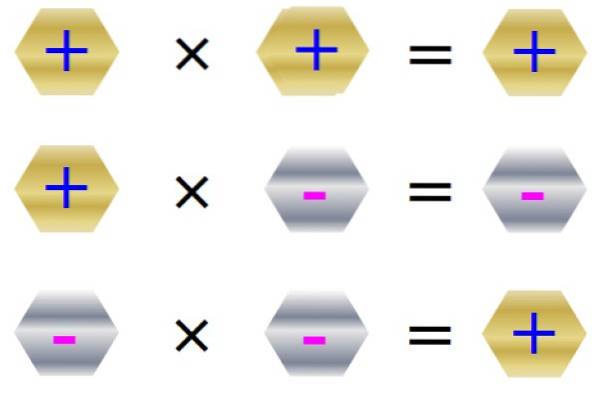
Multiplikationens egenskaper
-Kommutativitet: Faktornas ordning förändrar inte produkten, därför är ≠ = b.a där a och b är negativa, heltal eller bråktal.
-Associativitet: Låt a, b och c vara heltal, det är sant att (a.b). c = a. (före Kristus)
-Distributivitet med avseende på summan: låt a, b och c vara heltal, det är giltigt att a. (b + c) = a.b + a.c
Exempel
(-3/2) x [(-5) + (+4) - (+2)] = (-3/2) x (-5) + (-3/2) x (+4) + (- 3/2) x (-2) = (15 - 12 + 6) / 2 = 9/2
Du kan också ha löst operationen inom parentes först och multiplicera resultatet med (-3/2), så här:
(-3/2) x [-5 + 4 - 2] = (-3/2) x (-3) = 9/2
Division
Regeln för tecken för delning visas i följande bild:
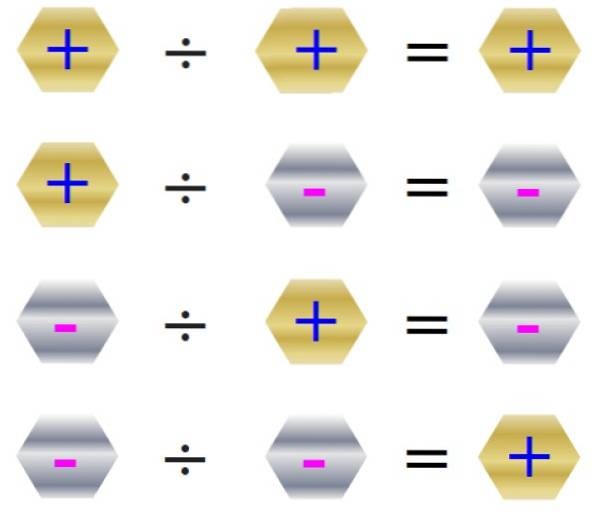
Uppdelning är inte kommutativ och vanligtvis a ÷ b ≠ b ÷ a, delning med 0 är inte tillåten. Låt oss se ett exempel:
(-54) ÷ (+3) = -18
För att uppnå detta resultat gör du helt enkelt kvoten och tecknet väljs enligt tabellen som visas i figuren, vilket motsvarar det tredje alternativet från topp till botten.
Bemyndigande
Empowerment är driften av formen an, där a är basen och n är exponenten. Basen och exponenten kan ha vilket tecken som helst.
-Om basen är negativ eller positiv och exponenten är ett jämnt heltal är resultatet av operationen alltid positivt.
-När basen är positiv och exponenten är ett udda heltal är resultatet positivt.
-Och om basen är negativ och exponenten är ett udda heltal är resultatet negativt.
Fraktionerade exponenter uttrycks alternativt som en rot, till exempel är en kvadratrot ekvivalent med den fraktionerade exponenten ½, en kubrot motsvarar exponenten 1/3 och så vidare.
Låt oss titta på några exempel:
a) (-3)3 = (-3) x (-3) x (-3) = -27
b) 16 -1/2 = 1 / √16 = ¼
c) (+8) 1/3 = kubrot av 8 = 2
Referenser
- Baldor, A. 1986. Aritmetik. Codex-utgåvor och distributioner.
- Figuera, J. 2000. Matematik 7: e. Kvalitet. CO-BO-utgåvor.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematik är kul. Hur man lägger till och subtraherar positiva och negativa siffror. Återställd från: mathisfun.com
- Wikipedia. Negativa siffror. Återställd från: es.wikipedia.org.



Ingen har kommenterat den här artikeln än.