De endimensionella vågor De är de som sprider sig i en enda riktning oavsett om vibrationer sker i samma riktning för förökning eller inte. Ett bra exempel på dem är vågen som färdas genom en stram sträng som en gitarr..
I en platt våg korsa, partiklarna vibrerar i vertikal riktning (de går upp och ner, se den röda pilen i figur 1), men den är endimensionell eftersom störningen bara går i en riktning efter den gula pilen.
Endimensionella vågor uppträder ganska ofta i vardagen. I följande avsnitt beskrivs några exempel på dem och även på vågor som inte är endimensionella för att tydligt fastställa skillnaderna.
Artikelindex
Här är några exempel på endimensionella vågor som lätt kan observeras:
- En ljudpuls som färdas genom en rak bar, eftersom det är en störning som förökar hela stapelns längd.
- En våg som går genom en vattenkanal, även om förskjutningen av vattenytan inte är parallell med kanalen.
- Vågor som sprider sig på en yta eller genom ett tredimensionellt utrymme kan också vara endimensionella, så länge deras vågfronter är plan parallella med varandra och bara rör sig i en riktning..
Ett exempel på en icke-dimensionell våg finns i vågor som bildas på en stilla vattenyta när en sten tappas. Det är en tvådimensionell våg med en cylindrisk vågfront.
Ett annat exempel på en icke-dimensionell våg är ljudvågen som en smällare genererar genom att explodera i en viss höjd. Detta är en tredimensionell våg med sfäriska vågfronter.
Det mest allmänna sättet att uttrycka en endimensionell våg som sprider sig utan dämpning i axelns positiva riktning x och med hastighet v är, matematiskt:
y (x, t) = f (x - v.t)
I detta uttryck Y representerar störningen i positionen x Omedelbart t. Vågens form ges av funktionen F. Till exempel är vågfunktionen som visas i figur 1: y (x, t) = cos (x - v t) och vågbilden motsvarar ögonblicket t = 0.
En våg som denna, beskriven av en cosinus eller sinusfunktion, kallas harmonisk våg. Även om det inte är den enda vågformen som finns, är den av yttersta vikt, eftersom alla andra vågor kan representeras som en superposition eller summan av harmoniska vågor. Det handlar om det kända Fourier-sats, så används för att beskriva signaler av alla slag.
När vågen färdas i x-axelns negativa riktning ändras den helt enkelt v för -v i argument, lämnar:
y (x, t) = g (x + v t)
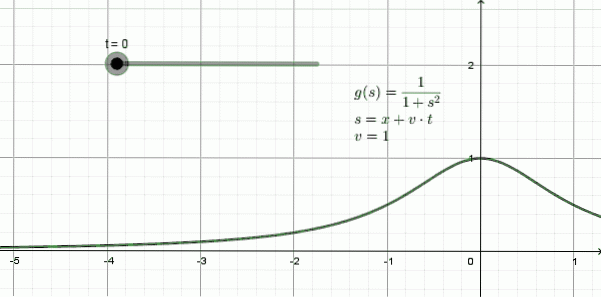
Figur 3 visar animationen för en våg som rör sig åt vänster: det är en form som kallas en funktion lorentziana och henne matematiskt uttryck är:
y (x, t) = 1 / (1 + (x + 1)⋅t)två
I detta exempel är fortplantningshastigheten v = 1, -en enhet för varje tidsenhet-.
Vågekvationen är en partiell derivatekvation, vars lösning naturligtvis är en våg. Den fastställer det matematiska förhållandet mellan den rumsliga delen och den temporala delen av den och har formen:
Följande är det allmänna uttrycket y (x, t) för en harmonisk våg:
y (x, t) = A⋅cos (k⋅x ± ω⋅t + θo)
a) Beskriv den fysiska betydelsen av parametrarna A, k, ω Y θo.
b) Vilken mening har ± tecknen i cosinusargumentet?
c) Kontrollera att det givna uttrycket verkligen är lösningen på vågekvationen från föregående avsnitt och hitta hastigheten v fortplantning.
Vågens egenskaper finns i följande parametrar:
-TILL representerar amplitud eller "våghöjd".
-vad är i vågnummer och är relaterad till våglängden λ genom k = 2π / λ.
-ω är fvinkelfrekvens och är relaterad till period T vågoscillation av
ω = 2π / T.
-θo är inledande fasen, som är relaterad till vågens startpunkt.
Ett negativt tecken tas om vågen färdas i X-axelns positiva riktning och ett positivt tecken annars..
Kontrollera att det givna uttrycket är en lösning av vågekvationen är enkel: det delvisa derivatet av funktionen tas y (x, t) med avseende på x två gånger, delvis re-derivat med avseende på t två gånger, och kombinera sedan båda resultaten för att få en jämlikhet:
Andra derivat med avseende på x: ∂tvåy / ∂xtvå= -Ktvå. TILL⋅cos (k⋅x ± ω⋅t + θo)
Andra derivat med avseende på t: ∂tvåy / ∂ttvå= -Ωtvå. TILL⋅cos (k⋅x ± ω⋅t + θo)
Dessa resultat ersätts i vågekvationen:
-ktvå. TILL⋅cos (k⋅x ± ω⋅t + θo) = (1 / vtvå) (-ωtvå. TILL⋅cos (k⋅x ± ω⋅t + θo))
Så mycket TILL eftersom cosinus förenklas, eftersom de förekommer på båda sidor av jämställdheten och cosinusens argument är detsamma, reduceras därför uttrycket till:
-ktvå = (1 / vtvå) (-ωtvå)
Som gör det möjligt att få en ekvation för v i form av ω Y k:
vtvå = ωtvå / ktvå
v = ± ω / k
Ingen har kommenterat den här artikeln än.