
Lutning av en linjeformel och ekvationer, representation, exempel
De lutning på en linje är tangenten för vinkeln θ som linjen bildar med den horisontella axeln, vilken enligt konvention mäts moturs. Lutningen på vilken linje som helst är alltid konstant och det är därför det är en av dess viktigaste egenskaper..
För att beräkna det måste du känna till två punkter på raden, vars koordinater är (x1,Y1) och (xtvå,Ytvå). Ett segment som tillhör linjen ritas mellan båda punkterna och sedan ritas segmenten som representerar avståndet mellan x.1 och xtvå, och mellan och1 och ochtvå, som i figuren nedan.
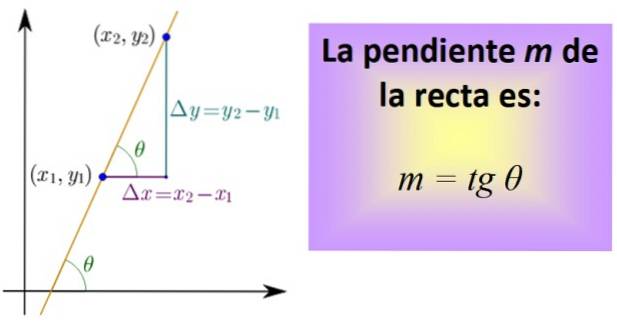
De tre segmenten utgör en höger triangel vars ben är: Δx = xtvå - x1 y Ay = ytvå - Y1. De motsvarar en horisontell respektive en vertikal förskjutning..
Nu definierar vi en kvot, kallad tangent för vinkeln θ och förkortad tg θ, vilket är precis lutningen m av den raka:
m = tg θ = Ay / Ax
Observera att för en linje förblir denna vinkel konstant, oavsett vilka punkter som tas för att beräkna dess tangent. I vilket fall som helst ger detta värde oss ett mått på hur brant linjen är.
Genom koordinaterna för de valda punkterna är formeln för lutningen:
m = (y - y1 ) / (xtvå - x1)
Artikelindex
- 1 Grafisk representation
- 2 typer av lutning
- 3 Hur beräknar du linjens lutning?
- 4 Lösta övningar
- 4.1 - Övning 1
- 4.2 - Övning 2
- 5 Exempel
- 5.1 Exempel 1
- 5.2 Exempel 2
- 6 Referenser
Grafisk representation
Nedan har vi flera situationer där begreppet lutning är relevant. Dess värde kan enkelt beräknas genom att mäta respektive vertikal och horisontell förskjutning och sedan göra kvoten som anges i början.
Detta ger oss en uppfattning om ojämnheten eller nedgången i någon struktur, såsom en ramp, ett tak eller en väg:
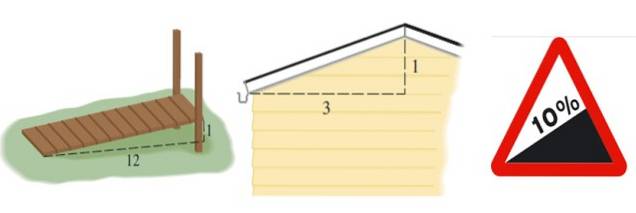
Lutningen på rampen som visas i figur 2 till vänster är m = 1/12, takets m är 1/3 och vägens väg uttrycks i procent. En procentsats på 10% innebär att för varje 100 meter som går horisontellt går 10 meter i höjd:
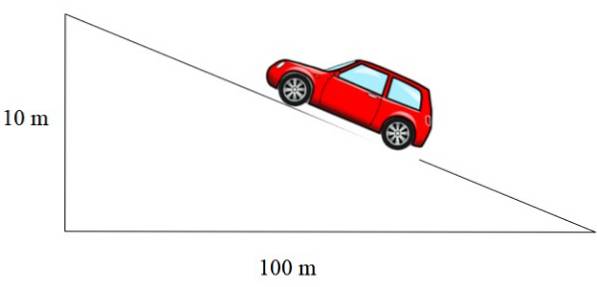
I detta fall är lutningen 10/100 = 0,1, vilket, uttryckt i procent, är lika med 10%..
Lutningstyper
Lutningen på en linje kan vara positiv, negativ eller noll. Till exempel har linjen som visas i figur 1 en positiv lutning. Vi uppskattar det omedelbart eftersom vi ser att linjen "stiger" om vi ser den från vänster till höger.
Om linjen sjunker från vänster till höger är dess lutning negativ. Och när en linje är horisontell är dess lutning noll.
Slutligen definieras lutningen inte för vertikala linjer.
Den grafiska representationen av varje typ är nedan:
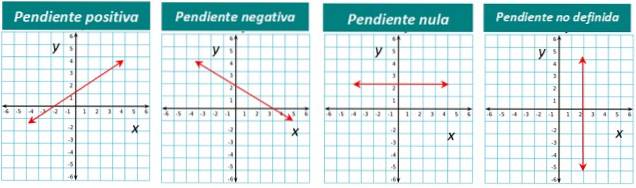
Hur beräknar man linjens lutning?
Beräkningen av lutningen är väldigt enkel, du behöver bara hitta den vertikala förskjutningen och den horisontella förskjutningen och sedan göra kvoten mellan båda.
När vi har ritat linjen i det kartesiska planet, hittas dessa förskjutningar genom att välja två punkter på linjen P1 Och stvå, bestämma dess koordinater och tillämpa definitionen i början:
m = (y - y1 ) / (xtvå - x1 )
Eftersom lutningens värde är oberoende av valet av P1 Och stvå , vi ska välja en punkt P någon av koordinaterna (x, y) som tillhör linjen, vars koordinater inte är kända, och en annan punkt P1 vars koordinater är: (x1,Y1).
Lutningen är:
m = (y - y1) / (x - x1)
Vi kan rensa Y:
och och1 = m (x - x1)
Antag nu att punkten P1 är skärningspunkten mellan linjen och den vertikala axeln för koordinaterna (0, b). Att ersätta detta i ovanstående ekvation:
y - b = m (x - 0) → y = mx + b
Detta uttryck är känt som linjens ekvation i formen lutning - fånga, eftersom linjen bestäms otvetydigt när dess lutning och dess skärningspunkt med den vertikala axeln är kända.
Att bara känna till lutningen räcker inte för att karakterisera en linje i planet, eftersom oändliga linjer kan ha samma lutning, vilket innebär att de är parallella, men passerar genom andra punkter.
Lösta övningar
- Övning 1
Hitta lutningen på linjen som visas i följande bild:
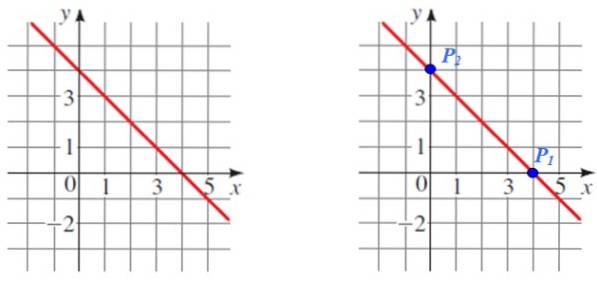
Lösning
P1 Och stvå är två lättlästa punkter som kommer att användas för beräkningen, notera också att de är respektive korsningar med koordinataxlarna.
Koordinaterna för varje punkt är:
P1 (4.0) och Ptvå (0,4)
Genom att ersätta lutningen i ekvationen:
m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1
Lutningen är negativ, vilket man kunde förvänta sig efter att ha tittat på diagrammet.
- Övning 2
Hitta ekvationen för linjen som passerar genom punkten (1, -6) och är parallell med linjen y = 2x - 3.
Lösning
Lutningen på den sökta linjen måste vara densamma som y = 2x - 3, eftersom de är parallella. För denna linje är lutningen m = 2, därför har den vi letar efter formen:
och och1 = 2 (x - x1)
Nu ersätter vi den punkt genom vilken vår linje passerar: x1 = 1 och y1 = -6.
y - (-6) = 2 (x - 1)
Därför är y = 2x - 2 - 6 → y = 2x - 8
Exempel
Två kvantiteter kan relateras på ett sådant sätt att deras diagram är en rak linje. I så fall sägs det att mängderna har linjärt beroende och linjens lutning kan tolkas som förändringshastigheten från en variabel till en annan.
Exempel 1
Anta att en pool är fylld med vatten vid en Betygsätta konstant i tid. Naturligtvis ju mer tid som går desto mer lagras vatten. Tja, den takt med vilken poolen fylls är exakt lutningen på linjen som relaterar volymen till tiden:
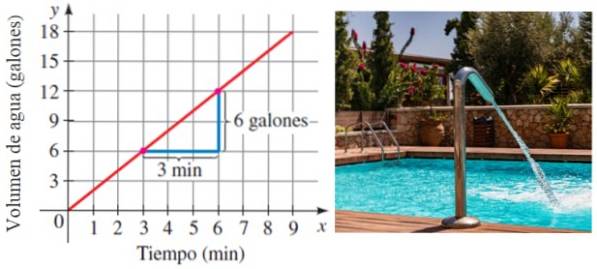
I detta exempel fylls poolen med en hastighet av 6/3 gallon per minut eller 2 gallon / minut.
Exempel 2
När en mobil rör sig i en rak linje med konstant hastighet är lutningen för positionsdiagrammet som en funktion av tiden ingen annan än nämnda hastighet. Grafen visar en mobil med positiv hastighet, vilket innebär att den rör sig bort från ursprunget.
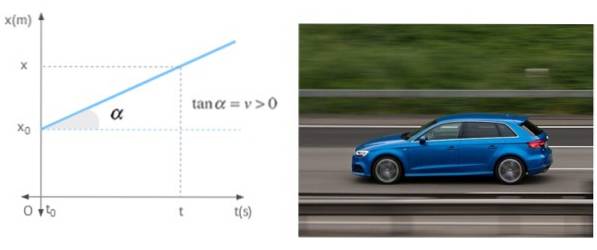
Referenser
- Alvarez, J. Lutningen på en motorväg. Återställd från: geogebra.es.
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Hoffman, J. Selection of Mathematics Topics. Volym 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalculus: Matematik för Calculus. 5: e. Utgåva. Cengage Learning.
- Zill, D. 1984. Algebra och trigonometri. Mcgraw hill.

Ingen har kommenterat den här artikeln än.