
Vikt (fysik) beräkning, enheter, exempel, övningar

De vikt det är den kraft med vilken jorden drar objekt till sin yta. Varje gång ett objekt tappas faller det till marken, det kan inte klättra på egen hand, och det är inte heller tyngt halvvägs, vilket beror på att jorden lockar det..
Alla föremål lockar alltid varandra, även de minsta, bara storleken på den kraft som de gör är proportionell mot massan. Detta innebär att föremål med liten massa utövar liten kraft på andra, men himmelskroppar som jorden kan utöva en mycket stor kraft..
Jorden håller månen i omlopp tack vare denna attraktiva kraft, som kallas gravitationell attraktion när det gäller föremål som ligger långt från jordytan, och vikt när föremål är nära.
Av detta följer att tyngdkraften inte kräver att föremål nödvändigtvis är i kontakt med varandra för att kunna agera: det är därför det sägs vara en verkningskraft på avstånd.
Föremål fortsätter att ha vikt även om de ligger i en viss höjd över marken och ju mer massiva de är, desto större blir denna vikt.
Den stora engelska forskaren Isaac Newton var den första som gav en förklaring om denna fråga genom den allmänna gravitationslagen som bär hans namn och som sedan dess har tjänat till att förstå hur objekt med massa interagerar. Detta är mycket viktigt, eftersom alla objekt på planeten har vikt.
Artikelindex
- 1 vikt enheter
- 1.1 Kilokraften
- 1.2 Pundkraften
- 2 Viktberäkning och formel
- 3 Vikt som vektor
- 4 Skillnader mellan vikt, massa och volym
- 5 Viktexempel
- 6 Övningen löst
- 7 Referenser
Enheter av vikt
Det internationella systemet för SI-enheter har som en vikt för enheten Newton, uppkallad efter Isaac Newton. Detta är enheten för att mäta krafter av alla slag.
Newton, förkortat N, definieras som den kraft som krävs för ett objekt med en massa på 1 kg för att få en acceleration på 1 m / stvå. Förutom Newton finns det andra kraftenheter som är vanligt förekommande, till exempel följande:
Kilogramkraften
De kilo-kraft eller kilopond, förkortat kg-f eller kp, även om det vanligtvis kallas kg utan mer, är den kraft som jorden utövar på ett föremål som ligger vid havsnivå och vid 45 ° nordlig latitud. Det är nödvändigt att ange platsen, eftersom gravitationsfältet som sagt upplever variationer med höjd och latitud.
När någon säger att han väger 45 kg, menar han egentligen att hans vikt är 45 kg-f, eftersom kilogrammet är den enhet som är reserverad för massa.
Ekvivalensen mellan kg-f och N är: 1 kg-f = 9,8 N
Pund-kraft
De pund-kraft, förkortad lb-f är också en kraftenhet som är analog med kg-f, eftersom det är den kraft som jorden utövar på ett objekt med en massa massa. Och som med kg-f finns det inga problem med värdena när du befinner dig på jorden, det vill säga ett massföremål l lb, väger 1 lb-f.
Ekvivalensen i lb-f och N är: 1 lb-f ≡ 4.448222 N.
Viktberäkning och formel
Ett objekts vikt är proportionell mot dess massa. Ju större massa, desto större vikt.
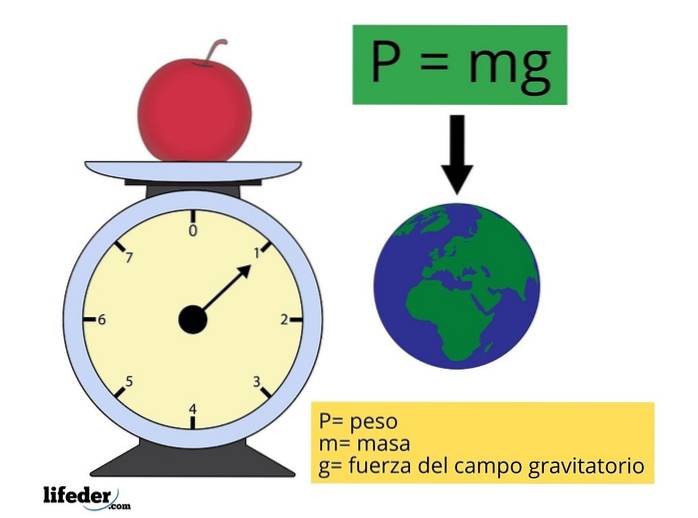
Formeln för att hitta storleken på vikten P (eller även W, som det ibland betecknas, med "Vikt" på engelska) är mycket enkelt:
P = mg
Var m representerar objektets massa och g är storleken på tyngdaccelereringen (gravitationsfältets eller gravitationens intensitet), ungefär konstant och vars värde tas som 9,81 m / stvå för de vanligaste beräkningarna.
Vikt är en vektor och djärva bokstäver används för att skilja mellan en vektor och dess storlek. På detta sätt, när man talar om P, förstås att det är det numeriska värdet och när det är skrivet P hänvisning görs till vektorn:
P = m ∙g
De g i fetstil är jordens gravitationsfält, det vill säga det inflytande som jorden utövar på utrymmet som omger det, oavsett om det finns någon annan kropp som uppfattar det eller inte. Varje objekt med massa har sitt eget gravitationsfält, vare sig det är litet eller stort.
Intensiteten i jordens gravitationsfält g det är inte helt konstant. Det har små variationer som uppstår främst för att jorden inte är en perfekt sfär och också på grund av lokala höjd- och densitetsskillnader. Men för de flesta applikationer är värdet 9,81 m / stvå Det fungerar väldigt bra.
Andra himlakroppar har sina egna karaktäristiska gravitationsfält, därför varierar tyngdaccelerationen beroende på planet eller satellit. Samma objekt skulle ha olika vikt i var och en, därför är vikt inte en karakteristisk egenskap hos saker, utan materia i allmänhet..
Vikt som vektor
Vikt är en vektor och har därför storlek, riktning och känsla. I närheten av jordytan är vikten en vektor i vertikal riktning och riktningen är alltid nere.
Vanligtvis benämns den vertikala riktningen som axeln Y eller z, och riktningen nedåt tilldelas ett + eller - tecken för att skilja den från uppåtgående riktning. Valet beror på platsen för ursprunget. I bilden nedan valdes ursprunget vid den punkt från vilken äpplet faller:
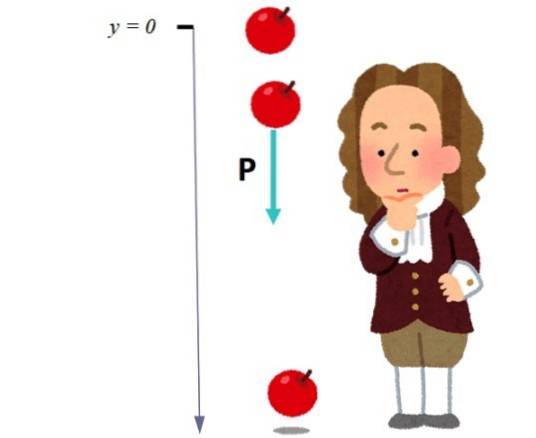
Enhetsvektorn j, en vektor med en storlek lika med 1 används för att markera och skilja den vertikala riktningen. När det gäller denna vektor skrivs vikten så här:
P = mg (- j)
Där negativt tecken tilldelas nedåtgående riktning.
Skillnader mellan vikt, massa och volym

Dessa tre begrepp är ofta förvirrade, men genom att granska viktens egenskaper är det lätt att skilja det från massa och volym..
Till att börja med beror vikten på gravitationsfältet där objektet är. Till exempel, på jorden och på månen har samma sak en annan vikt, även om antalet atomer som komponerar den förblir konstant..
Massa är en skalär kvantitet, relaterad till antalet atomer som utgör objektet och framgår av motståndet att objektet måste ändra sin rörelse, en egenskap som kallas tröghet.
För sin del är volymen måttet på det utrymme som ett objekt upptar, en annan skalär kvantitet. Två objekt med samma volym väger inte samma, till exempel väger en järnkub mycket mer än en polystyrenkub med samma dimensioner.
Sammanfattningsvis:
- Massa är relaterad till mängden materia som en kropp har.
- Vikt är den kraft som jorden utövar på denna massa, proportionell mot den.
- Volym är det utrymme som materien upptar.
Det bör noteras att det att vara skalära kvantiteter har varken massa eller volym riktning eller känsla, utan endast numeriskt värde och en adekvat enhet. Å andra sidan måste vikten, som är en vektor, alltid uttryckas korrekt som anger storleken, enheten, riktningen och känslan, som i föregående avsnitt.
Viktexempel
Alla objekt på jorden har vikt, du kan till och med "väga" föremål som inte finns på jorden, till exempel andra planeter eller solen, men naturligtvis med indirekta medel.
Eftersom viktsområdet är mycket stort används vetenskaplig notation (i styrkorna 10) för att uttrycka några som är mycket stora eller mycket små:
-Solen: 1 989 × 1030 kg-f
-Jupiter: 1 898 × 1027 kg-f
-En mygga: 2,0 × 10-5 N
-Spädbarn: 34,3 N
-Ett barn: 353 N.
-Vuxen person: 65 kg-f
-En vuxen elefant: 5,5 × 103 kg-f
-Blåval: 1,0 × 106 N
Övningen löst
En låda med massa 20 kg vilar på ett bord.
a) Hitta lådans vikt och den normala kraft som tabellen utövar på den.
b) Ytterligare en 10 kg låda placeras ovanpå den första. Hitta det normala som bordet utövar på 20 kg lådan och det normala som detta utövar på den mindre lådan.
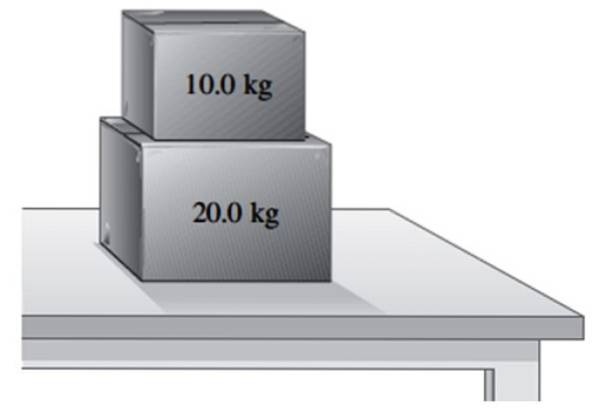
Lösning till
Det är bekvämt att skapa ett fritt kroppsdiagram på lådan, som består av att rita de krafter som verkar på den.
I den här situationen är den minsta lådan inte på toppen ännu, därför finns det bara två krafter: den första är vikt. P som dras vertikalt nedåt, som anges i föregående avsnitt och sedan finns det normala N, vilket är den vinkelräta kraften som utövas av bordet och förhindrar att lådan faller.
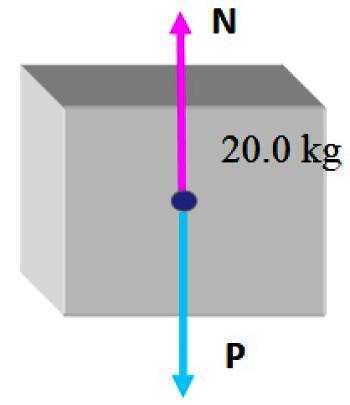
Med tanke på att lådan är i statisk jämvikt under dessa förhållanden är det rimligt att dra slutsatsen att normalens storlek är densamma som vikten, så att den kan kompensera, därför:
N = mg = 20,0 kg x 9,8 m / stvå = 196 N; riktas vertikalt uppåt.
För sin del är vikten P = 196 N riktad vertikalt nedåt.
Lösning b
Nu skapas nya fria kroppsdiagram på båda föremålen. För den stora rutan förändras saker lite, eftersom den lilla rutan utövar kraft på den.
Krafterna är som följer: N Y P är det normala som utövas av tabellen och vikten på lådan på 20,0 kg, som inte förändrades. Och den nya kraften som utövas av den lilla lådan är N1, normalt på grund av kontakt med den stora lådans överyta.
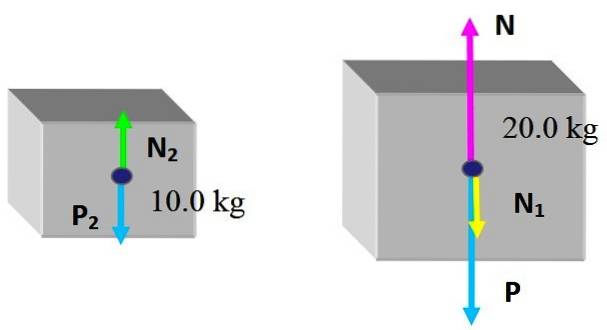
När det gäller den lilla lådan får den det normala Ntvå, utövas av den stora lådans övre yta och naturligtvis dess vikt Ptvå. Eftersom lådorna är i statisk jämvikt:
Ntvå - Ptvå = 0
N - N1 - P = 0
Från den första ekvationen har vi den Ntvå = Ptvå = 10 kg x 9,8 m / stvå = 98 N. Enligt handlings- och reaktionslagen är storleken på den kraft som den lilla lådan får samma som den utövar på den stora lådan, sedan:
Ntvå = N1 = 98 N
Från den andra ekvationen rensas den normala N som utövas av tabellen på den stora rutan, som i sin tur har den lilla rutan ovanpå:
N = N1 + P = 98 N + 196 N = 294 N
Referenser
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Volym 2. Dynamik. Redigerad av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Red. Volym 1. Pearson.
- Serway, R., Jewett, J. 2008. Fysik för vetenskap och teknik. Volym 1. 7: e. Ed. Cengage Learning.
- Thomas Griffith, W. 2007. Konceptuell fysik. Mc Graw Hill.


Ingen har kommenterat den här artikeln än.