
Elektrisk potentialformel och ekvationer, beräkning, exempel, övningar
De elektrisk potential den definieras vid vilken punkt som helst där ett elektriskt fält existerar som den potentiella energin för detta fält per laddningsenhet. Punktladdningar och punkt- eller kontinuerliga laddningsfördelningar producerar ett elektriskt fält och har därför en tillhörande potential.
I det internationella systemet för enheter (SI) mäts den elektriska potentialen i volt (V) och betecknas som V. Matematiskt uttrycks den som:
V = U / qeller

Där U är den potentiella energin förknippad med laddningen eller fördelningen och qeller det är en positiv testladdning. Eftersom U är en skalär, så är potentialen också.
Från definitionen är 1 volt helt enkelt 1 Joule / Coulomb (J / C), där Joule är SI-enheten för energi och Coulomb (C) är enheten för elektrisk laddning..
Antag att en punktladdning q. Vi kan kontrollera vilken typ av fält som denna laddning producerar genom att använda en liten, positiv testladdning, kallad qeller, används som sond.
Arbetet W behövde flytta denna lilla last från punkten till tills poängen b, är det negativa av skillnaden mellan potentiell energi ΔU mellan dessa punkter:
Wa → b = -AU = - (Ub - ELLERtill)
Dela upp allt mellan qeller:
Wa → b / qeller= - ΔU / qeller = - (Ub - ELLERtill) / qeller = - (V.b - Vtill) = -AV
Här Vb är potentialen vid punkt b och V.till är det i punkt a. Den potentiella skillnaden Vtill - Vb är potentialen i om b och kallas Vab. Ordningen på prenumerationerna är viktig, om den ändrades skulle den representera potentialen för b med avseende på a.
Artikelindex
- 1 Elektrisk potentialskillnad
- 1.1 Tecken och värden för den potentiella skillnaden
- 2 Hur man beräknar den elektriska potentialen?
- 2.1 Elektrisk potential för diskret laddningsfördelning
- 2.2 Elektrisk potential vid kontinuerlig belastningsfördelning
- 3 Exempel på elektrisk potential
- 3.1 Batterier och batterier
- 3.2 Strömuttag
- 3.3 Spänning mellan laddade moln och marken
- 3.4 Van Der Graff-generator
- 3.5 Elektrokardiogram och elektroencefalogram
- 4 Övningen löst
- 4.1 Lösning a
- 4.2 Lösning b
- 4.3 Lösning c
- 4.4 Lösning d
- 4.5 Lösning e
- 4.6 Lösning f
- 5 Referenser
Elektrisk potentialskillnad
Av det föregående följer att:
-AV = Wa → b / qeller
Därför:
AV = -Wa → b / qeller
Nu beräknas arbetet som integralen i den skalära produkten mellan den elektriska kraften F mellan q och qeller och förskjutningsvektorn dℓ mellan punkterna a och b. Eftersom det elektriska fältet är kraft per laddningsenhet:
OCH = F/ qeller
Arbetet med att bära testbelastningen från a till b är:
Denna ekvation ger möjlighet att direkt beräkna potentialskillnaden om laddningens elektriska fält eller distributionen som producerar den tidigare är känd..
Och det noteras också att potentialskillnaden är en skalär kvantitet, till skillnad från det elektriska fältet, som är en vektor.
Tecken och värden för den potentiella skillnaden
Från den tidigare definitionen observerar vi att om OCH och dℓ är vinkelräta, är potentialskillnaden AV noll. Detta betyder inte att potentialen vid sådana punkter är noll, utan att helt enkelt Vtill = Vb, det vill säga potentialen är konstant.
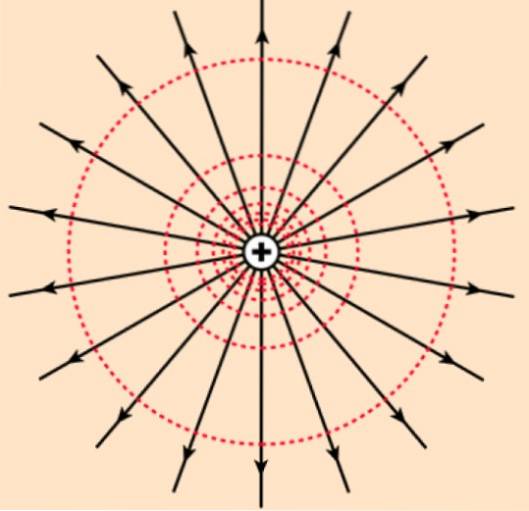
Linjerna och ytorna där detta händer kallas potential. Till exempel är de ekvipotentiella linjerna i fältet för en punktladdning omkretsar koncentriska till laddningen. Och de ekvipotentiella ytorna är koncentriska sfärer.
Om potentialen produceras av en positiv laddning, vars elektriska fält består av radiella linjer som projicerar laddningen, när vi rör oss bort från fältet blir potentialen mindre och mindre. Som testbelastning qeller är positiv, du känner mindre elektrostatisk avstötning ju längre du är från q.

Tvärtom, om lasten Vad är negativ, testladdningen qeller (positivt) kommer att ha en lägre potential när det kommer närmare Vad.
Hur man beräknar den elektriska potentialen?
Integralen som ges ovan tjänar till att hitta potentialskillnaden och därmed potentialen vid en given punkt b, om referenspotentialen är känd vid en annan punkt till.
Till exempel finns det en punktbelastning Vad, vars elektriska fältvektor vid en punkt som ligger på avstånd r av lasten är:
OCH = kq / rtvå r
Där k är den elektrostatiska konstanten vars värde i internationella systemenheter är:
k = 9 x 10 9 Nmtvå / Ctvå.
Och vektorn r är enhetsvektorn längs linjen som sammanfogar Vad med punkt P.
Det ersätts i definitionen av AV:

Väljer den punkten b vara på avstånd r av laddningen och att när a → ∞ är potentialen 0, då Vtill = 0 och föregående ekvation är som:
V = kq / r
Välj Vtill = 0 när a → ∞ är vettigt, för vid en punkt långt ifrån lasten är det svårt att inse att den existerar.
Elektrisk potential för diskreta laddningsfördelningar
När det finns många poängladdningar fördelade i ett område beräknas den elektriska potential som de producerar vid varje punkt P i rymden, vilket adderar de individuella potentialer som var och en producerar. A) Ja:
V = V1 + Vtvå + V3 +… VN = ∑ Vi
Summationen sträcker sig från i = till N och potentialen för varje laddning beräknas med hjälp av ekvationen i föregående avsnitt.
Elektrisk potential vid kontinuerlig belastningsfördelning
Med utgångspunkt från potentialen för en punktladdning kan vi hitta den potential som produceras av ett laddat objekt, med en mätbar storlek, när som helst P.
För att göra detta är kroppen uppdelad i många små oändliga laddningar dq. Var och en bidrar till den fulla potentialen med en dV oändligt liten.

Sedan läggs alla dessa bidrag till genom en integral och därmed uppnås den totala potentialen:

Exempel på elektrisk potential
Det finns elektrisk potential i olika enheter tack vare vilka det är möjligt att få elektrisk energi, till exempel batterier, bilbatterier och eluttag. Elektriska potentialer etableras också i naturen under elektriska stormar.
Batterier och batterier
I celler och batterier lagras elektrisk energi genom kemiska reaktioner inuti dem. Dessa inträffar när kretsen är stängd, vilket gör att likström kan strömma och en glödlampa tänds eller bilens startmotor fungerar..
Det finns olika spänningar: 1,5 V, 3 V, 9 V och 12 V är de vanligaste.
Utlopp
Hushållsapparater och apparater som drivs med kommersiell nätström är anslutna till ett vägguttag. Beroende på plats kan spänningen vara 120 V eller 240 V.

Spänning mellan laddade moln och marken
Det är den som inträffar under elektriska stormar på grund av den elektriska laddningens rörelse genom atmosfären. Det kan vara i storleksordningen 108 V.

Van Der Graff generator
Tack vare ett gummitransportband skapas friktionsladdning som ackumuleras på en ledande sfär placerad ovanpå en isoleringscylinder. Detta genererar en potentiell skillnad som kan vara flera miljoner volt.

Elektrokardiogram och elektroencefalogram
I hjärtat finns specialiserade celler som polariserar och depolariserar, vilket orsakar potentiella skillnader. Dessa kan mätas som en funktion av tiden med hjälp av ett elektrokardiogram..
Detta enkla test utförs genom att placera elektroder på personens bröst, som kan mäta små signaler..
Eftersom de är mycket låga spänningar måste du förstärka dem bekvämt och sedan spela in dem på ett pappersband eller titta på dem genom datorn. Läkaren analyserar pulsen för avvikelser och upptäcker därmed hjärtproblem.

Hjärnans elektriska aktivitet kan också registreras med ett liknande förfarande, kallat EEG..
Övningen löst
En last F = - 50,0 nC ligger 0,30 m från punkten TILL och 0,50 m från punkt B, som visas i följande bild. Svara på följande frågor:
a) Vad är potentialen i A som produceras av denna laddning?
b) Och vad är potentialen i B?
c) Om en laddning q rör sig från A till B, vad är den potentiella skillnaden genom vilken den rör sig?
d) Ökar eller minskar potentialen enligt föregående svar??
e) Om q = - 1,0 nC, vad är förändringen i dess elektrostatiska potentialenergi när den rör sig från A till B?
f) Hur mycket arbete gör det elektriska fältet som produceras av Q när testladdningen rör sig från A till B?

Lösning till
Q är en punktladdning, därför beräknas dess elektriska potential i A av:
VTILL = kQ / rTILL = 9 x 109 x (-50 x 10-9) / 0,3 V = -1500 V
Lösning b
På samma sätt
VB = kQ / rB = 9 x 109 x (-50 x 10-9) / 0,5 V = -900 V
Lösning c
AV = Vb - Vtill = -900 - (-1500) V = + 600 V.
Lösning d
Om laddningen q är positiv ökar potentialen, men om den är negativ, minskar dess potential.
Lösning e
AV = AV / qeller → ΔU = qeller AV = -1,0 x 10-9 x 600 J = -6,0 x 10-7 J.
Det negativa inloggningen UU indikerar att den potentiella energin i B är mindre än A.
Lösning f
Eftersom W = -ΔU realiseras fältet +6,0 x 10-7 J av arbetet.
Referenser
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 5. Elektrostatik. Redigerad av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.
- Resnick, R. (1999). Fysisk. Vol. 2. 3: e upplagan på spanska. Compañía Editorial Continental S.A. av C.V.
- Tipler, P. (2006) Fysik för vetenskap och teknik. 5: e utgåvan Volym 2. Redaktionellt Reverté.
- Serway, R. Fysik för vetenskap och teknik. Volym 2. 7: e. Ed. Cengage Learning.



Ingen har kommenterat den här artikeln än.