De Pascals princip, eller Pascals lag, fastställer att en förändring av trycket hos en vätska som är innesluten i någon av dess punkter överförs utan förändring till alla andra punkter i vätskan.
Denna princip upptäcktes av den franska forskaren Blaise Pascal (1623 - 1662). På grund av vikten av de bidrag som Pascal har gjort till vetenskapen har tryckenheten i det internationella systemet utsetts till hans ära..
Eftersom trycket definieras som förhållandet mellan kraften vinkelrätt mot en yta och dess yta är 1 Pascal (Pa) lika med 1 newton / mtvå.
Artikelindex
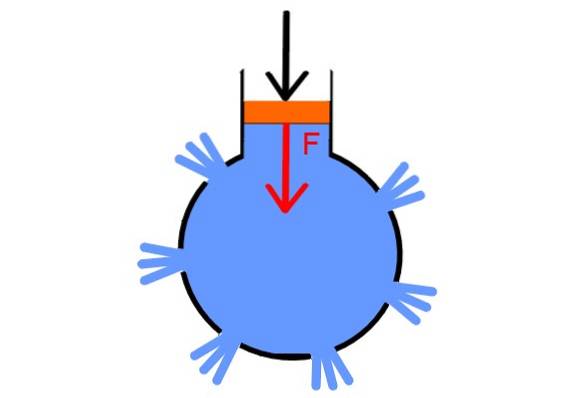
För att testa sin princip tog Pascal fram ett ganska kraftfullt bevis. Han tog en ihålig sfär och borrade på flera ställen, satte in pluggar i alla hål utom en, genom vilken han fyllde den med vatten. I detta placerade han en spruta utrustad med en kolv.
Genom att tillräckligt öka trycket i kolven släpps pluggarna samtidigt, eftersom trycket överförs lika till alla punkter i vätskan och i alla riktningar, vilket visar Pascals lag.
Blaise Pascal hade ett kort liv, präglat av sjukdom. Hans otroliga omfång fick honom att undersöka olika aspekter av naturen och filosofin. Hans bidrag var inte begränsade till att studera vätskornas beteende, Pascal var också en pionjär inom databehandling.
Och det är att Pascal vid 19 års ålder skapade en mekanisk räknare för sin far att använda i sitt arbete i det franska skattesystemet: pascaline.
Tillsammans med sin vän och kollega den stora matematikaren Pierre de Fermat formade de sannolikhetsteorin, oumbärlig inom fysik och statistik. Pascal dog i Paris vid 39 års ålder.
Följande experiment är ganska enkelt: ett U-rör fylls med vatten och pluggar placeras i varje ände som kan glida smidigt och enkelt, som kolvar. Trycket görs mot den vänstra kolven, sjunker den lite och det observeras att den till höger stiger, tryckt av vätskan (figur nedan).
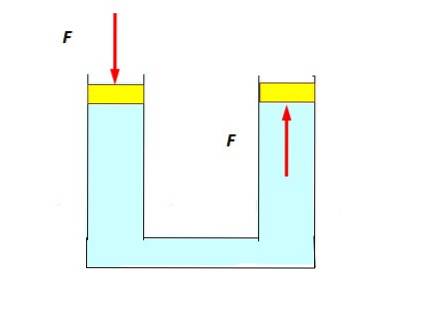
Detta händer eftersom trycket överförs utan någon minskning till alla vätskans punkter, inklusive de som är i kontakt med kolven till höger..
Vätskor som vatten eller olja är komprimerbara men samtidigt har molekylerna tillräcklig rörelsefrihet, vilket gör det möjligt för trycket att fördelas över höger kolv..
Tack vare detta får den högra kolven en kraft som är exakt lika i storlek och riktning som den som appliceras till vänster, men i motsatt riktning..
Trycket i en statisk vätska är oberoende av behållarens form. Det kommer snart att visas att trycket varierar linjärt med djupet och Pascals princip är en följd av detta..
En tryckförändring vid vilken punkt som helst gör att trycket vid en annan punkt ändras med samma mängd. Annars skulle det finnas ett extra tryck som skulle få vätskan att strömma.
En vätska i vila utövar en kraft på behållarens väggar som innehåller den och även på ytan på något föremål som är nedsänkt i den. I Pascals sprutexperiment ser man att vattenstrålarna kommer ut vinkelrätt till sfären.
Vätskorna fördelar kraften vinkelrätt på ytan på vilken den verkar, det är därför det är bekvämt att införa begreppet medeltryck Pm som den vinkelräta kraften utövar F⊥ Efter område TILL, vars SI-enhet är pascal:
Pm = F⊥ / TILL
Trycket ökar med djupet. Det kan ses genom att isolera en liten del vätska i statisk jämvikt och tillämpa Newtons andra lag:
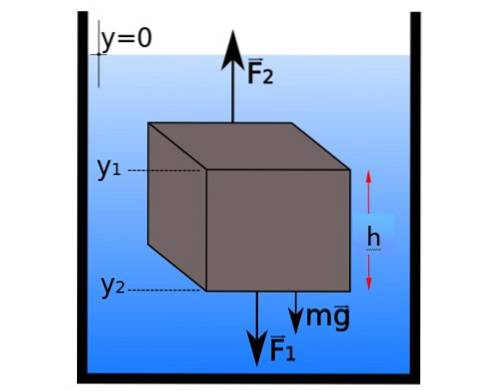
De horisontella krafterna avlägsnas parvis, men i vertikal riktning grupperas krafterna så här:
∑FY = Ftvå - F1 - mg = 0 → Ftvå - F1 = mg
Uttrycker massa i termer av densitet ρ = massa / volym:
Ptvå.A- P1.A = ρ x volym x g
Volymen av vätskedelen är produkten A x h:
A. (Ptvå - P1) = ρ x A x h x g
ΔP = ρ.g.h Grundläggande sats för hydrostatik
Pascals princip har använts för att bygga många enheter som multiplicerar kraften och underlättar uppgifter som att lyfta vikter, stämpla på metall eller pressa föremål. Bland dem är:
-Hydraulpressen
-Bilbromssystemet
-Mekaniska spader och mekaniska armar
-Den hydrauliska domkraften
-Kranar och hissar
Låt oss sedan se hur Pascals princip förvandlar små krafter till stora krafter för att göra alla dessa jobb. Hydraulpressen är det mest karakteristiska exemplet och kommer att analyseras nedan.
För att bygga en hydraulisk press tas samma enhet som bilden ovan, det vill säga en U-formad behållare, av vilken vi redan vet att samma kraft överförs från en kolv till en annan. Skillnaden kommer att vara storleken på kolvarna och det är det som får enheten att fungera.
Följande bild visar Pascals princip i aktion. Trycket är detsamma vid alla punkter i vätskan, både i den lilla och stora kolven:
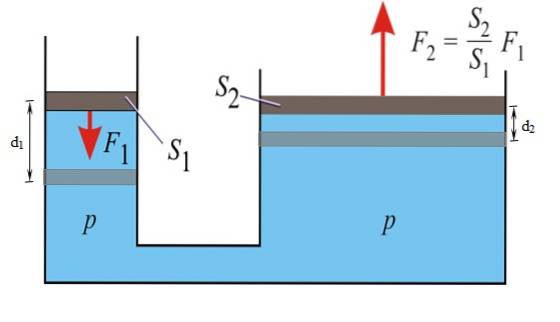
p = F1 / S1 = Ftvå / Stvå
Storleken på kraften som överförs till den stora kolven är:
Ftvå = (Stvå / S1). F1
Gillartvå > S1, resulterar i Ftvå > F1, därför har utgångskraften multiplicerats med faktorn som ges av kvoten mellan områdena.
Detta avsnitt presenterar applikationsexempel.
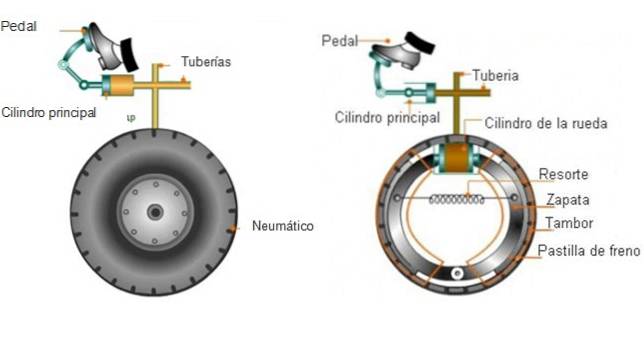
Bilbromsar använder Pascals princip genom en hydraulvätska som fyller rör som är anslutna till hjulen. När han behöver stanna, använder föraren en kraft genom att trycka ner bromspedalen och skapa vätsketryck.
Å andra sidan trycker trycket på bromsbeläggen mot trumman eller bromsskivorna som roterar tillsammans med hjulen (inte däcken). Den resulterande friktionen gör att skivan stannar och bromsar också hjulen.
I hydraulpressen i figuren nedan måste ingångsarbetet vara lika med utgångsarbetet så länge friktion inte beaktas..
Ingångskraft F1 får kolven att färdas ett avstånd d1 går ner, medan uteffekten Ftvå tillåter en rundtur dtvå av den stigande kolven. Om det mekaniska arbetet som utförs av båda krafterna är detsamma:
F1.d1 = Ftvå. dtvå
Den mekaniska fördelen M är kvoten mellan ingångskraftens storlek och utgångskraften:
M = Ftvå/ F1 = d1/ dtvå
Och som visas i föregående avsnitt kan det också uttryckas som kvoten mellan områdena:
Ftvå/ F1 = Stvå / S1
Det verkar som att arbete kan utföras gratis men i själva verket skapas inte energi med denna anordning, eftersom den mekaniska fördelen uppnås på bekostnad av förskjutningen av den lilla kolven d1.
För att optimera prestanda läggs ett ventilsystem till enheten på ett sådant sätt att utloppskolven stiger tack vare korta impulser på inloppskolven..
På detta sätt pumpar operatören av en hydraulisk garagejack flera gånger för att gradvis lyfta ett fordon..
I den hydrauliska pressen i figur 5 är kolvytorna 0,5 kvadrat tum (liten kolv) och 25 kvadrat tum (stor kolv). Hitta:
a) Den mekaniska fördelen med denna press.
b) Kraften som krävs för att lyfta en last på 1 ton.
c) Avståndet som ingångskraften måste verka för att lyfta lasten med 1 tum.
Uttrycka alla resultat i enheter i det brittiska systemet och SI International System.
a) Den mekaniska fördelen är:
M = Ftvå/ F1 = Stvå/ S1 = 25 tumtvå / 0,5 tumtvå = 50
b) 1 ton är lika med 2000 lb-kraft. Kraften som krävs är F1:
F1 = Ftvå / M = 2000 lb-kraft / 50 = 40 lb-kraft
För att uttrycka resultatet i det internationella systemet krävs följande omvandlingsfaktor:
1 lb-kraft = 4448 N
Därför är storleken på F1 177,92 N.
c) M = d1/ d2 → d1 = M.dtvå = 50 x 1 tum = 50 tum
Den nödvändiga omvandlingsfaktorn är: 1 tum = 2,54 cm
d1 = 127 cm = 1,27 m
Ingen har kommenterat den här artikeln än.