
Teoretisk sannolikhet hur man får det, exempel, övningar
De teoretisk sannolikhet (eller Laplace) att en händelse E inträffar som tillhör ett samplingsutrymme S, där alla händelser har samma sannolikhet för händelse, definieras i matematisk notation som: P (E) = n (E) / N (S)
Där P (E) är sannolikheten ges som kvoten mellan det totala antalet möjliga utfall av händelsen E, som vi kallar n (E), dividerat med det totala antalet N (S) av möjliga utfall i provutrymmet S.

Den teoretiska sannolikheten är ett reellt tal mellan 0 och 1, men uttrycks ofta som en procentsats, i vilket fall sannolikheten kommer att vara ett värde mellan 0% och 100%.
Att beräkna sannolikheten för att en händelse inträffar är mycket viktigt inom många områden, såsom handel, försäkringsbolag, spel och många fler..
Artikelindex
- 1 Hur man får den teoretiska sannolikheten?
- 2 Exempel
- 2.1 Exempel 1
- 2.2 Exempel 2
- 3 Övningar
- 3.1 Övning 1
- 3.2 Övning 2
- 3.3 Övning 3
- 3.4 Övning 4
- 4 Referenser
Hur man får den teoretiska sannolikheten?
Ett illustrativt fall är fallet med lotterier eller lotterier. Antag att 1000 biljetter utfärdas för att lotta en smartphone. Eftersom dragningen görs slumpmässigt har alla biljetter lika chans att bli en vinnare.
För att hitta sannolikheten att en person som köper en biljett med nummer 81 är en vinnare, beräknas följande teoretisk sannolikhet:
P (1) = 1/1 000 = 0,001 = 0,1%
Föregående resultat tolkas som följer: om dragningen upprepades oändligt många gånger skulle varje 1000 gånger biljett 81 väljas i genomsnitt en gång.
Om någon av någon anledning köper alla biljetter är det säkert att de vinner priset. Sannolikheten för att vinna priset om du har alla biljetter beräknas enligt följande:
P (1 000) = 1 000/1 000 = 1 = 100%.
Det vill säga att sannolikheten 1 eller 100% betyder att det är helt säkert att detta resultat kommer att uppstå..
Om någon äger 500 biljetter är chansen att vinna eller förlora densamma. Den teoretiska sannolikheten för att vinna priset beräknas i detta fall enligt följande:
P (500) = 500/1000 = ½ = 0,5 = 50%.
Den som inte köper någon biljett har ingen chans att vinna och hans teoretiska sannolikhet bestäms enligt följande:
P (0) = 0/1 000 = 0 = 0%
Exempel
Exempel 1
Du har ett mynt med dyr på ena sidan och skydda eller stämpel på den andra. När myntet kastas, vad är den teoretiska sannolikheten för att det kommer upp på huvudet??
P (dyr) = n (dyr) / N ( ansikte + sköld ) = ½ = 0,5 = 50%
Resultatet tolkas på följande sätt: om ett stort antal kast gjordes skulle i genomsnitt varje 2 kast kastas en av dem.
I procent är tolkningen av resultatet att utföra ett oändligt stort antal kast, i genomsnitt av 100 av dem 50 skulle resultera i huvuden.
Exempel 2
I en låda finns 3 blå kulor, 2 röda kulor och 1 gröna. Vad är den teoretiska sannolikheten att när du tar en marmor ur lådan blir den röd?
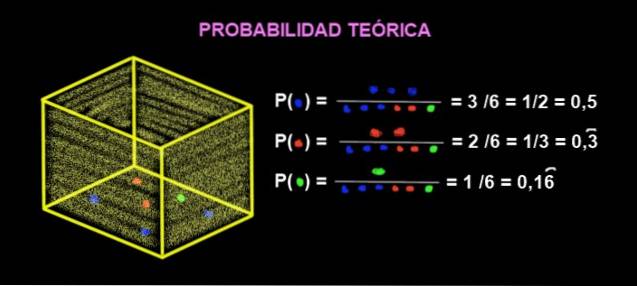
Sannolikheten att den blir röd är:
P (röd) = Antal gynnsamma fall / Antal möjliga fall
Nämligen:
P (röd) = Antal röda kulor / Totalt antal kulor
Slutligen är sannolikheten att en röd marmor dras:
P (röd) = 2/6 = ⅓ = 0,33333 = 33,33%
Medan sannolikheten att när man ritar en grön marmor är:
P (grön) = ⅙ = 0,1666 = 16,66%
Slutligen är den teoretiska sannolikheten för att få en blå marmor i en blind extraktion:
P (blå) = 3/6 = ½ = 0,5 = 50%
Det vill säga, för vartannat försök blir resultatet blått i en av dem och en annan färg i ett nytt försök, under förutsättningen att den extraherade marmorn ersätts och att antalet försök är mycket, mycket stort..
Träning
Övning 1
Bestäm sannolikheten för att vid val av en matris erhålls ett värde som är mindre än eller lika med 4.
Lösning
För att beräkna sannolikheten för att denna händelse inträffar kommer definitionen av teoretisk sannolikhet att tillämpas:
P (≤4) = Antal gynnsamma fall / Antal möjliga fall
P (≤5) = 5/6 = = 83,33%
Övning 2
Hitta sannolikheten att vid två kast i rad av en normal sexsidig matris kommer 5 att rulla två gånger.
Lösning
För att svara på denna övning är det bekvämt att skapa en tabell för att visa alla möjligheter. Den första siffran indikerar resultatet av den första formen och den andra resultatet av den andra.
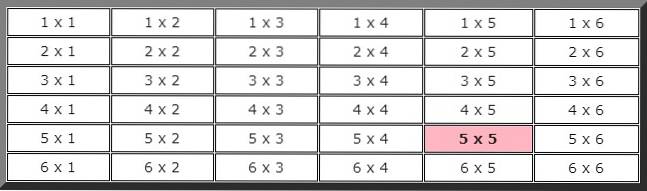
För att beräkna den teoretiska sannolikheten behöver vi veta det totala antalet möjliga fall, i det här fallet, som framgår av föregående tabell, finns det 36 möjligheter.
Även iakttagande av tabellen kan man dra slutsatsen att antalet fall som är gynnsamma för händelsen att i de två på varandra följande lanseringarna 5 är endast 1, markerat med färg, därför är sannolikheten att denna händelse inträffar:
P (5 x 5) = 1/36.
Detta resultat kunde också ha uppnåtts med en av egenskaperna för teoretisk sannolikhet, som anger att den kombinerade sannolikheten för två oberoende händelser är produkten av deras individuella sannolikheter..
I det här fallet är sannolikheten att det första kastet kommer att rulla 5 är ⅙. Det andra kastet är helt oberoende av det första, därför är sannolikheten att 5 rullas i det andra också ⅙. Så den kombinerade sannolikheten är:
P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.
Övning 3
Hitta sannolikheten att ett nummer mindre än 2 rullas vid det första kastet och ett nummer större än 2 rullas på det andra.
Lösning

Återigen måste en tabell över möjliga händelser byggas, där de där det första kastet var mindre än 2 och i det andra större än 2 markeras..
Totalt finns det 4 möjligheter av totalt 36. Det vill säga sannolikheten för denna händelse är:
P (<2 ; >2) = 4/36 = 1/9 = 0.1111 = 11.11%
Med hjälp av sannolikhetssatsen som säger:
Sannolikheten att två oberoende händelser inträffar är lika med produkten av de enskilda sannolikheterna.
Samma resultat erhålls:
P (<2) P(>2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%
Värdet som erhålls med denna procedur sammanfaller med föregående resultat genom den teoretiska eller klassiska definitionen av sannolikhet.
Övning 4
Vad är sannolikheten att när du kastar två tärningar är summan av värdena 7.
Lösning

För att hitta lösningen i det här fallet har en tabell över möjligheter upprättats där de fall som uppfyller villkoret att summan av värdena är 7 har indikerats i färg.
Om man tittar på tabellen kan 6 möjliga fall räknas, så sannolikheten är:
P (I + II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%
Referenser
- Canavos, G. 1988. Sannolikhet och statistik: Tillämpningar och metoder. Mcgraw hill.
- Devore, J. 2012. Sannolikhet och statistik för teknik och vetenskap. 8: e. Utgåva. Cengage.
- Lipschutz, S. 1991. Schaum-serien: Sannolikhet. Mcgraw hill.
- Obregón, I. 1989. Teori om sannolikhet. Ledare Limusa.
- Walpole, R. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.


Ingen har kommenterat den här artikeln än.