
Polytropiska processegenskaper, applikationer och exempel
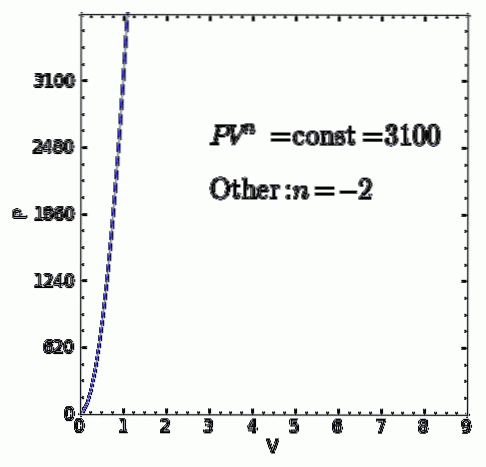
A polytropisk process är en termodynamisk process som inträffar när förhållandet mellan trycket P och volymen V getts av P.Vn det förblir konstant. Exponenten n är ett reellt tal, vanligtvis mellan noll och oändlighet, men i vissa fall kan det vara negativt.
Värdet av n får namnet på polytropiindex och det är viktigt att markera att under en polytrop termodynamisk process måste nämnda index bibehålla ett fast värde, annars kommer processen inte att betraktas som polytropisk.

Artikelindex
- 1 Kännetecken för polytropa processer
- 2 applikationer
- 2.1 Arbeta med polytropiska processer för olika värden på n
- 3 Exempel på polytropa processer
- 3.1 - Exempel 1
- 3.2 - Exempel 2
- 4 Referenser
Kännetecken för polytropa processer
Några karakteristiska fall av polytropa processer är:
- Den isotermiska processen (vid konstant temperatur T), där exponenten är n = 1.
- En isobar process (vid konstant tryck P), i detta fall n = 0.
- Den isokoriska processen (vid konstant volym V), för vilken n = + ∞.
- Adiabatiska processer (vid konstant S-entropi), där exponenten är n = γ, där γ är den adiabatiska konstanten. Denna konstant är kvoten mellan värmekapaciteten vid konstant tryck Cp dividerat med värmekapaciteten vid konstant volym Cv:
y = Cp / Cv
- Varje annan termodynamisk process som inte är en av de tidigare fallen. men det överensstämmer P.Vn = ctte med verkligt och konstant polytropiskt index n det kommer också att vara en polytropisk process.
Applikationer
En av de huvudsakliga tillämpningarna av den polytropiska ekvationen är att beräkna det arbete som utförs av ett slutet termodynamiskt system, när det passerar från ett initialtillstånd till ett slutligt tillstånd på ett kvasistatiskt sätt, det vill säga efter en följd av jämviktstillstånd.
Arbeta med polytropiska processer för olika värden på n
För n ≠ 1
Det mekaniska arbetet W utfört av ett slutet termodynamiskt system beräknas med uttrycket:
W = ∫P.dV
Där P är trycket och V volymen.
Som i fallet med en polytropisk process är förhållandet mellan tryck och volym:
P.V n = konstant = C
Lösa för P från föregående uttryck för att ersätta det i arbetsuttrycket:
P = C /V n
Vi har det mekaniska arbetet som utförs under en polytropisk process, som börjar i ett initialt tillstånd 1 och slutar i det slutliga tillståndet 2. Allt detta visas i följande uttryck:


C = P1 V1n = Ptvå Vtvån
Genom att ersätta konstantens värde i arbetsuttrycket får vi:
W = (Ptvå Vtvå - P1 V1) / (1-n)
Om det arbetande ämnet kan modelleras som en idealgas, har vi följande tillståndsekvation:
P.V = m.R.T
Där m är antalet mol av den ideala gasen och R är den universella gaskonstanten.
För en idealisk gas som följer en polytropisk process med ett polytropiindex som skiljer sig från enhet och som passerar från ett tillstånd med initialtemperatur T1 till ett annat tillstånd med temperatur Ttvå vi har att det utförda arbetet ges med följande formel:
W = mR (Ttvå - T1) / (1-n)
För n → ∞
Enligt formeln för arbetet som erhölls i föregående avsnitt har vi att arbetet med en polytropisk process med n = ∞ är noll, eftersom uttrycket för arbetet divideras med oändlighet och därför tenderar resultatet att vara noll.
Ett annat sätt att nå detta resultat är från förhållandet P1 V1n = Ptvå Vtvån, som kan skrivas om på följande sätt:
(S1/ Ptvå) = (V.två/ V1)n
Med den nionde roten i varje medlem får vi:
(Vtvå/ V1) = (P1/ Ptvå)(1 / n)
Om n → ∞ har vi (Vtvå/ V1) = 1, vilket betyder att:
Vtvå = V1
Det vill säga volymen ändras inte i en polytropisk process med n → ∞. Därför är volymskillnaden dV i integralen av mekaniskt arbete 0. Dessa typer av polytropa processer är också kända som processer isokorisk, eller processer med konstant volym.
För n = 1
Återigen har vi uttrycket uttryck för arbete:
W = ∫P dV
När det gäller en polytropisk process med n = 1 är förhållandet mellan tryck och volym:
P V = konstant = C
Genom att lösa P från det föregående uttrycket och ersätta har vi arbetet gjort för att gå från initialtillstånd 1 till slutligt tillstånd 2:

Nämligen:
W = C ln (Vtvå/ V1).
Eftersom de initiala och slutliga tillstånden är väl bestämda, kommer också ctte att göra det. Nämligen:
C = P1 V1 = Ptvå Vtvå
Slutligen har vi följande användbara uttryck för att hitta det mekaniska arbetet i ett polytropiskt slutet system där n = 1.
W = P1 V1 ln (Vtvå/ V1) = Ptvå Vtvå ln (Vtvå/ V1)
Om arbetsämnet består av m mol idealgas, då kan den ideala gasekvationen av tillstånd tillämpas: P V = m.R.T.
I detta fall, som P.V1 = ctte, vi har att en polytropisk process med n = 1 är en process vid konstant temperatur T (isotermisk), så att följande uttryck för arbetet kan erhållas:
W = m R T1 ln (Vtvå/ V1) = m R Ttvå ln (Vtvå/ V1)

Exempel på polytropa processer
- Exempel 1
Anta att en cylinder med en rörlig kolv fylld med ett kilo luft. Ursprungligen upptar luften en volym V.1= 0,2 m3 vid ett tryck P1= 400 kPa. En polytropisk process följs med n = γ = 1,4, vars slutliga tillstånd har tryck Ptvå = 100 kPa. Bestäm det arbete som utförs av luften på kolven.
Lösning
När polytropiindex är lika med den adiabatiska konstanten, finns det en process där arbetssubstansen (luften) inte utbyter värme med miljön och därför förändras inte entropin..
För luft, en diatomisk idealgas, har vi:
y = Cp / Cv, med Cp = (7/2) R och Cv = (5/2) R
Sedan:
y = 7/5 = 1,4
Med hjälp av uttrycket för den polytropiska processen kan den slutliga volymen av luften bestämmas:
Vtvå = [(Ptvå V11.4) / Ptvå](1 / 1.4) = 0,54 m3.
Nu har vi villkoren för att tillämpa formeln för arbete som utförts i en polytropisk process för n ≠ 1 erhållen ovan:
W = (Ptvå Vtvå - P1 V1) / (1-n)
Att ersätta lämpliga värden som vi har:
W = (100 kPa 0,54 m3 - 400 kPa 0,2 m3) / (1 - 1,4) = 65,4 kJ
- Exempel 2
Anta samma cylinder från exempel 1 med en rörlig kolv fylld med ett kilo luft. Ursprungligen upptar luften en volym V1 = 0,2 m3 vid ett tryck P1 = 400 kPa. Men till skillnad från föregående fall expanderar luften isotermiskt för att nå ett slutligt tryck P2 = 100 kPa. Bestäm det arbete som utförs av luften på kolven.
Lösning
Som tidigare ses är isotermiska processer polytropa processer med index n = 1, så det är sant att:
P1 V1 = P2 V2
På detta sätt kan den slutliga volymen lätt skalas av för att erhålla:
V2 = 0,8 m3
Sedan använder vi det arbetsuttryck som erhållits tidigare för fallet n = 1, att arbetet som utförs av luften på kolven i denna process är:
W = P1 V1 ln (V2 / V1) = 400000 Pa × 0,2 m3 ln (0,8 / 0,2) = 110,9 kJ.
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill.
- Cengel, Y. 2012. Termodynamik. 7: e upplagan. Mcgraw hill.
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 4. Vätskor och termodynamik. Redigerad av Douglas Figueroa (USB).
- López, C. Den första lagen om termodynamik. Återställd från: culturacientifica.com.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9: e upplagan Cengage Learning.
- Sevilla universitet. Termiska maskiner. Återställd från: laplace.us.es.
- Wikiwand. Polytropisk process. Återställd från: wikiwand.com.



Ingen har kommenterat den här artikeln än.