De egenskaper av jämlikhet hänvisa till förhållandet mellan två matematiska objekt, oavsett om det är tal eller variabler. Det betecknas med symbolen "=", som alltid går mitt i dessa två objekt. Detta uttryck används för att fastställa att två matematiska objekt representerar samma objekt; i ett annat ord, att två objekt är samma sak.
Det finns fall där det är trivialt att använda jämlikhet. Det är till exempel klart att 2 = 2. Men när det gäller variabler är det inte längre trivialt och har specifika användningsområden. Om vi till exempel har det y = x och å andra sidan x = 7 kan vi dra slutsatsen att y = 7 också.
Ovanstående exempel är baserat på en av egenskaperna för jämlikhet, som du kommer att se inom kort. Dessa egenskaper är väsentliga för att lösa ekvationer (jämlikheter med variabler), som utgör en mycket viktig del i matematik..
Artikelindex
Den reflexiva egenskapen, i fallet med jämställdhet, säger att varje tal är lika med sig själv och uttrycks som b = b för alla reella tal b.
I det särskilda fallet med jämlikhet verkar denna egenskap vara uppenbar, men i andra typer av förhållanden mellan siffror är det inte. Med andra ord uppfyller inte varje verkligt talförhållande denna egenskap. Till exempel kan ett sådant fall av förhållandet "mindre än" (<); ningún número es menor que sí mismo.
Den symmetriska egenskapen för jämställdhet säger att om a = b, då b = a. Det spelar ingen roll vilken ordning som används i variablerna, den kommer att bevaras av jämställdhetsrelationen.
En viss analogi av denna egenskap med kommutativ egenskap kan observeras vid tillägg. Till exempel, på grund av den här egenskapen motsvarar det att skriva y = 4 eller 4 = y.
Den transitiva egenskapen på jämställdhet säger att om a = b och b = c, då a = c. Till exempel 2 + 7 = 9 och 9 = 6 + 3; därför har vi den transitiva egenskapen att 2 + 7 = 6 + 3.
En enkel applikation är följande: antag att Julian är 14 år och att Mario är i samma ålder som Rosa. Om Rosa är i samma ålder som Julian, hur gammal är Mario?
Bakom detta scenario används den transitiva egenskapen två gånger. Matematiskt tolkas det så här: låt “a” vara Marions ålder, “b” Rosa ålder och “c” Julians ålder. Det är känt att b = c och att c = 14.
Genom den transitiva egenskapen har vi att b = 14; det vill säga Rosa är 14 år gammal. Eftersom a = b och b = 14, med den transitiva egenskapen igen har vi att a = 14; det vill säga Marios ålder är också 14 år gammal.
Den enhetliga egenskapen är att om båda sidor av en jämlikhet läggs till eller multipliceras med samma belopp, är jämlikheten bevarad. Till exempel, om 2 = 2, då 2 + 3 = 2 + 3, vilket är klart, eftersom 5 = 5. Den här egenskapen är mest användbar när man försöker lösa en ekvation.
Antag till exempel att du blir ombedd att lösa ekvationen x-2 = 1. Det är bekvämt att komma ihåg att lösningen av en ekvation består i att uttryckligen bestämma variabeln (eller variablerna) som är inblandade, baserat på ett specifikt tal eller en tidigare specificerad variabel..
Att gå tillbaka till ekvationen x-2 = 1, vad du behöver göra är att hitta exakt hur mycket x är värd. För detta måste variabeln rensas.
Det har felaktigt lärts ut att i det här fallet, eftersom siffran 2 är negativ, går den till den andra sidan av jämställdheten med ett positivt tecken. Men det är inte korrekt att säga det på det sättet.
I grund och botten är det du gör att tillämpa den enhetliga egenskapen, som vi kommer att se nedan. Tanken är att rensa "x"; det vill säga, lämna det ensamt på ena sidan av ekvationen. Enligt konvention lämnas det vanligtvis på vänster sida.
För detta ändamål är antalet att "eliminera" -2. Sättet att göra det skulle vara genom att lägga till 2, eftersom -2 + 2 = 0 och x + 0 = 0. För att kunna göra detta utan att ändra jämställdheten måste samma operation tillämpas på den andra sidan.
Detta gör det möjligt att förverkliga den enhetliga egenskapen: eftersom x-2 = 1, om siffran 2 läggs till på båda sidor av jämställdheten, säger den enhetliga egenskapen att den inte ändras. Sedan har vi det x-2 + 2 = 1 + 2, vilket motsvarar att säga att x = 3. Med detta skulle ekvationen lösas.
På samma sätt, om du vill lösa ekvationen (1/5) y-1 = 9, kan du fortsätta med den enhetliga egenskapen enligt följande:
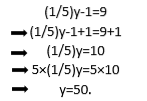
Mer allmänt kan följande uttalanden göras:
- Om a-b = c-b, då a = c.
- Om x-b = y är x = y + b.
- Om (1 / a) z = b är z = a ×
- Om (1 / c) a = (1 / c) b, då a = b.
Annulleringsegenskapen är ett särskilt fall av den enhetliga egenskapen, särskilt med tanke på subtraktion och delning (som i grunden också motsvarar addition och multiplikation). Den här egenskapen behandlar detta fall separat.
Till exempel, om 7 + 2 = 9, då 7 = 9-2. Eller om 2y = 6, då y = 3 (dividerat med två på båda sidor).
Analogt med det föregående fallet, genom annulleringsegenskapen, kan följande uttalanden fastställas:
- Om a + b = c + b, då a = c.
- Om x + b = y är x = y-b.
- Om az = b är z = b / a.
- Om ca = cb, då a = b.
Om vi känner till värdet av ett matematiskt objekt anger substitutionsegenskapen att detta värde kan ersättas i valfri ekvation eller uttryck. Till exempel, om b = 5 och a = bx, då ersätter du värdet av "b" i den andra likheten har vi att a = 5x.
Ett annat exempel är följande: om "m" delar "n" och även "n" delar "m", måste det ha att m = n.
Att säga att "m" delar "n" (eller motsvarande att "m" är en delare av "n") betyder faktiskt att delningen m ÷ n är exakt; att dela "m" med "n" ger ett heltal, inte ett decimal. Detta kan uttryckas genom att säga att det finns ett heltal "k" så att m = k × n.
Eftersom "n" också delar "m", finns det ett heltal "p" så att n = p × m. På grund av substitutionsegenskapen har vi att n = p × k × n, och för att detta ska hända finns det två möjligheter: n = 0, i vilket fall vi skulle ha identiteten 0 = 0; eller p × k = 1, därav identiteten n = n.
Antag att "n" inte är noll. Då nödvändigtvis p × k = 1; därför är p = 1 och k = 1. Genom att använda substitutionsegenskapen igen, när vi ersätter k = 1 i likheten m = k × n (eller motsvarande, p = 1 i n = p × m) får vi äntligen att m = n, vilket var vad vi ville visa.
Precis som tidigare sågs att om en operation som tillägg, multiplikation, subtraktion eller delning görs i båda termerna av en jämlikhet, bevaras den, på samma sätt kan andra operationer som inte förändrar en jämlikhet tillämpas.
Nyckeln är att alltid utföra den på båda sidor av jämställdheten och i förväg se till att operationen kan utföras. Så är fallet med empowerment; det vill säga om båda sidor av en ekvation höjs till samma kraft har vi fortfarande en jämlikhet.
Till exempel, eftersom 3 = 3, så 3två= 3två (9 = 9). I allmänhet ges ett heltal "n", om x = y, då xn= ochn.
Detta är ett särskilt fall av empowerment och tillämpas när makten är ett icke-heltal rationellt tal, såsom ½, som representerar kvadratroten. Denna egenskap anger att om samma rot tillämpas på båda sidor av en jämlikhet (när det är möjligt), är jämlikheten bevarad.
Till skillnad från föregående fall måste man vara försiktig med pariteten hos roten som ska tillämpas, eftersom det är välkänt att den jämna roten till ett negativt tal inte är väl definierat.
Om radikalen är jämn, finns det inga problem. Till exempel om x3= -8, även om det är en jämlikhet, kan du till exempel inte tillämpa en kvadratrot på båda sidor. Men om du kan tillämpa en kubrot (vilket är ännu bekvämare om du vill veta värdet på x uttryckligen) och därmed få det x = -2.
Ingen har kommenterat den här artikeln än.