Vad är skjuvmodulen, styvhet eller skjuvning? (Övningar lösta)

De skärmodul beskriver svaret från ett material på appliceringen av en skjuvspänning som deformerar det. Andra ofta använda namn för skjuvmodul är skjuvmodul, skjuvmodul, tvärelasticitet eller tangentiell elasticitet..

När spänningarna är små är deformationerna proportionella mot dem, enligt Hookes lag, där skjuvmodulen är proportionalitetskonstanten. Därför:

Skjuvmodul = Skjuvspänning / töjning

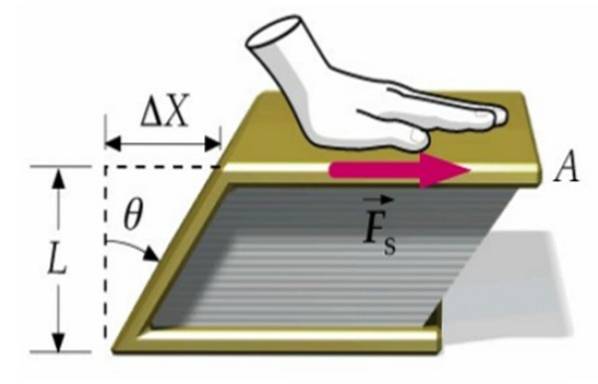
Antag att den ena kraften appliceras på omslaget till en bok, den andra är fixerad på bordets yta. På det här sättet rör sig boken som helhet inte utan deformeras när det övre omslaget rör sig i förhållande till det nedre. Δx.

Boken går från att ha ett rektangulärt tvärsnitt till ett parallellogramformat avsnitt, som vi ser på bilden ovan.

Vara:

τ = F / A

Skjuvspänningen eller spänningen, varelsen F storleken på den applicerade kraften och TILL det område som den agerar på.

Deformationen orsakad ges av kvoten:

δ = Ax / L

Därför är skjuvmodulen, som vi kommer att beteckna som G,:

Och eftersom Δx / L inte har några dimensioner är enheterna i G samma som skjuvspänningen, vilket är förhållandet mellan kraft och area..

I det internationella systemet för enheter är dessa enheter Newton / kvadratmeter eller pascal, förkortat Pa. Och i angelsaxiska enheter är det pund / kvadrat tum, förkortat psi.

Artikelindex

• 1 Skärmodul för olika material
  • 1.1 Experimentell mätning av skjuvmodul
  • 1.2 Hur man hittar G?
• 2 Övningar med lösning
  • 2.1 - Övning 1
  • 2.2 - Övning 2
• 3 Referenser

Skärmodul för olika material

Under påverkan av skjuvkrafter som de som beskrivs erbjuder föremålen ett motstånd som liknar bokens, där de inre skikten glider. Denna typ av deformation kan endast förekomma i fasta kroppar, som har tillräcklig styvhet för att motstå deformation..

Å andra sidan erbjuder vätskor inte denna typ av motstånd, men de kan genomgå volymdeformationer.

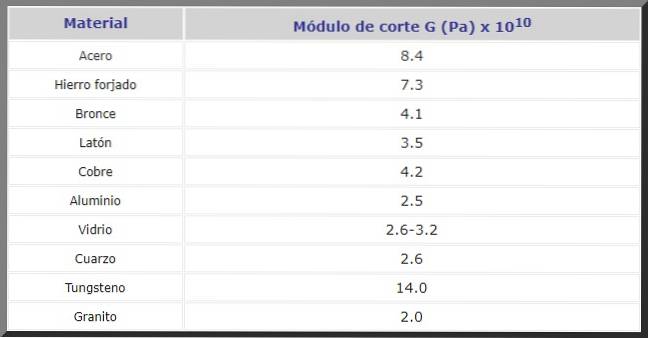
Nedan följer skärmodulen G in Pa för olika material som ofta används vid konstruktion och tillverkning av maskiner och reservdelar av alla slag:

Experimentell mätning av skjuvmodul

För att hitta värdet på skjuvmodulen måste prover av varje material testas och deras svar på appliceringen av en skjuvspänning undersökas..

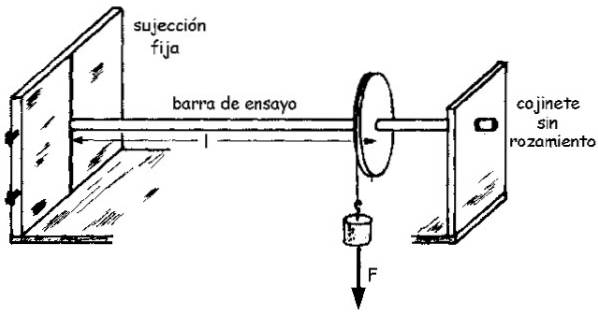
Provet är en stav gjord av materialet med radie R och längd L känd, vilken är fixerad i ena änden, medan den andra är ansluten till axeln på en remskiva som är fri att rotera.

Remskivan är bunden med ett rep i vars fria ände en vikt hängs som utövar en kraft F på stången genom repet. Och den här kraften producerar i sin tur ett ögonblick M på stången, som sedan roterar en liten vinkel θ.

Ett diagram över monteringen kan ses i följande bild:

Momentets storlek M, som vi betecknar som M (ingen fetstil) är relaterad till den roterade vinkeln θ genom skjuvmodulen G enligt följande ekvation (härledd med en enkel integral):

Eftersom momentets storlek är lika med produkten från modulen av kraften F och radien på remskivan R_sid:

M = F.R_sid

Och styrka är vikten som hänger W, sedan:

M = W.R_sid

Byt ut i ekvationen för momentets storlek:

Det finns sambandet mellan vikt och vinkel:

Hur man hittar G?

Detta förhållande mellan variablerna W Y θ är linjär, så de olika vinklarna som produceras genom att hänga olika vikter mäts.

Vikt- och vinkelparet plottas på grafpapper, den bästa linjen som passerar genom de experimentella punkterna monteras och lutningen beräknas. m av nämnda linje.

Övningar med lösning

- Övning 1

En stång 2,5 meter lång och radien 4,5 mm är fixerad i ena änden. Den andra är ansluten till en radiehjul på 75 cm som har en hängande vikt W på 1,3 kg. Den roterade vinkeln är 9,5º.

Med dessa data begärs att beräkna stångens skjuvningsmodul G.

Lösning

Från ekvationen:

G rensas:

Och värdena i uttalandet ersätts, var noga med att uttrycka all data i det internationella systemet för enheter SI:

R = 4,5 mm = 4,5 x 10 ^-3 m

R_sid = 75 cm = 0,075

Att gå från kilogram (som faktiskt är kilo - kraft) till newton multiplicera med 9,8:

W = 1,3 kg-kraft = 1,3 x 9,8 N = 12,74 N.

Och slutligen måste graderna vara i radianer:

9,5 º = 9,5 x2π / 360 radianer = 0,1665 radianer.

Med allt detta har du:

= 2237 x 10¹⁰ Pa

- Övning 2

En kub av gel har en sida på 30 cm. En av dess ansikten är fast, men samtidigt appliceras en parallell kraft på 1 N på motsatt yta, som tack vare den rör sig 1 cm (se exemplet på boken i figur 1).

Det beräknas beräkna med dessa data:

a) Skjuvspänningens storlek

b) Stam δ

c) Värdet på skjuvmodulen

Lösning till

Skjuvspänningen är:

τ = F / A

Med:

A = sida^två = (30 x 10^-två centimeter)^två = 0,09 m^två

Därför:

τ = 1 N / 0,09 m^två = 11,1 Pa

Lösning b

Stam är ingen annan än värdet på δ, ges av:

δ = Ax / L

Förskjutningen av ansiktet som utsätts för kraften är 1 cm, sedan:

5 = 1/30 = 0,0333

Lösning c

Skjuvningsmodulen är kvoten mellan skjuvspänningen och töjningen:

G = Skjuvspänning / töjning

Därför:

G = 11,1 Pa / 0,033 = 336,4 Pa

Referenser

1. Beer, F. 2010. Mekanik av material. McGraw Hill. 5: e. Utgåva.
2. Franco García, A. Solid Rigid. Mätning av skjuvmodul. Återställd från: sc.ehu.es.
3. Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
4. Resnick, R. (1999). Fysisk. Vol. 1. 3: e upplagan på spanska. Compañía Editorial Continental S.A. av C.V.
5. Valladolid universitet. Institutionen för fysik för kondenserad materia. Val av problem. Återställd från: www4.uva.es.