Vad är vektorkvantitet? (Med exempel)

Det definierar vektorkvantitet, eller vektor, såsom den för vilken det är nödvändigt att specificera både dess storlek eller modul (med respektive enheter) och dess riktning.

Till skillnad från vektormängden har en skalär kvantitet bara storlek (och enheter), men ingen riktning. Några exempel på skalära kvantiteter är bland annat temperatur, objektets längd, längd, massa och tid..

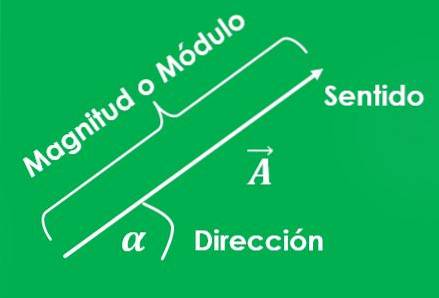
Skillnad mellan vektorkvantitet och skalär

I följande exempel kan du lära dig att skilja en skalär kvantitet från en vektorkvantitet:

En hastighet på 10 km / h är en skalär kvantitet, medan en hastighet på 10 km / h norr är en vektormängd. Skillnaden är att i det andra fallet anges en riktning utöver storleken.

Vektorkvantiteter har ett oändligt antal applikationer, särskilt i fysikens värld.

Grafer och beteckningar av en vektormängd

Sättet att beteckna en vektorkvantitet är att placera en pil (→) på bokstaven som ska användas, eller genom att skriva bokstaven i fetstil (till).

För att rita en vektorkvantitet behöver du ett referenssystem. I det här fallet kommer det kartesiska planet att användas som referenssystem.

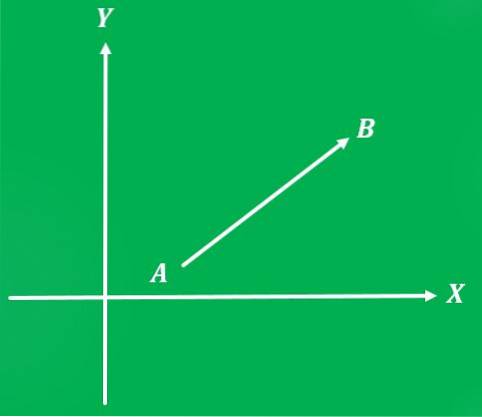
Grafen för en vektor är en linje vars längd representerar storleken; och vinkeln mellan nämnda linje och X-axeln, mätt moturs, representerar dess riktning.

Du måste ange vilken som är startpunkten för vektorn och vilken som är ankomstpunkten. En pil placeras också i slutet av linjen som pekar mot ankomstpunkten, vilket indikerar vektorn.

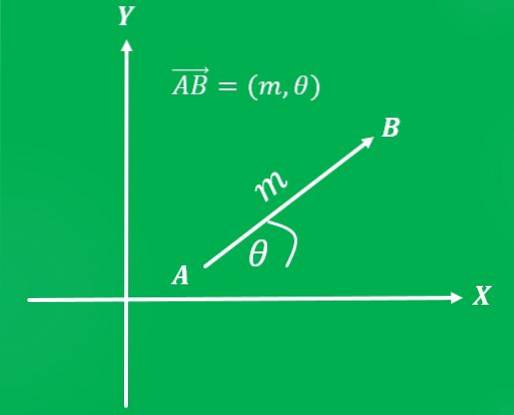
När ett referenssystem har fixats kan vektorn skrivas som ett ordnat par: den första koordinaten representerar dess storlek och den andra koordinaten dess riktning..

Exempel

1- Gravitation som verkar på ett objekt

Om ett föremål placeras på en höjd av 2 meter över marken och det släpps, verkar tyngdkraften på det med en styrka av 9,8 m / s² och en riktning vinkelrät mot marken i en nedåtgående riktning.

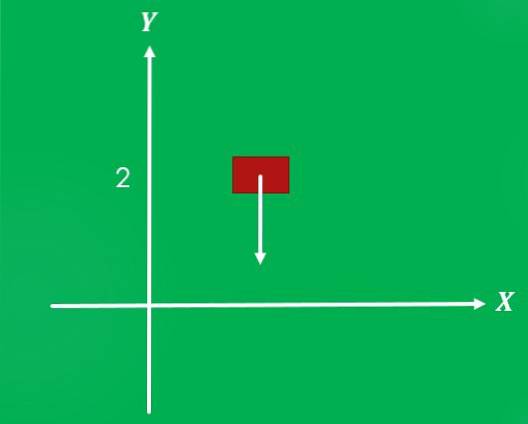
2- Rörelse av ett flygplan

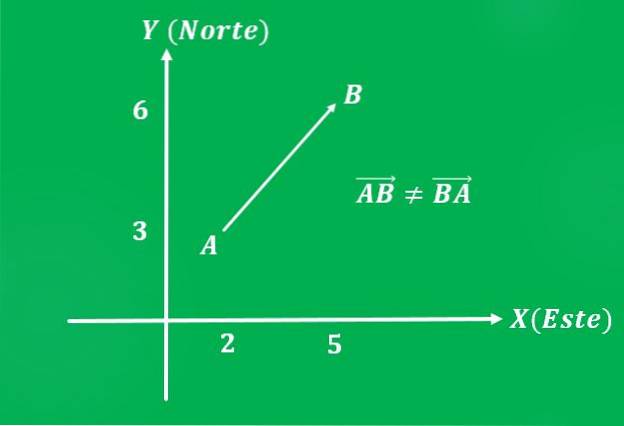
Ett flygplan som reste från punkt A = (2,3) till punkt B = (5,6) på det kartesiska planet, med en hastighet på 650 km / h (magnitude). Banans riktning är 45º nordost (riktning).

Det bör noteras att, om ordningen på punkterna är omvänd, har vektorn samma storlek och samma riktning, men en annan känsla, som kommer att vara sydväst.

3- Kraft tillämpas på ett objekt

Juan bestämmer sig för att skjuta en stol med en kraft på 10 pund, i en riktning parallellt med marken. De möjliga riktningarna för den applicerade kraften är: till vänster eller till höger (när det gäller det kartesiska planet).

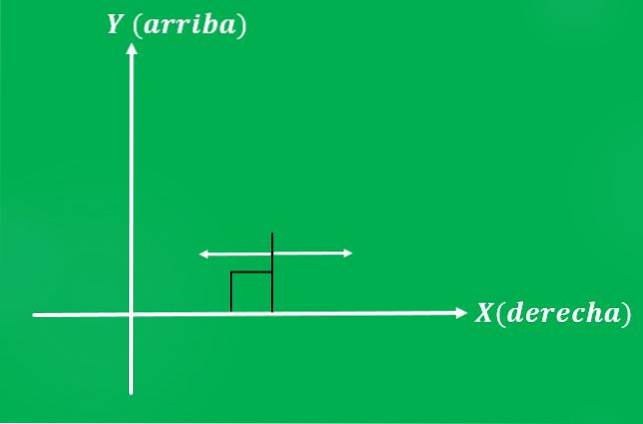
Som i föregående exempel kommer känslan att Juan bestämmer sig för att ge kraften att ge ett annat resultat.

Detta säger oss att två vektorer kan ha samma storlek och riktning, men vara olika (de ger olika resultat).

Två eller flera vektorer kan läggas till och subtraheras, för vilka det finns mycket användbara resultat, såsom Parallelogram-lagen. Du kan också multiplicera en vektor med en skalär.

Referenser

1. Barragan, A., Cerpa, G., Rodríguez, M., & Núñez, H. (2006). Fysik för gymnasiefilmer. Pearson Education.
2. Ford, K. W. (2016). Grundläggande fysik: lösningar på övningarna. World Scientific Publishing Company.
3. Giancoli, D. C. (2006). Fysik: Principer med tillämpningar. Pearson Education.
4. Gómez, A. L. och Trejo, H. N. (2006). Fysik l, ett konstruktivistiskt tillvägagångssätt. Pearson Education.
5. Serway, R. A., & Faughn, J. S. (2001). Fysisk. Pearson Education.
6. Stroud, K. A., & Booth, D. J. (2005). Vektoranalys (Illustrerad utgåva). Industrial Press Inc..
7. Wilson, J. D., & Buffa, A. J. (2003). Fysisk. Pearson Education.