Vad är linjär hastighet? (Med övningar lösta)

De linjär hastighet det definieras som det som alltid är tangentiellt för banan följt av partikeln, oavsett dess form. Om partikeln alltid rör sig i en rätlinjig väg är det inget problem att föreställa sig hur hastighetsvektorn följer denna raka linje.

I allmänhet utförs dock rörelsen på en godtyckligt formad kurva. Varje del av kurvan kan modelleras som om den vore en del av en cirkel med radie till, som vid varje punkt är tangent till den följda vägen.

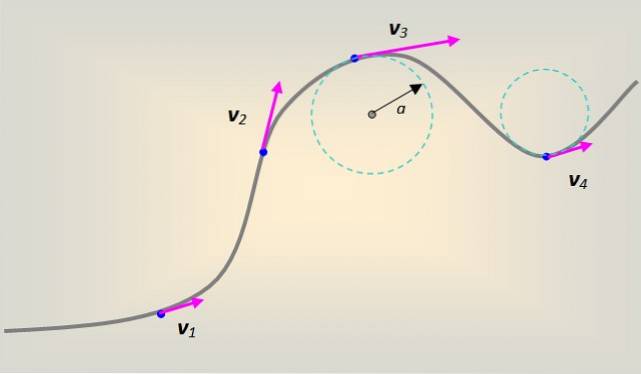
I detta fall följer linjärhastigheten kurvan tangentiellt och hela tiden vid varje punkt i den..

Matematiskt är den momentana linjära hastigheten härledda från positionen i förhållande till tiden. Vara r partikelns positionsvektor vid ett ögonblick t, sedan ges linjär hastighet genom uttrycket:

v = r'(t) = dr / dt

Detta innebär att linjär hastighet eller tangentiell hastighet, som det också ofta kallas, inte är något annat än lägesförändringen med avseende på tiden..

Artikelindex

• 1 Linjär hastighet i cirkelrörelse
  • 1.1 Linjär hastighet, vinkelhastighet och centripetalacceleration
  • 1.2 -Löst övning 1 
  • 1.3 -Löst övning 2
• 2 Referenser

Linjär hastighet i cirkulär rörelse

När rörelsen är på en omkrets kan vi gå bredvid partikeln vid varje punkt och se vad som händer i två mycket speciella riktningar: en av dem är den som alltid pekar mot centrum. Det här är adressen radiell.

Den andra viktiga riktningen är den som passerar omkretsen, detta är riktningen tangentiell och linjär hastighet har det alltid.

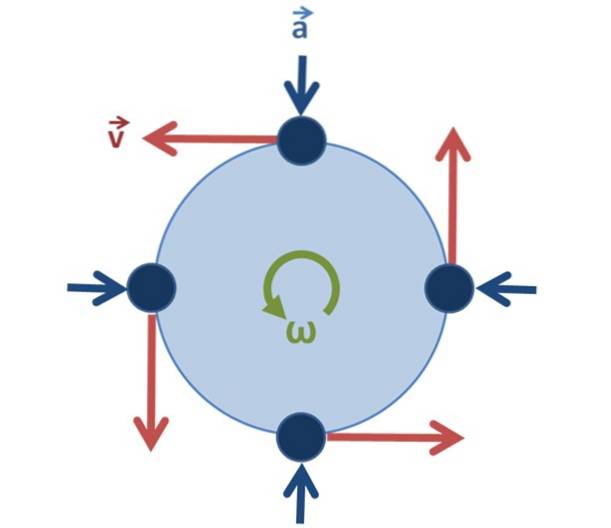
Vid likformig cirkulär rörelse är det viktigt att inse att hastigheten inte är konstant, eftersom vektorn ändrar sin riktning när partikeln roterar, men dess modul (storleken på vektorn), vilket är hastigheten, ja förblir oförändrad.

För denna rörelse ges positionen som en funktion av tiden s (t), var s Är han bågkörning Y t Det är dags. I så fall ges den momentana hastigheten av uttrycket v = ds / dt och det är konstant.

Om hastighetens storlek också varierar (vi vet redan att riktningen alltid gör, annars kunde mobilen inte svänga) står vi inför en varierad cirkelrörelse, under vilken mobilen, förutom att vrida, kan bromsa eller accelerera.

Linjär hastighet, vinkelhastighet och centripetal acceleration

Partikelns rörelse kan också ses från synvinkeln för svept vinkel, istället för att göra det från valvet. I ett sådant fall talar vi om vinkelhastighet. För en rörelse på en radieomkrets R, det finns ett samband mellan båge (i radianer) och vinkel:

s = R θ

Avleda med avseende på tid på båda sidor:

ds / dt = R (dθ/ dt)

Kallar derivatet av θ med avseende på t Vad vinkelhastighet och betecknar det med den grekiska bokstaven ω "omega", vi har detta förhållande:

v = ωR

Centripetal acceleration

Alla cirkulära rörelser har centripetal acceleration, som alltid är riktad mot centrum av omkretsen. Hon ser till att hastigheten ändras för att röra sig med partikeln när den roterar.

Centripetal acceleration till_c eller till_R pekar alltid mot mitten (se figur 2) och är relaterad till linjär hastighet så här:

till_c = v^två / R

Och med vinkelhastigheten som:

till_c = (ωR)^två / R = ω^tvåR

För enhetlig cirkelrörelse, positionen s (t) är av formen:

s (t) = så + vt

Dessutom måste den varierade cirkelrörelsen ha en komponent av acceleration som kallas tangentiell acceleration till_T, som handlar om att ändra storleken på linjär hastighet. Ja till_T  det är konstant, positionen är:

s (t) = s_eller + v_ellert + ½ a_Tt^två

Med v_eller som initialhastighet.

Löste problem med linjär hastighet

De lösta övningarna hjälper till att klargöra korrekt användning av begreppen och ekvationerna ovan..

-Löst övning 1 

En insekt rör sig på en halvcirkel med radien R = 2 m, med start från vila vid punkt A medan den ökar sin linjära hastighet, med en hastighet av p m / s^två. Hitta: a) Efter hur länge den når punkt B, b) Linjär hastighetsvektor vid det ögonblicket, c) Accelerationsvektorn vid det ögonblicket.

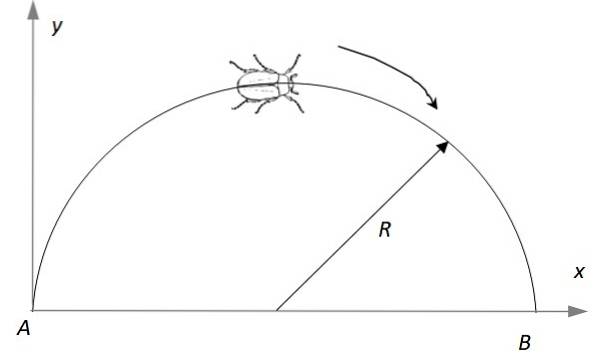
Lösning

a) Uttalandet indikerar att den tangentiella accelerationen är konstant och är lika med π m / s^två, då är det giltigt att använda ekvationen för jämnt varierad rörelse:

s (t) = s_eller + v_ellert + ½ a_T.t^två

Med s_eller = 0 och v_eller = 0:

s (t) = ½ a_T.t^två

s = πR (Halva längden på omkretsen)

t = (2. πR /till_T) ^½ s = (2π.2 / π)^½s = 2 s

b) v (t) = v_eller + till_T. t = 2π Fröken

När vid punkt B pekar den linjära hastighetsvektorn i vertikal riktning nedåt i riktningen (-Y):

v (t) = 2π Fröken(-Y)

c) Vi har redan den tangentiella accelerationen, centripetalacceleration saknas för att ha hastighetsvektorn till:

till_c = v^två / R = (2π)^två / 2 m / s^två = 2π^två Fröken^två

till = a_c (-x) + a_T (-Y) = 2π^två(-x) + π (-Y) Fröken^två

-Övning löst 2

En partikel roterar i en cirkel av 2,90 m. Vid ett visst ögonblick är accelerationen 1,05 m / s^två i en sådan riktning att den bildar 32º med sin rörelseriktning. Hitta dess linjära hastighet vid: a) Detta ögonblick, b) 2 sekunder senare, förutsatt att den tangentiella accelerationen är konstant.

Lösning

a) Rörelseriktningen är just den tangentiella riktningen:

till_T = 1,05 m / s^två . cos 32º = 0,89 m / s^två ; till_C = 1,05 m / s^två . sin 32º = 0,56 m / s^två

Hastigheten rensas från till_c = v^två / R Vad:

v = (R.a_c)^1/2  = 1,27 m / s

b) Följande ekvation gäller för jämnt varierad rörelse: v = v_eller + till_Tt = 1,27 + 0,89,2^två m / s = 4,83 m / s

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physics Series for Sciences and Engineering. Volym 3: e. Utgåva. Kinematik. 199-232.
3. Giancoli, D. 2006. Fysik: principer med tillämpningar. 6^th... Ed Prentice Hall. 62-64.
4. Relativ rörelse. Återställd från: courses.lumenlearning.com
5. Wilson, J. 2011. Fysik 10. Pearson Education. 166-168.