
Andra förklaringen av jämviktstillstånd, exempel, övningar
De andra jämviktsförhållandet fastställer att summan av de vridmoment eller moment som alstras av alla krafter som verkar på en kropp, oavsett vilken punkt de beräknas, måste avbrytas så att kroppen är i statisk eller dynamisk jämvikt.
Betecknar vridmomentet eller kraftmomentet med den grekiska bokstaven τ, matematiskt uttrycks det så här:
∑ τ = 0

Den djärva bokstaven indikerar momentets vektornatur, som måste avbrytas med avseende på vilken punkt som helst som valts som rotationscentrum. Genom att avbryta nätmomentet säkerställs att objektet inte börjar rotera eller välta..
Om objektet redan roterade tidigare och nettomomentet plötsligt försvinner fortsätter rotationen, men med konstant vinkelhastighet.
Det andra jämviktsvillkoret används i samband med det första tillståndet, som säger att summan av krafterna på en kropp måste vara noll, så att den inte översätts, eller att om den gör det, är den med enhetlig rätlinjig rörelse:
∑ F = 0
Båda villkoren gäller för utvidgade kroppar, de vars dimensioner är mätbara. När ett objekt antas vara en partikel är det ingen mening att tala om rotationer, och det första villkoret är tillräckligt för att garantera jämvikt.
Exempel
Det andra jämviktsförhållandet avslöjas i otaliga situationer:
När du klättrar uppför stegen
När vi stöder en stege på golvet och väggen behöver vi tillräckligt med friktion, särskilt på golvet, för att säkerställa att stegen inte glider. Om vi försöker klättra på en stege som stöds på ett oljigt, vått eller hal golv är det inte svårt att förutse att vi kommer att falla.
För att kunna använda stegen med tillförsikt är det nödvändigt att den är i statisk balans när du klättrar och när den är på önskad steg.
Flytta en garderob
När du vill flytta en hög möbel som en garderob eller någon annan bit vars höjd är större än dess bredd är det bekvämt att trycka på en låg punkt för att undvika att välta, på detta sätt är det mer troligt att möbler glider istället för att vända sig och lägga sig.
Under sådana omständigheter är möblerna inte nödvändigtvis i jämvikt, eftersom de kan röra sig snabbt, men åtminstone skulle det inte välta.
Balkonger
Balkongerna som sticker ut från byggnaderna ska byggas så att även om det finns många människor på toppen, välter det inte och kollapsar.
Dielektriker i externa elektriska fält
Genom att placera ett dielektriskt material i ett externt elektriskt fält rör sig och roterar molekylerna tills de intar en jämviktsposition, vilket skapar ett elektriskt fält inuti materialet..
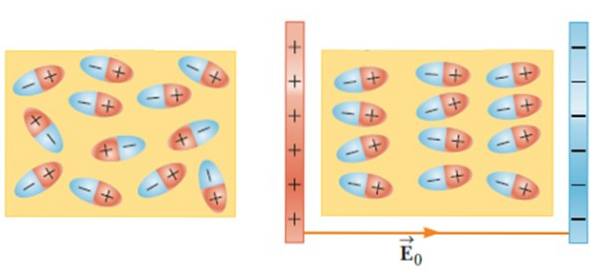
Denna effekt ökar kapaciteten hos en kondensator när ett material som glas, gummi, papper eller olja sätts in mellan dess ramar..
Skyltar och lampor
Det är vanligt att många lokalbefolkningen hänger meddelanden på byggnadens vägg så att de är synliga för förbipasserande.
Affischen hålls av en stång och en kabel, båda fästa vid väggen med fästen. De olika krafterna som verkar måste se till att affischen inte faller, för vilken de två jämviktsförhållandena spelar in.
En reflektor kan också placeras på detta sätt i en park, som i följande bild:
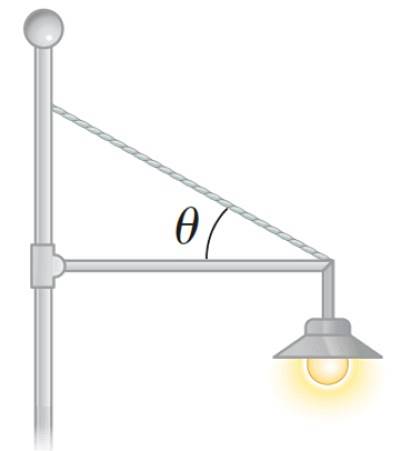
Hur man beräknar nettomomentet eller nettomomentet för en kraft?
Momentet eller momentet för en kraft, betecknad med τ eller M i vissa texter beräknas det alltid med avseende på någon punkt där rotationsaxeln passerar.
Det definieras som vektorprodukten mellan positionsvektorn r, som styrs från nämnda axel till kraftens och kraftens appliceringspunkt F:
τ = r × F
Att vara en vektor är det nödvändigt att uttrycka vridmomentet genom att ge dess storlek, riktning och känsla. Storleken ges av:
τ = rF.sen θ
Högerhandregel för vektorprodukt
När problemet är i planet är vridmomentets riktning vinkelrätt mot papperet eller skärmen och riktningen bestäms av högerregeln, i vilken pekfingret pekar mot r, långfingret mot F och tummen pekar in eller ut ur papperet.
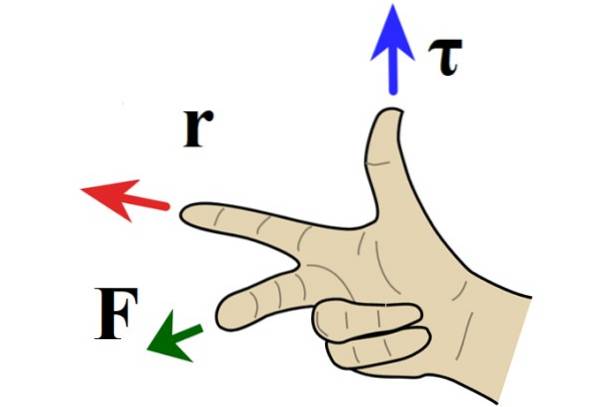
När vridmomentet pekar ut ur papperet, roteras moturs och tilldelas ett positivt tecken enligt konventionen. Om vridmomentet istället riktas mot bladets insida är rotationen medurs och negativ..
För att hitta nettomomentet väljs en lämplig punkt för beräkningen, som kan vara den vid vilken den största mängden krafter verkar. I detta fall är momentet för dessa krafter noll, eftersom det har en positionsvektor r av storlek 0.
Du kan välja vilken punkt som helst som ger tillräckligt med information för att lösa det okända som ber om att problemet ska lösas. Låt oss se det mer detaljerat nedan.
Övningen löst
Reflektorn i följande figur har en massa på 20 kg och stöds av en tunn horisontell stång, med försumbar massa och längd L, som är ledad till en stolpe. Kabeln, även lätt, som hjälper till att stödja reflektorn bildar en vinkel θ = 30º mot stången. Beräkna:
a) Spänningen i kabeln
b) Storleken på kraften F som stolpen utövar på stången genom gångjärnet.
Lösning
Vi kommer att tillämpa det första jämviktsvillkoret ∑ F = 0 till de krafter som visas i diagrammet:
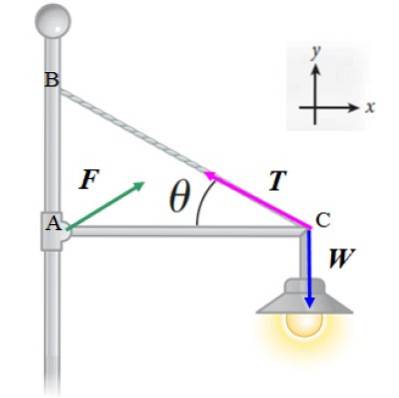
F + T + W = 0
Observera att storleken och riktningen på F är ännu inte fastställda, men vi antar att den har två komponenter: Fx och FY. På detta sätt får vi två ekvationer:
Fx -T. cos θ = 0
FY - W + T⋅ sin θ = 0
Låt oss nu tillämpa det andra jämviktsvillkoret, välja punkt A, eftersom vi inte vet storleken på F inte heller den av T. Genom att välja denna punkt, vektorn rTILL är noll, därför F är noll och storleken på F visas inte i ekvationen:
-W⋅L + T⋅sen θ⋅L = 0
Därför:
T.sen θ.L = W.L
T = W / sin θ = (20 kg x 9,8 m / stvå) / Sin 30º = 392 N
Att veta storleken på T vi kan lösa för komponenten Fx:
Fx = T⋅ cos θ = 392 cos 30º N = 339. 5 N
Och sedan komponent FY:
FY = W - T⋅ sin θ = (20 kg x 9,8 m / stvå) - 392⋅sin 30º = 0
Då kan vi uttrycka F Så:
F = 339,5 N x
Det är därför en horisontell kraft. Detta beror på att vi ansåg att stången hade försumbar vikt.
Om punkt C hade valts för att beräkna det resulterande ögonblicket, vektorerna rT Y rW är noll, därför:
M = FochL = 0
Det dras slutsatsen att FY = 0. På detta sätt:
- W + T⋅ sin θ = 0
T = W / sin θ
Vilket är samma resultat som ursprungligen erhölls vid val av punkt A som den plats där rotationsaxeln passerar.
Teman av intresse
Jämviktsförhållanden.
Första jämviktsförhållandet.
Referenser
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 4. Partikelsystem. Redigerad av Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Utg. Volym 1.
- Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7: e. Ed. Cengage Learning.



Ingen har kommenterat den här artikeln än.