De ekuationssystem De består av två eller flera ekvationer med flera variabler som måste ha en gemensam lösning. De är frekventa, eftersom det i praktiken finns många situationer som beror på många faktorer, som är relaterade på olika sätt.
Generellt har ett ekvationssystem följande form, där varje funktion representerar ett av de villkor som lösningen måste uppfylla:
Låt oss se ett exempel: antar att du behöver göra rektangulära pappersark vars yta är 180 cmtvå och som har en omkrets på 54 cm. Vad ska vara måtten på arket?
För att svara på frågan tar vi hänsyn till att dimensionerna på ett rektangulärt ark är två: bredd och höjd. Det betyder att vi har två variabler som vi kommer att ge de vanliga namnen på x och Y.
Och dessa variabler måste uppfylla de två villkor som ställs samtidigt:
-Första villkoret: arket är 180 cmtvå. Detta blir den första funktionen: F1.
-Andra villkor: arkets omkrets eller kontur måste vara 54 cm. Detta är den andra funktionen Ftvå.
För varje tillstånd upprättas en ekvation med algebraiskt språk. Området A för ett rektangulärt ark erhålls genom att multiplicera bredden med höjden:
A = x.y = 180 cmtvå
Och omkretsen P är resultatet av att lägga till sidorna. Eftersom omkretsen är summan av sidorna:
P = 2x + 2y = 54 cm
Det resulterande systemet med två ekvationer och två okända är:
xy = 180
2 (x + y) = 54
Vi behöver två siffror vars produkt är 180 och den dubbla produkten av deras summa är 54, eller vad är detsamma: tillsammans måste de ge 27. Dessa siffror är 12 och 15.
I avsnittet med lösta övningar kommer vi att erbjuda den detaljerade metoden för att hitta dessa värden, medan läsaren enkelt kan verifiera genom att ersätta att de effektivt uppfyller båda ekvationerna.
Artikelindex
Situationen som föreslås ovan innehåller två variabler, och minst två ekvationer krävs för att hitta dem. Det finns system med många fler variabler, men i vilket fall som helst om systemet har n av dem kräver det åtminstone n ekvationer oberoende av varandra (man kan inte vara en linjär kombination av de andra) för att hitta lösningen, om den existerar.
När det gäller applikationerna är de många. Här är några i vilka ekvationssystem visar att de är användbara:
-Hitta strömmar som flyter genom en krets med Kirchoffs lagar.
-I land- och lufttransport för att fastställa avgångs- och ankomsttider.
-Hitta krafternas storlek i dynamiska eller statiska system som är föremål för flera interaktioner.
-Att veta mängden föremål som sålts under en viss tidsperiod, eller i fabriker, för att bestämma måtten på föremål så att de uppfyller vissa villkor när det gäller yta eller volym.
-När man bestämmer hur man ska fördela ett kapital i olika investeringar.
-Fastställ priserna för olika tjänster, till exempel telekommunikation eller program och känn hur mycket pengar som samlas in (se löst exempel 2)
-En ekvation väljs och en av variablerna löses.
-Då måste vi ersätta den rensade variabeln i en annan ekvation. Sedan försvinner denna variabel därifrån och om systemet har två ekvationer och två okända, finns det en ekvation med en variabel som redan kan lösas.
-Om systemet har mer än två variabler måste vi lösa en tredje okänd från en annan ekvation och ersätta den också.
Ett exempel på tillämpningen av denna metod är i löst övning 1.
Denna metod består av att addera eller subtrahera ekvationer för att eliminera en eller flera variabler och bara lämna en. För att göra detta är det bekvämt att multiplicera ekvationerna med en faktor så att det okända försvinner när man adderar med en annan ekvation. Låt oss se ett exempel:
3xtvå - Ytvå = 11
xtvå + 4ytvå = 8
Vi multiplicerar den första ekvationen med 4:
12xtvå - 4ytvå = 44
xtvå + 4ytvå = 8
Genom att lägga till dem försvinner det okända Y, återstående:
13xtvå = 52
xtvå = 4
Därför x1 = 2 och xtvå = -2. Med dessa värden kan läsaren kontrollera det och1 = 1 och ytvå = -1
När systemet är två ekvationer med två okända:
-Välj ett okänt och lösa för båda ekvationerna.
-Resultaten utjämnas, vilket gör det möjligt att få en enda ekvation med en enda okänd.
-Denna ekvation är löst och resultatet ersätts i en av de tidigare avstånden för att erhålla värdet på den andra okända..
Denna metod kommer att tillämpas i löst övning 2 i följande avsnitt.
Denna metod består av att kurva kurvorna som varje ekvation representerar. Skärningspunkten är lösningen på systemet. Följande exempel visar systemets grafiska lösning:
xtvå + Y två = 1
2x + 4y = 0
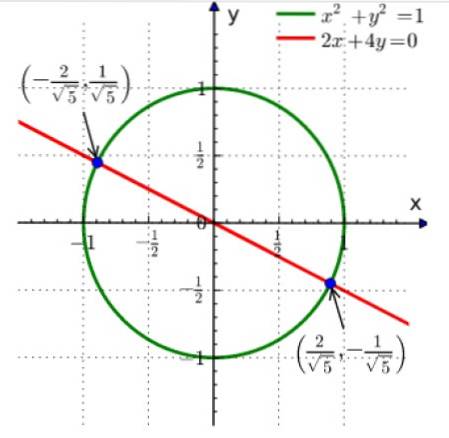
Den första ekvationen är en cirkel med radie 1 centrerad vid ursprunget och den andra är en linje.
Korsningen av båda är de två punkterna som visas i blått. Läsaren kan verifiera att genom att ersätta koordinaterna för punkterna i ovanstående ekvationer erhålls en jämlikhet.
Du måste göra rektangulära pappersark med en yta på 180 cmtvå och med en omkrets på 54 cm. Vad ska vara måtten på arket?
Systemet att lösa är:
xy = 180
2 (x + y) = 54
Den andra ekvationen kan förenklas till x + y = 27, därför:
xy = 180
x + y = 27
Lös för en av de okända i den andra ekvationen:
y = 27 - x
Clearance ersätts i det första:
(27 -x) = 180
Tillämpa distribuerande egendom:
-xtvå + 27x = 180
Multiplicera med (-1) på båda sidor av ekvationen och skicka 180 till vänster:
xtvå - 27x +180 = 0
Resultatet är en ekvation av andra graden i x, som löses med formeln:
Med a = 1, b = -27 och c = 180
En nöjespark har följande entréavgifter: barn $ 1,5 och vuxna $ 4. På en dag var det 2200 besökare, vilket samlade in 5050 dollar. Hitta antalet barn och vuxna som besökte parken den dagen.
Vara x antalet barn och Y antalet vuxna. Vi kan fastställa den första av ekvationerna med vetskap om att summan av båda måste vara 2200:
x + y = 2200.
Nu går vi med de insamlade pengarna. Priset på barnbiljetten är 1,5 USD för varje barn, genom att multiplicera detta värde med x, antalet barn, har vi beloppet för barnbiljetten:
1,5x = insamlade pengar för barnbiljetter
Och om vi multiplicerar 4 dollar per vuxen med antalet och antalet vuxna besökare får vi de totala pengarna för alla vuxna:
4y = pengar som samlas in av vuxenbiljetter
Vi lägger till detta tillsammans för att få $ 5050:
1,5x + 4y = 5050
Vårt ekvationssystem är:
x + y = 2200
1,5x + 4y = 5050
Låt oss lösa det genom utjämning. Vi isolerar variabeln y från den första och den andra ekvationen:
y = 2200 - x
y = (5050 - 1,5 x) / 4
Vi matchar båda uttrycken:
2200 - x = (5050 - 1,5x) / 4
Vi multiplicerar allt med 4 för att eliminera bråk:
8800 - 4x = 5050 - 1,5x
Vi grupperar termerna med x till vänster och de rena siffrorna till höger:
-4x + 1,5x = 5050 - 8800
-2,5x = -3750
x = 1500 barn.
Vi ersätter detta värde i y = 2200 - x för att hitta antalet vuxna:
y = 2200 - 1500 = 700 vuxna.
Ingen har kommenterat den här artikeln än.