Steiners satsförklaring, tillämpningar, övningar

De Steiners sats, också känd som sats för parallella axlar, gör det möjligt att utvärdera tröghetsmomentet för en utsträckt kropp, runt en axel som är parallell med en annan som passerar genom objektets masscentrum.

Det upptäcktes av den schweiziska matematikern Jakob Steiner (1796-1863) och säger följande: låt jag_CENTIMETER tröghetsmomentet för objektet med avseende på en axel som passerar genom dess masscentrum CM och I_z tröghetsmomentet med avseende på en annan axel parallell med detta.

Att känna avståndet D som skiljer båda axlarna och massan M för kroppen i fråga, är tröghetsmomentet med avseende på den okända axeln:

Jag_z = Jag_CENTIMETER + MD^två

Tröghetsmomentet indikerar hur lätt det är för ett objekt att rotera runt en viss axel. Det beror inte bara på kroppens massa utan på hur den fördelas. Av denna anledning är det också känt som rotationsinerti, är sina enheter i International System Kg. m^två.

Satsen visar att tröghetsmomentet Jag_z är alltid större än tröghetsmomentet Jag_CENTIMETER i ett belopp som ges av M.D^två.

Artikelindex

• 1 applikationer
  • 1.1 Bevis på Steiners sats
• 2 Lösta övningar
  • 2.1 -Löst övning 1
  • 2.2 -Löst övning 2
• 3 Referenser

Applikationer

Eftersom ett objekt kan rotera runt många axlar, och i tabellerna generellt ges endast tröghetsmomentet i förhållande till axeln som passerar genom centroiden, underlättar Steiners sats beräkningen när det är nödvändigt att rotera kroppar kring axlar som inte matcha detta.

Till exempel roterar en dörr vanligtvis inte runt en axel som passerar genom dess masscentrum, utan kring en lateral axel, där gångjärnen fäster..

Genom att känna tröghetsmomentet är det möjligt att beräkna den kinetiska energi som är associerad med rotationen kring axeln. Ja K är den kinetiska energin, Jag tröghetsmomentet runt axeln i fråga och ω vinkelhastigheten är det nöjd med att:

K = ½ I.ω^två

Denna ekvation ser mycket ut som den mycket välbekanta formeln för kinetisk energi för ett massföremål M rör sig i hastighet v:  K = ½ M.v^två. Och det är att tröghetsmomentet eller rotationsinerti Jag spelar samma roll i rotation som massa M i översättning.

Bevis på Steiners sats

Tröghetsmomentet för ett utökat objekt definieras som:

Jag = ∫r^två dm

Var dm är en oändlig del av massan och r är avståndet mellan dm och rotationsaxeln z. I figur 2 passerar denna axel centrumet för massan CM, men den kan vara vilken som helst.

Runt en annan axel  z ', Tröghetsmomentet är:

Jag_z= ∫ (r ')^två dm

Nu, enligt triangeln som bildas av vektorerna D, r Y r ' (se figur 2 till höger), det finns en vektorsumma:

r + r ' = D   → r ' = D - r

De tre vektorerna ligger på objektets plan som kan vara xy. Koordinatsystemets ursprung (0,0) väljs i CM för att underlätta beräkningarna som följer.

På detta sätt den kvadrerade modulen för vektorn r ' det är:

(r ')^två = (D_x- r_x)^två +(D_Y - r_Y)^två =

= D_x^två + D_Y^två +r_x^två + r_Y2 -2D_xr_x - 2 D_Yr_Y =

= D^två + r^två  - 2D_xr_x - 2 D_Yr_Y

Nu ersätts denna utveckling i integralen av tröghetsmomentet I_z och även definitionen av densitet dm = ρ.dV används:

Termen M. D^två som visas i Steiners sats kommer från den första integralen, den andra är tröghetsmomentet med avseende på axeln som passerar genom CM.

Å andra sidan är den tredje och fjärde integralen värd 0, eftersom de per definition utgör positionen för CM, som har valts som ursprung för koordinatsystemet (0,0).

Lösta övningar

-Löst övning 1

Den rektangulära dörren i figur 1 har en massa på 23 kg, 1,30 bred och 2,10 m hög. Bestäm tröghetsmomentet för dörren i förhållande till axeln som går genom gångjärnen, förutsatt att dörren är tunn och enhetlig.

Lösning

Från en tabell över tröghetsmomenter, för en rektangulär platta med massa M och dimensioner till Y b, Tröghetsmomentet med avseende på axeln som passerar genom dess masscentrum är:_CENTIMETER = (1/12)M(till^två + b^två).

En homogen grind antas (en approximation, eftersom grinden i figuren förmodligen inte är så). I ett sådant fall passerar masscentrum genom dess geometriska centrum. I figur 3 har en axel som passerar genom massacentret ritats och är också parallell med axeln som passerar genom gångjärnen.

Jag_CENTIMETER = (1/12) x 23 kg x (1,30^två+2.10^två) m^två = 11,7 kg.m^två

Tillämpa Steiners sats för den gröna rotationsaxeln:

Jag = jag_CENTIMETER + MD^två = 11,7 kg.m^två + 23 kg x 0,652 m^två = 21,4 kg.

-Övning löst 2

Hitta tröghetsmomentet för en homogen tunn stav när den roterar kring en axel som passerar genom ena änden, se figur. Är det större eller mindre än tröghetsmomentet när det roterar runt centrum? Varför?

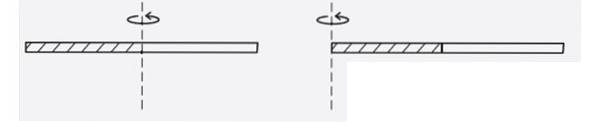
Lösning

Enligt tabellen över tröghetsmoment, tröghetsmomentet Jag_CENTIMETER av en tunn degstav M och längd L det är: Jag_CENTIMETER = (1/12) ML^två

Och Steiners sats säger att när den roteras runt en axel som passerar genom ena änden D = L / 2 förblir den:

Jag = jag_CENTIMETER + MD^två = (1/12) ML^två + M (L / 2)^två = (1/3) ML^två

Det är större, men inte bara två gånger utan 4 gånger mer, eftersom den andra halvan av stången (inte skuggad i figuren) roterar och beskriver en större radie.

Påverkan av avståndet till rotationsaxeln är inte linjärt utan kvadratiskt. En massa som är dubbelt så långt än en annan kommer att ha ett tröghetsmoment som är proportionellt mot (2D)^två = 4D^två.

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 313-340.
2. Georgia State University. Rotationsrörelse. Återställd från: phys.nthu.edu.tw.
3. Parallell axelteorem. Återställd från: hyperphysics.phy-astr.gsu.edu.
4. Rex, A. 2011. Grundläggande fysik. Pearson. 190-200.
5. Wikipedia. Sats för parallellaxel. Återställd från: en.wikipedia.org