
Historia trianglar, element, klassificering, egenskaper

De trianglar De är plana och slutna geometriska figurer, bestående av tre sidor. En triangel bestäms av tre linjer som korsar två och två och bildar tre vinklar med varandra. Den triangulära formen, full av symbolik, finns i otaliga objekt och som ett element i konstruktionen.
Ursprunget till triangeln går förlorat i historien. Från arkeologiska bevis är det känt att den primitiva mänskligheten visste det väl, eftersom arkeologiska kvarlevor bekräftar att den användes i verktyg och vapen.

Det är också tydligt att de forntida egyptierna hade en gedigen kunskap om geometri och särskilt om den triangulära formen. De återspeglades i de arkitektoniska elementen i dess monumentala byggnader.
I Rhind-papyrus finns formler för beräkning av trianglar och trapetsarealer, liksom vissa volymer och andra begrepp för rudimentär trigonometri.
För sin del är det känt att babylonierna kunde beräkna triangelns yta och andra geometriska figurer, som de använde för praktiska ändamål, till exempel landdelningar. De var också kunniga om många egenskaper hos trianglar.
Det var dock de forntida grekerna som systematiserade många av de geometriska begrepp som råder idag, även om mycket av denna kunskap inte var exklusiv, eftersom den säkert delades med dessa andra forntida civilisationer..
Artikelindex
- 1 Element av triangeln
- 1.1 Notation
- 2 typer av trianglar
- 2.1 Kongruens av trianglar
- 2.2 Likheter mellan trianglar
- 3 fastigheter
- 4 satser
- 4.1 Thales första sats
- 4.2 Thales andra sats
- 4.3 Pythagoras teorem
- 5 Området för en triangel
- 6 Exempel på trianglar
- 6.1 Exempel 1
- 6.2 Exempel 2
- 6.3 Exempel 3
- 7 övningar
- 7.1 Övning 1
- 7.2 Övning 2
- 8 Referenser
Triangel element
Elementen i vilken triangel som helst indikeras i följande bild. Det finns tre: hörn, sidor och vinklar.
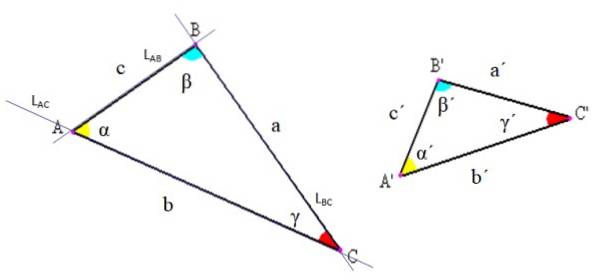
-Hörn: är skärningspunkterna för linjerna vars segment bestämmer triangeln. I figuren ovan, till exempel, linjen LAC som innehåller segmentet AC, skär linjen LAB innehållande segment AB precis vid punkt A.
-Sidor: mellan varje hörnpar ritas ett linjesegment som utgör en sida av triangeln. Detta segment kan betecknas med slutbokstäverna eller genom att använda en specifik bokstav för att kalla det. I exemplet i figur 2 kallas även sida AB "c".
-Vinklar: Mellan varje sida med en gemensam topp kommer en vinkel ut, vars topp sammanfaller med triangelns. I allmänhet betecknas vinkeln med en grekisk bokstav, som man sa i början.
För att bygga en viss triangel, med en given form och storlek, har du bara en av följande datamängder:
-Alla tre sidorna, ganska uppenbara för en triangel.
-Två sidor och vinkeln mellan dem och omedelbart dras den återstående sidan.
-Två (inre) vinklar och sidan mellan dem. Vid förlängning dras de två saknade sidorna och triangeln är klar.
Notation
Generellt används i trekantnotering följande konventioner: hörn indikeras med stora latinska bokstäver, sidor med små latinska bokstäver och vinklar med grekiska bokstäver (se figur 2).
På detta sätt namnges triangeln enligt dess hörn. Till exempel är triangeln till vänster i figur 2 triangel ABC, och den till höger är triangel A'B'C '.
Det är också möjligt att använda andra notationer; till exempel betecknas vinkeln a i figur 2 som BAC. Observera att bokstaven i toppunkten går i mitten och bokstäverna skrivs moturs.
Andra gånger placeras en vagn för att beteckna vinkeln:
a = ∠A
Typer av trianglar
Det finns flera kriterier för klassificering av trianglar. Det vanligaste är att klassificera dem efter måttet på deras sidor eller efter måttet på deras vinklar. Beroende på måttet på deras sidor kan trianglarna vara: skalor, likbenade eller liksidiga:
-Scalene: dess tre sidor är olika.
-Likbent: har två lika sidor och en annan sida.
-Liksidig: alla tre sidorna är lika.

Enligt måttet på deras vinklar heter trianglarna så här:
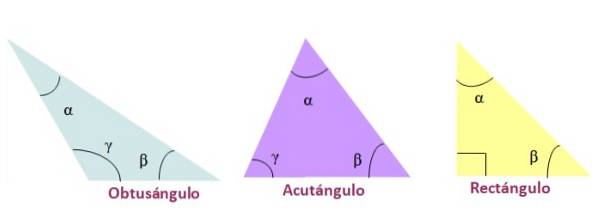
-Trubbig vinkel, om en av de inre vinklarna är större än 90 °.
-Spetsig vinkel, när triangelns tre inre vinklar är spetsiga, det vill säga mindre än 90 °
-Rektangel, om en av dess inre vinklar är 90º. Sidorna som bildar 90º kallas ben och sidan motsatt rät vinkel är hypotenusen..
Kongruens av trianglar
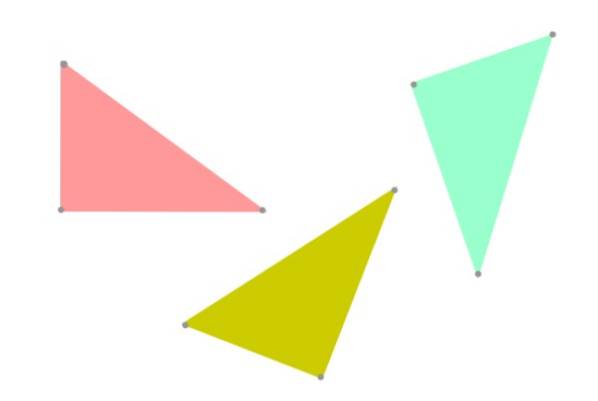
När två trianglar har samma form och har samma storlek, sägs de vara kongruenta. Naturligtvis är kongruens relaterat till jämlikhet, så varför i geometri talar vi om "två kongruenta trianglar" istället för "två lika trianglar"?
Tja, det föredras att använda termen "kongruens" för att hålla fast vid sanningen, eftersom två trianglar kan ha samma form och storlek, men vara orienterade annorlunda i planet (se figur 3). Ur geometriens synvinkel skulle de inte längre vara helt desamma.
Kongruenskriterier
Två trianglar är kongruenta om något av följande inträffar:
-Alla tre sidorna mäter samma (återigen är det mest uppenbara).
-De har två identiska sidor och med samma vinkel mellan sig.
-Båda har två identiska inre vinklar och sidan mellan dessa vinklar mäter densamma.
Som man kan se handlar det om att de två trianglarna uppfyller de nödvändiga förhållandena så att deras form och storlek är exakt samma när de byggs..
Kongruenskriterierna är mycket användbara, eftersom i praktiken måste otaliga bitar och mekaniska delar tillverkas i serie, på ett sådant sätt att deras mått och form är exakt samma.
Likhet mellan trianglar
En triangel liknar en annan om de har samma form, även om de har olika storlekar. För att säkerställa att formen är densamma krävs att de inre vinklarna har samma värde och att sidorna är proportionella..
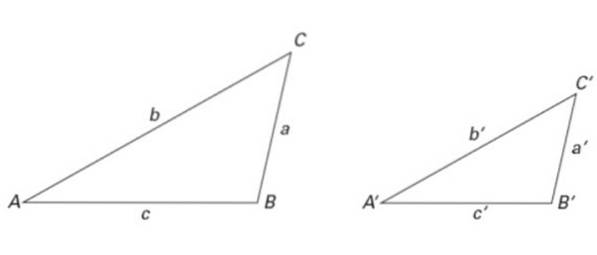
Trianglarna i figur 2 är också lika, liksom de i figur 6. På detta sätt:
∠ A = ∠ A ', ∠ B = ∠ B 'och ∠ C = ∠ C '
När det gäller sidorna gäller följande likhetsförhållanden:
a / a '= b / b' = c / c '
Egenskaper
De grundläggande egenskaperna hos trianglar är som följer:
-Summan av de inre vinklarna i en triangel är alltid 180º.
-För vilken triangel som helst är summan av dess yttre vinklar lika med 360 °.
- En yttre vinkel för en triangel är lika med summan av de två inre vinklarna som inte ligger intill nämnda vinkel.
Satser
Thales första sats
De tillskrivs den grekiska filosofen och matematikern Thales från Milet, som utvecklade flera satser relaterade till geometri. Den första av dem fastställer följande:
Om flera parallella linjer skär två tvärgående linjer bestäms segment som är proportionella i dem.
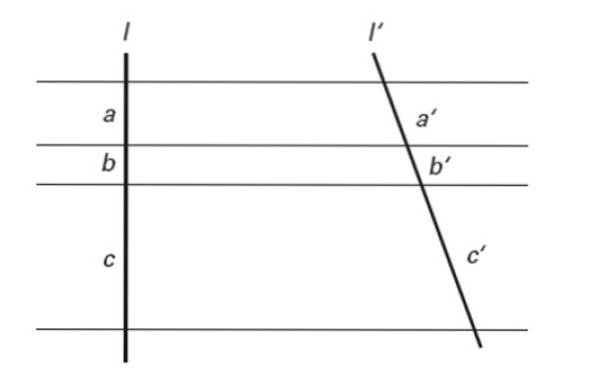
Med andra ord:
a / a '= b / b' = c / c '
Thales första sats är tillämplig på en triangel, till exempel har vi den blå triangeln ABC till vänster, som skärs av de röda parallellerna till höger:
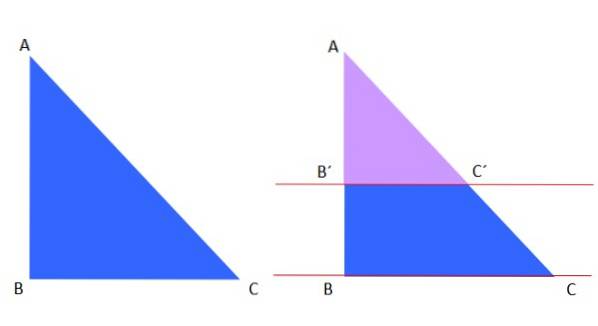
Den violetta triangeln AB'C 'liknar den blå triangeln ABC, enligt Thales' sats kan följande skrivas:
AB '/ AC' = AB / AC
Och det överensstämmer med vad som förklarades tidigare i segmentet av likheten mellan trianglar. Förresten, parallella linjer kan också vara vertikala eller parallella med hypotenusen och liknande trianglar erhålls på samma sätt.
Thales andra sats
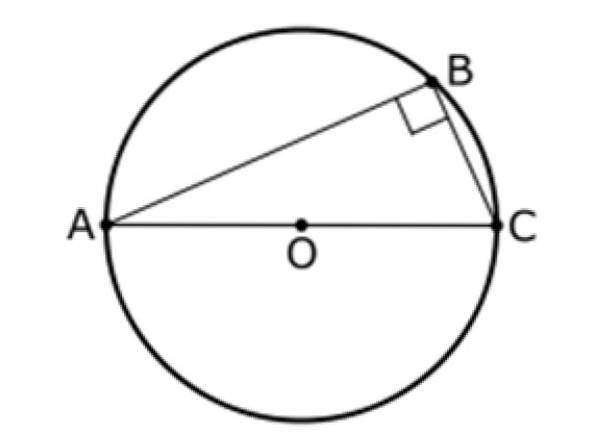
Denna sats hänvisar också till en triangel och en cirkel med centrum O, som de som visas nedan. I denna figur är AC en omkretsdiameter och B är en punkt på den, B skiljer sig från A och B.
Thales andra sats säger att:
Vinkeln mellan segmenten AB och BC är alltid 90º, därför är triangeln ABC rätt.
Pythagoras teorem
Detta är en av de mest kända satser i historien. Det beror på den grekiska matematikern Pythagoras från Samos (569 - 475 f.Kr.) och är tillämplig på en rätt triangel. Säger så:
Summan av kvadraterna i längderna på höger triangelns ben är lika med längden på hypotenusen i kvadrat.
Om vi tar ett exempel på den blå triangeln i figur 8, eller den violetta triangeln, eftersom båda är rektanglar, kan man säga att:
ACtvå = ABtvå + före Kristustvå (blå triangel)
AC 'två = AB 'två + FÖRE KRISTUS 'två (lila triangel)
Området för en triangel
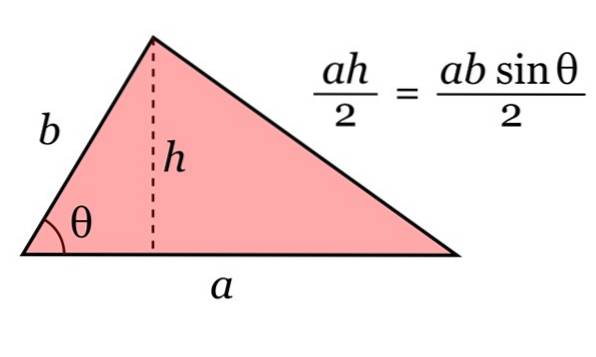
Området för triangeln ges av produkten av dess bas till och din längd h, dividerat med 2. Och med trigonometri kan denna höjd skrivas som h = b sinθ.
Exempel på trianglar
Exempel 1
Det sägs att med sin första sats lyckades Thales mäta höjden på den stora pyramiden i Egypten, ett av de antika världens 7 underverk, genom att mäta skuggan som den projicerade på marken och som projiceras av en stav drivs i marken..
Detta är beskrivningen av proceduren som följs av Tales:
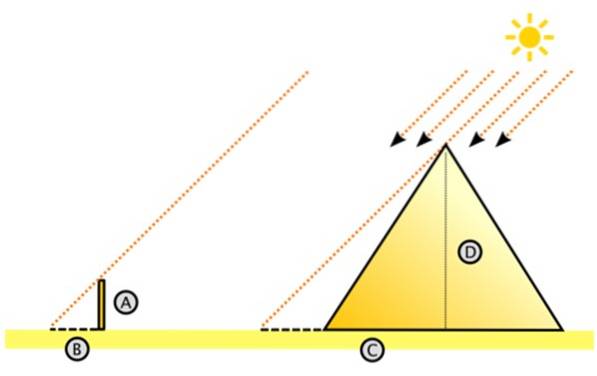
Thales antog korrekt att solens strålar slår parallellt. Med detta i åtanke föreställde han sig den stora högra triangeln till höger.
Där är D pyramidens höjd och C är avståndet över marken mätt från centrum till skuggan som kastas av pyramiden på ökenbotten. Det kan vara svårt att mäta C, men det är verkligen lättare än att mäta pyramidens höjd.
Till vänster är den lilla triangeln, med ben A och B, där A är höjden på staven som drivs vertikalt i marken och B är skuggan den kastar. Båda längderna är mätbara, liksom C (C är lika med längden på skuggan + halva pyramidens längd).
Så, av likheter av trianglar:
A / B = D / C
Och höjden på den stora pyramiden visar sig vara: D = C. (A / B)
Exempel 2
Takstolar i civil konstruktion är strukturer gjorda av korsade raka tunna stänger av trä eller metall, som används som stöd i många byggnader. De är också kända som gitter, fackverk eller gitter (fackverk på engelska).
I dem är trianglarna alltid närvarande, eftersom staplarna är sammankopplade vid punkter som kallas noder, som kan fixeras eller ledas..

Exempel 3
Metoden som kallas triangulering gör det möjligt att få plats för oåtkomliga punkter med kännedom om andra avstånd som är lättare att mäta, förutsatt att en triangel bildas som inkluderar den önskade platsen mellan dess hörn..
Till exempel, i följande figur vill vi veta var fartyget är i havet, betecknat som B.
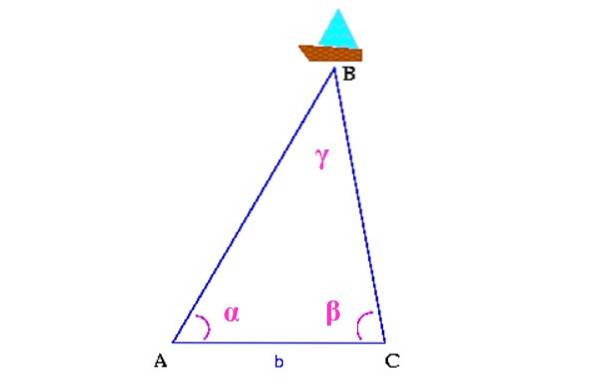
Först mäts avståndet mellan två punkter vid kusten, som i figuren är A och C. Därefter måste vinklarna α och β bestämmas med hjälp av en teodolit, en anordning som används för att mäta vertikala och horisontella vinklar.
Med all denna information byggs en triangel vars övre topp är fartyget. Det skulle förbli att beräkna vinkeln γ, med hjälp av trianglarnas egenskaper och avstånden AB och CB med hjälp av trigonometri, för att bestämma fartygets position i havet.
Träning
Övning 1
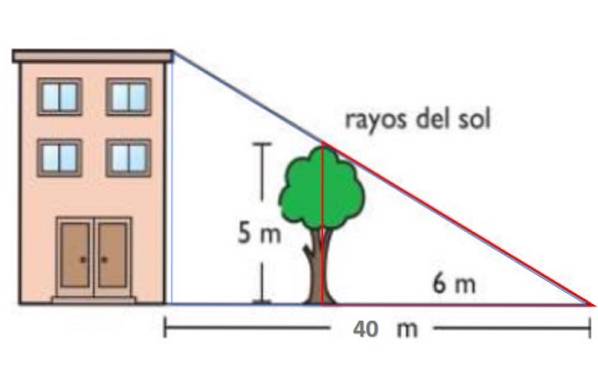
I den visade figuren är solens strålar parallella. På detta sätt kastar det 5 meter höga trädet en 6 meter skugga på marken. Samtidigt är byggnadens skugga 40 meter. Efter Thales första sats, hitta höjden på byggnaden.
Lösning
Den röda triangeln har sidor på 5 respektive 6 meter, medan den blå har höjd H - byggnadens höjd - och bas 40 meter. Båda trianglarna är lika, därför:
H / 40 = 5/6 → H = 40. (5/6) m = 33,3 m
Övning 2
Du måste känna till det horisontella avståndet mellan två punkter TILL Y B, men de ligger på en mycket ojämn mark.
Om mittpunkten (Pm) av detta land sticker ut en framträdande 1,75 meter hög. Om måttbandet anger 26 meters längd mätt från A till framträdande och 27 meter från B till samma punkt, hitta avståndet AB.
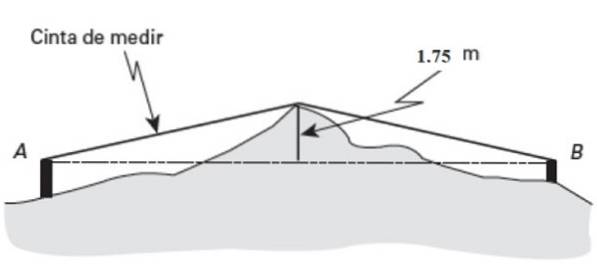
Lösning
Den pythagoreiska satsen tillämpas på en av de två högra trianglarna i figuren. Börjar med den till vänster:
Hypotenus = c = 26 meter
Höjd = a = 1,75 meter
APm = (26två - 1,75två)1/2 = 25,94 m
Applicera nu Pythagoras i triangeln till höger, den här gången c = 27 meter, a = 1,75 meter. Med dessa värden:
BPm= (27två - 1,75två)1/2 = 26,94 m
Avståndet AB hittas genom att lägga till följande resultat:
AB = 25,94 m + 26,94 m = 52,88 m.
Referenser
- Baldor, J. A. 1973. Plane and Space Geometry. Centralamerikansk kultur.
- Barredo, D. Triangelns geometri. Återställd från: ficus.pntic.mec.es.
- Jiménez, R. 2010. Matematik II. Geometri och trigonometri. Andra upplagan. Pearson.
- Wentworth, G. Plane Geometry. Återställd från: gutenberg.org.
- Wikipedia. Triangel. Återställd från: es. wikipedia.org.



Ingen har kommenterat den här artikeln än.