
Mackinder Box Vad det är för, hur man gör det och använder
De Mackinder låda det är ett metodiskt element med olika tillämpningar inom matematik. Hjälper till att lära dig grundläggande operationer: addition, subtraktion, multiplikation och division. Den används också för att separera delmängder av uppsättningar och för att subtrahera kardinaler; tjänar till att sönderdela och rekomponera tillsatsnummerstrukturer.
I grund och botten handlar det om att placera en central stor container och 10 mindre containrar runt den. Inom de mindre behållarna representeras enhetsmängder, som senare kommer att deponeras i en större behållare, för att representera att en kvantitet läggs till, med hänvisning till den progressiva tillsättningen eller multiplikationen.
Tvärtom kan det också representera att ett belopp dras ut från den större rutan, med hänvisning till uppdelningen.
Artikelindex
- 1 Vad är det för?
- 2 Hur man gör det?
- 2.1 Med kartonger
- 2.2 Med plastbehållare
- 2.3 Förfarande
- 3 Exempel på användning
- 3.1 Tillägg eller tillägg
- 3.2 Subtraktion eller subtraktion
- 3.3 Multiplikation
- 3.4 Uppdelning
- 4 Referenser
Vad är det för?
Mackinder-rutan är en metod som utvecklades 1918 i Chelsea, England, av Jessie Mackinder, som var lärare i den staden..
Denna metod syftar till att främja individualiseringen av utbildningen i ämnen som matematik, läsning och skrivning, med hjälp av enkla men intressanta material som behållare, kort och väskor, som används fritt..
Detta instrument består av tio containrar som omger en större central container, alla placerade på en plan bas. Dessa element används för att göra grundläggande matematiska operationer, såsom att addera, subtrahera, multiplicera och dela. Kan också användas för att separera uppsättningar och delmängder.
Lådan Mackinder används under de första åren av utbildning. Det underlättar förståelsen av matematik eftersom dess metodologi baseras på användningen av didaktiska material, vilket ger varje deltagares frihet att manipulera eller interagera direkt med materialet.
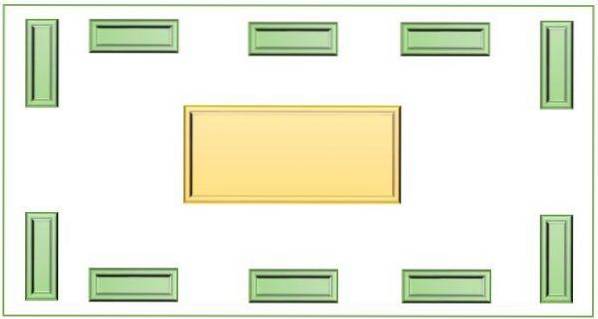
Hur man gör det?
Mackinder-lådan består av mycket grundläggande element. För att forma det kan du till och med använda återvinningsmaterial eller vilken typ av behållare som helst för att placera små föremål som representerar de enheter som kommer att räknas. Bland de vanligaste sätten att göra det är följande:
Med kartonger
Följande material kommer att behövas:
- En rektangulär bas, som kan vara gjord av kartong (skokartong) eller kartong.
- 10 små kartonger. De kan vara tändsticksaskar.
- 1 större låda.
- Lim.
- Tokens, tändstickor, frön eller pappersbollar som kan användas för att räkna.
Med plastbehållare
De material som ska användas är följande:
- En rektangulär bas, gjord av kartong (skokartong) eller kartong.
- Tio plastbehållare, håll dem små.
- En stor plastbehållare; till exempel ett CD-fodral.
- Lim.
- Tokens, tändstickor, frön eller pappersbollar som kan användas för att räkna.

Bearbeta
- Skär basen i en rektangulär form.
- Den största behållaren (kartongen eller plastbehållaren) är limmad i mitten.
- Mindre behållare limmas runt den stora behållaren och får torka.
- Behållare kan målas i olika färger och får torka.
- Flisen, tändstickor, frön, pappersbollar eller något annat som används för att räkna kan förvaras i en annan behållare eller inne i den centrala behållaren..
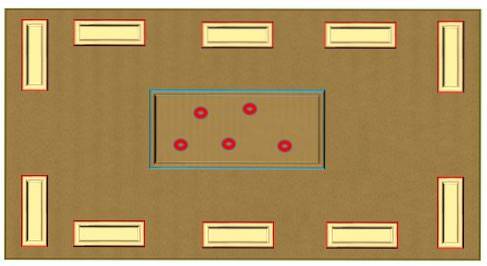
Exempel på användning
Med rutan Mackinder kan grundläggande matematiska operationer utföras, med hänsyn till att behållarna representerar grupper eller uppsättningar, medan elementen i var och en av dessa kommer att vara polletter, frön, papperskulor, bland andra..
Tillägg eller tillägg
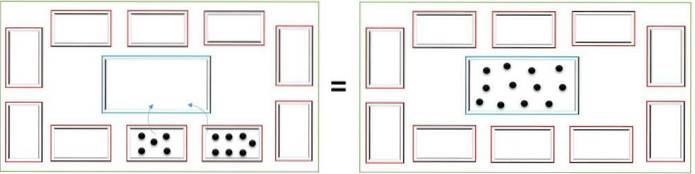
Två små lådor används för att göra en summa. I en av dessa placeras brickorna som representerar det första tillägget, och i den andra rutan placeras brickorna för det andra tillägget..
Du börjar räkna marker i rutan som har minst antal av dessa och de placeras i den centrala rutan; i slutet av brickorna från den första rutan, fortsätt med den andra.
Om du till exempel i en ruta har 5 brickor och i den andra 7, börjar du räkna från den med 5 brickor, placerar dem i den centrala rutan tills du når 5. Sedan fortsätter du med brickorna från den andra rutan och så fram till 12.
Subtraktion eller subtraktion
För att subtrahera alla brickor som representerar minuend placeras i den centrala rutan; det vill säga från det totala beloppet till vilket ett annat belopp kommer att subtraheras (subtraherande).
Från den stora rutan tas ut antalet marker som du vill subtrahera, de räknas och placeras i en av de små rutorna. För att veta resultatet av subtraktionen räknas antalet brickor som var kvar i den stora rutan.
Till exempel har du 10 brickor i den centrala rutan och du vill subtrahera 6 brickor. Dessa tas bort och placeras i en av de små lådorna; sedan, när man räknar brickorna som var kvar i den stora rutan, finns det totalt fyra brickor som representerar resultatet av subtraktionen.
Multiplikation
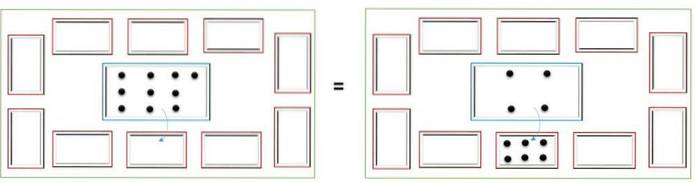
Multiplikation består av att lägga till samma nummer flera gånger. Med rutan Mackinder representerar det första talet i multiplikationen de grupper som kommer att bildas; det vill säga antalet små lådor som ska upptas.
Istället anger det andra numret antalet objekt som varje grupp kommer att ha, eller brickorna som ska placeras i varje liten låda. Sedan räknas alla brickor från varje liten låda och placeras i den centrala rutan för att få resultatet av multiplikationen.
Till exempel, för att multiplicera 4 x 3, placera 3 brickor i 4 små lådor; sedan börjar de räkna marker i den första rutan och placera dem i den stora rutan; detta upprepas med de 3 rutorna. I den centrala rutan kommer du att ha: 3 + 3 + 3 + 3 = 12 marker.
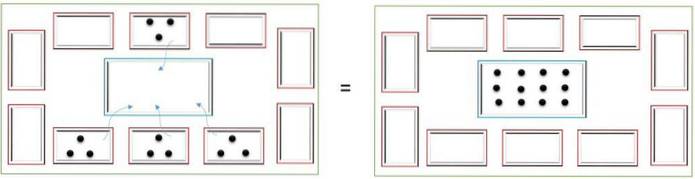
Division
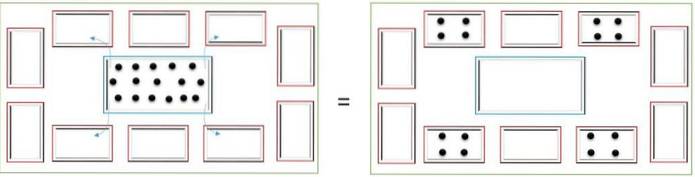
Uppdelning handlar om att dela ett antal element lika. För att till exempel dela upp 16 marker i fyra små lådor placeras dessa i den centrala lådan och de fördelas i små lådor på ett sådant sätt att samma mängd marker finns kvar i varje låda..
I slutet räknas antalet marker i varje ruta för att bestämma resultatet; i det här fallet kommer var och en att ha fyra marker.
Referenser
- Alicia Cofré, L. T. (1995). Hur man utvecklar matematisk logisk resonemang.
- Carolina Espinosa, C. C. (2012). Resurser för lärande.
- (1977). Allmän didaktik. Tupac.
- Mackinder, J. M. (1922). Individuellt arbete i spädbarnsskolor.
- María E. Calla, M. C. (2011). Lära sig logiska matematiska färdigheter hos flickor och pojkar. Lima: Educa.


Ingen har kommenterat den här artikeln än.