
Kapillaritetsegenskaper och exempel i vatten
De kapillaritet Det är en egenskap hos vätskor som gör att de kan röra sig genom rörformiga hål eller porösa ytor även mot tyngdkraften. För detta måste det finnas en balans och koordination mellan två krafter relaterade till vätskans molekyler: sammanhållning och vidhäftning; dessa två har en fysisk reflektion som kallas ytspänning.
Vätskan måste kunna blöta rörets inre väggar eller porerna i materialet genom vilket den rör sig. Detta inträffar när vidhäftningskraften (vätskekapillär rörvägg) är större än den intermolekylära sammanhållningskraften. Följaktligen skapar vätskans molekyler starkare interaktioner med materialets atomer (glas, papper, etc.) än med varandra..
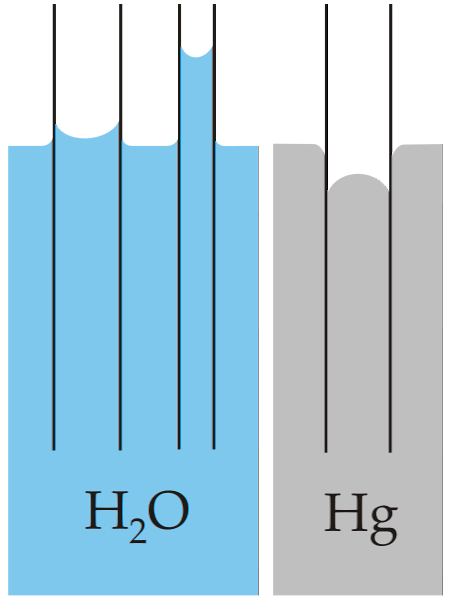
Det klassiska exemplet på kapillaritet illustreras genom att jämföra den här egenskapen för två väldigt olika vätskor: vatten och kvicksilver..
I bilden ovan kan det ses att vattnet stiger upp i rörets väggar, vilket innebär att det har större vidhäftningskrafter; medan med kvicksilver sker det motsatta, eftersom dess sammanhållningskrafter, av metallbindning, hindrar det från att fukta glaset.
Av denna anledning bildar vatten en konkav menisk och kvicksilver en konvex (kupolformad) menisk. Det bör också noteras att ju mindre rörets radie eller sektionen genom vilken vätskan färdas, desto större höjd eller sträcka som har rest (jämför höjden på vattenpelarna för båda rören).
Artikelindex
- 1 Kännetecken för kapillaritet
- 1.1 - Ytan på vätskan
- 1,2 -Höjd
- 1.3-Ytspänning
- 1.4 -Radius av kapillären eller poren genom vilken vätskan stiger
- 1,5 -Kontaktvinkel (θ)
- 2 Kapilläritet av vatten
- 2.1 I växter
- 3 Referenser
Kapillaritetsegenskaper
-Flytande yta
Vätskans yta, för att säga vatten, i en kapillär är konkav; menisken är konkav. Denna situation inträffar eftersom den resulterande kraften som utövas på vattenmolekylerna nära rörväggen är riktad mot detta.
I varje menisk finns en kontaktvinkel (θ), som är den vinkel som bildas av kapillärrörets vägg med en linje som tangerar vätskans yta vid kontaktpunkten..
Vidhäftning och sammanhållningskrafter
Om vätskans vidhäftningskraft till kapillärväggen råder över den intermolekylära sammanhållningskraften är vinkeln θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
När en droppe vatten placeras på ytan av ett rent glas sprider sig vattnet över glaset, så θ = 0 och cos θ = 1.
Om den intermolekylära sammanhållningskraften råder över vätskekapillärväggens vidhäftningskraft, till exempel i kvicksilver, kommer menisken att vara konvex och vinkeln θ får ett värde> 90 °; kvicksilver fuktar inte kapillärväggen och rinner därför nerför dess innervägg.
När en droppe kvicksilver placeras på ytan av ett rent glas behåller droppen sin form och vinkeln θ = 140º.
-Höjd
Vattnet stiger genom kapillärröret tills det når en höjd (h), där vikten på vattenpelaren kompenserar den vertikala komponenten i den intermolekylära sammanhållningskraften.
När mer vatten stiger kommer en punkt att tyngdkraften kommer att stoppa uppstigningen, även om ytspänningen fungerar till din fördel..
När detta händer kan molekylerna inte fortsätta att "klättra" på de inre väggarna, och alla fysiska krafter utjämnas. Å ena sidan finns de krafter som främjar uppgången av vattnet, och å andra sidan dess egen vikt som trycker ner det.
Jurins lag
Detta kan skrivas matematiskt enligt följande:
2 π rϒcosθ = ρgπrtvåh
Där den vänstra sidan av ekvationen beror på ytspänningen, vars storlek också är relaterad till sammanhållning eller intermolekylära krafter; Cosθ representerar kontaktvinkeln och r radien för hålet genom vilket vätskan stiger.
Och på höger sida av ekvationen har vi höjden h, tyngdkraften g och vätskans densitet; vad skulle vara vattnet.
Lösa sedan för h vi har
h = (2ϒcosθ / ρgr)
Denna formulering är känd som Jurins lag, som definierar höjden som nås av vätskekolonnen, i kapillärröret, när vikten av vätskekolonnen balanseras med uppstigningskraften genom kapillärverkan..
-Ytspänning
Vatten är en dipolmolekyl på grund av syreatomens elektronegativitet och dess molekylära geometri. Detta gör att den del av vattenmolekylen där syret är belägen blir negativt laddad, medan den del av vattenmolekylen som innehåller de två väteatomerna är positivt laddad..
Molekylerna i vätskan interagerar tack vare detta genom flera vätebindningar och håller dem ihop. Vattenmolekylerna i vattnet: luftgränssnittet (ytan) utsätts dock för en nettoattraktion av vätskans sinusmolekyler, vilket inte kompenseras av den svaga attraktionen med luftmolekylerna.
Därför utsätts vattenmolekylerna vid gränsytan för en attraktiv kraft som tenderar att avlägsna vattenmolekyler från gränsytan; det vill säga vätebindningarna som bildas med molekylerna längst ner drar de som finns på ytan. Således syftar ytspänningen till att minska ytan på vattnet: luftgränssnittet..
Förhållande med h
Om vi tittar på Jurins lagekvation, kommer vi att upptäcka att h är direkt proportionell mot ϒ; ju högre ytspänning vätskan har, desto större höjd kan stiga genom en kapillär eller por i ett material.
På detta sätt kan det förväntas att för två vätskor, A och B, med olika ytspänningar, kommer den med större ytspänning att stiga till en högre höjd..
Man kan dra slutsatsen med avseende på denna punkt att en hög ytspänning är den viktigaste egenskapen som definierar vätskans kapilläregenskap..
-Radie av kapillär eller por genom vilken vätskan stiger
Observationen av Jurins lag indikerar att höjden som en vätska når i en kapillär eller porer är omvänt proportionell mot samma radie.
Ju mindre radien är, desto större höjd når vätskekolonnen genom kapillaritet. Detta kan ses direkt på bilden där vatten jämförs med kvicksilver.
I ett glasrör med en radie på 0,05 mm radie når vattenpelaren per kapillaritet en höjd av 30 cm. I kapillärrör med en radie av 1 µm med ett sugtryck av 1,5 x 103 hPa (vilket är lika med 1,5 atm) motsvarar en beräkning av vattenpelarens höjd på 14 till 15 m.
Detta liknar mycket vad som händer med de sugrör som tänder på sig själva flera gånger. Genom att sippa vätskan skapas en tryckskillnad som får vätskan att stiga upp till munnen.
Den maximala höjden på kolonnen som uppnås genom kapillaritet är teoretisk, eftersom kapillärernas radie inte kan reduceras utöver en viss gräns..
Poiseuilles lag
Detta fastställer att flödet av en riktig vätska ges av följande uttryck:
Q = (πr4/ 8ηl) AP
Där Q är vätskeflödet, η är dess viskositet, l är rörets längd och AP är tryckdifferensen.
När en kapillärradie minskar bör höjden på vätskekolonnen som nås genom kapillärverkan öka på obestämd tid. Poiseuille påpekar dock att när radien minskar minskar också vätskeflödet genom denna kapillär..
Viskositet, som är ett mått på motstånd mot flödet av en riktig vätska, skulle också ytterligare minska vätskeflödet..
-Kontaktvinkel (θ)
Ju större värdet på cosθ, desto större är vattenpelarens höjd med kapillaritet, vilket indikeras av Jurins lag.
Om θ är liten och närmar sig noll (0) är cosθ = 1, så värdet h blir maximalt. Tvärtom, om θ är lika med 90º, är cosθ = 0 och värdet på h = 0.
När värdet på θ är större än 90 °, vilket är fallet med den konvexa menisken, stiger inte vätskan med kapillaritet och dess tendens är att sjunka (som sker med kvicksilver).
Kapilläritet av vatten
Vatten har ett ytspänningsvärde på 72,75 N / m, relativt högt jämfört med värdena för ytspänning för följande vätskor:
-Aceton: 22,75 N / m
-Etylalkohol: 22,75 N / m
-Hexan: 18,43 N / m
-Metanol: 22,61 N / m.
Därför har vatten en exceptionell ytspänning, vilket gynnar utvecklingen av det kapillaritetsfenomen som är så nödvändigt för att absorbera vatten och näringsämnen av växter..
I växterna

Kapillaritet är en viktig mekanism för uppstigningen av saften genom växternas xylem, men det är inte tillräckligt för att få saften till trädens löv..
Spiration eller avdunstning är en viktig mekanism vid uppstigningen av saft genom växternas xylem. Bladen tappar vatten genom avdunstning, vilket genererar en minskning av mängden vattenmolekyler, vilket orsakar en attraktion av de vattenmolekyler som finns i kapillärerna (xylem).
Vattenmolekyler agerar inte oberoende av varandra utan interagerar med Van der Waals-krafter, vilket får dem att stiga samman genom växternas kapillärer mot bladen.
Förutom dessa mekanismer bör det noteras att växter absorberar vatten från jorden genom osmos och att ett positivt tryck som alstras i roten driver början på uppgången av vatten genom växtens kapillärrör..
Referenser
- García Franco A. (2010). Ytliga fenomen. Återställd från: sc.ehu.es
- Ytfenomen: ytspänning och kapillaritet. [PDF]. Återställd från: ugr.es
- Wikipedia. (2018). Kapillaritet. Återställd från: es.wikipedia.org
- Risvhan T. (s.f.) Kapillaritet i växter. Återställd från: academia.edu
- Helmenstine, Anne Marie, Ph.D. (22 december 2018). Kapilläråtgärd: definition och exempel. Återställd från: thoughtco.com
- Ellen Ellis M. (2018). Kapillärverkan av vatten: definition och exempel. Studie. Återställd från: study.com
- ScienceStruck-personal. (16 juli 2017). Exempel som förklarar begreppet och betydelsen av kapilläråtgärd. Återställd från: sciencestruck.com


Ingen har kommenterat den här artikeln än.