Hur hittar man vinkeln på en triangel?

Det finns flera sätt att beräkna sidorna och vinklarna för en triangel. Dessa beror på vilken typ av triangel du arbetar med.

Vid denna möjlighet kommer det att visas hur man beräknar sidorna och vinklarna för en rätt triangel, förutsatt att vissa data i triangeln med kända.

Elementen som kommer att användas är:

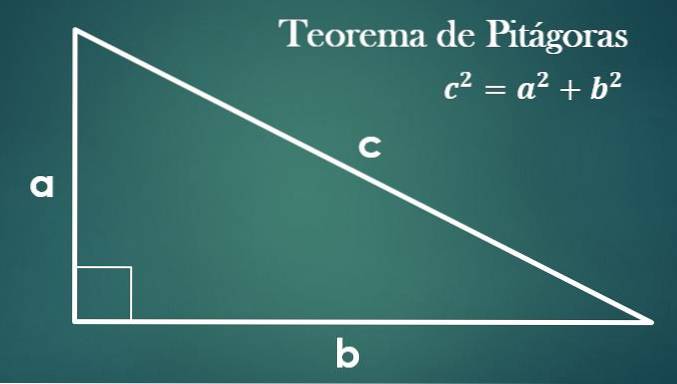
- Pythagoras teorem

Med tanke på en höger triangel med benen "a", "b" och hypotenus "c" är det sant att "c² = a² + b²".

- Område i en triangel

Formeln för att beräkna ytan för vilken triangel som helst är A = (b × h) / 2, där “b” är längden på basen och “h” är längden på höjden.

- Vinklar av en triangel

Summan av de tre inre vinklarna i en triangel är 180º.

- Trigonometriska funktioner:

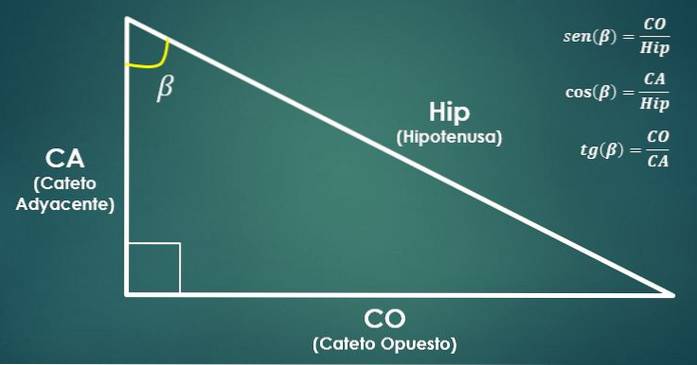
Tänk på en rätt triangel. Därefter definieras de trigonometriska funktionerna sinus, cosinus och tangent för vinkeln beta (β) enligt följande:

sin (β) = CO / Hip, cos (β) = CA / Hip and tan (β) = CO / CA.

Hur man hittar sidorna och vinklarna i en rätt triangel?

Med tanke på en rätt triangel ABC kan följande situationer uppstå:

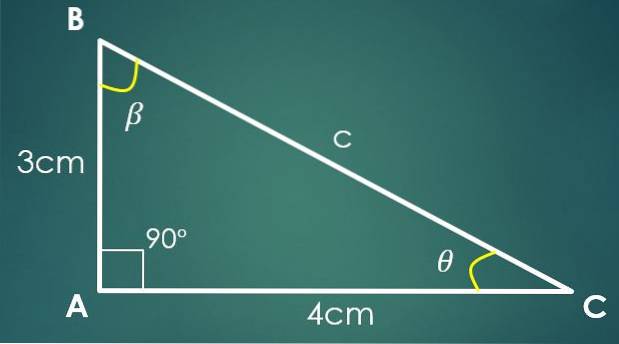
1- De två benen är kända

Om benet “a” mäter 3 cm och benet “b” mäter 4 cm, används den pythagoreiska satsen för att beräkna värdet på “c”. Genom att ersätta värdena "a" och "b" får vi att c² = 25 cm², vilket innebär att c = 5 cm.

Om vinkeln β är mittemot benet “b”, är sin (β) = 4/5. Genom att tillämpa sinusens inversa funktion, i denna sista jämställdhet får vi att β = 53,13º. Två inre vinklar i triangeln är redan kända.

Låt θ vara den vinkel som återstår att känna, sedan 90º + 53,13º + θ = 180º, varifrån vi får att θ = 36,87º.

I det här fallet är det inte nödvändigt att de kända sidorna är de två benen, det viktiga är att känna till värdet av två sidor.

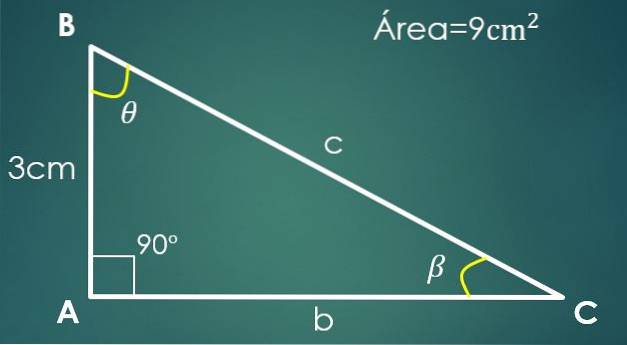
2- Ett ben är känt och området

Låt a = 3 cm vara det kända benet och A = 9 cm² triangelns yta.

I en rätt triangel kan ett ben betraktas som bas och det andra som höjd (eftersom de är vinkelräta).

Antag att "a" är basen, därför 9 = (3 × h) / 2, varifrån vi får att det andra benet är 6 cm. För att beräkna hyposenus, fortsätt som i föregående fall, och vi får att c = √45 cm.

Om vinkeln β är mittemot benet “a”, är sin (β) = 3 / √45. Lösning för β erhålls att dess värde är 26,57º. Vi behöver bara veta värdet på den tredje vinkeln θ.

Man är övertygad om att 90º + 26,57º + θ = 180º, varifrån man drar slutsatsen att θ = 63,43º.

3- En vinkel och ett ben är kända

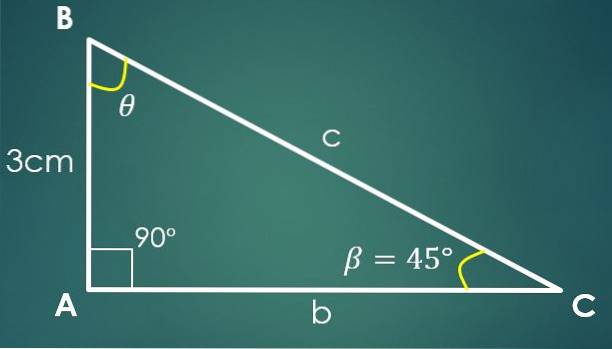
Låt β = 45º vara den kända vinkeln och a = 3 cm det kända benet, där benet “a” är motsatt vinkeln β. Med tangentformeln får vi att tg (45º) = 3 / CA, varifrån det följer att CA = 3 cm.

Med användning av Pythagoras sats erhålls att c² = 18 cm², det vill säga c = 3√2 cm.

Det är känt att en vinkel mäter 90º och att β mäter 45º, härav dras slutsatsen att den tredje vinkeln mäter 45º.

I det här fallet behöver den kända sidan inte vara ett ben, det kan vara någon av de tre sidorna av triangeln.

Referenser

1. Landaverde, F. d. (1997). Geometri (Omtryck ed.). Framsteg.
2. Leake, D. (2006). Trianglar (illustrerad utgåva). Heinemann-Raintree.
3. Pérez, C. D. (2006). Förberäkning. Pearson Education.
4. Ruiz, Á., & Barrantes, H. (2006). Geometrier. CR-teknik.
5. Sullivan, M. (1997). Förberäkning. Pearson Education.
6. Sullivan, M. (1997). Trigonometri och analytisk geometri. Pearson Education.