De determinationskoefficient är ett tal mellan 0 och 1 som representerar bråkdelen av punkter (X, Y) som följer regressionspassningslinjen för en datamängd med två variabler.
Det är också känt som godhet av passform och betecknas med Rtvå. För att beräkna det tas kvoten mellan variansen för data Ŷi uppskattad av regressionsmodellen och variansen för data Yi som motsvarar varje Xi av data.
Rtvå = Sŷ / Sy
Om 100% av data är på linjen för regressionsfunktionen, kommer bestämningskoefficienten att vara 1.
Tvärtom, om för en uppsättning data och en viss justeringsfunktion koefficienten Rtvå visar sig vara lika med 0,5, då kan man säga att passformen är 50% tillfredsställande eller bra.
På samma sätt, när regressionsmodellen returnerar värden på Rtvå lägre än 0,5, indikerar detta att den valda justeringsfunktionen inte anpassas tillfredsställande till data, därför är det nödvändigt att leta efter en annan justeringsfunktion.
Och när kovarians eller den korrelationskoefficient tenderar att vara noll, då är variablerna X och Y i data orelaterade och därför Rtvå tenderar också att vara noll.
Artikelindex
I föregående avsnitt sa man att bestämningskoefficienten beräknades genom att hitta kvoten mellan varianserna:
-Uppskattad av regressionsfunktionen för variabeln Y
-Den för variabeln Yi som motsvarar var och en av variablerna Xi för N-dataparen.
Angivet matematiskt ser det ut så här:
Rtvå = S / Sy
Av denna formel följer att Rtvå representerar variansandelen förklarad av regressionsmodellen. Alternativt kan R beräknastvå med hjälp av följande formel, helt ekvivalent med den föregående:
Rtvå = 1 - (Sε / Sy)
Där Sε representerar variansen för resterna εi = Ŷi - Yi, medan Sy är variansen för uppsättningen Yi-värden för datan. För att bestämma Ŷi används regressionsfunktionen, vilket innebär att bekräfta att Ŷi = f (Xi).
Variansen för datamängden Yi, med i från 1 till N beräknas enligt följande:
Sy = [Σ (Yi -
Och fortsätt sedan på ett liknande sätt för Sŷ eller för Sε.
För att visa detaljerna i hur beräkningen av determinationskoefficient vi tar följande uppsättning med fyra datapar:
(X, Y): (1, 1); (2. 3); (3, 6) och (4, 7).
En linjär regressionspassning föreslås för denna datamängd, som erhålls med metoden med minsta kvadrat:
f (x) = 2,1 x - 1
Genom att använda denna justeringsfunktion erhålls vridmomenten:
(X, Ŷ): (1, 1.1); (2, 3,2); (3, 5.3) och (4, 7.4).
Sedan beräknar vi det aritmetiska medelvärdet för X och Y:
Varians Sy
Sy = [(1 - 4,25)två + (3 - 4,25)två + (6 - 4,25)två +….…. (7 - 4.25)två] / (4-1) =
= [(-3,25)två+ (-1,25)två + (1,75)två + (2,75)två) / (3)] = 7.583
Varians Sŷ
S2 = [(1,1 - 4,25)två + (3,2 - 4,25)två + (5.3 - 4.25)två +….…. (7.4 - 4.25)två] / (4-1) =
= [(-3,25)två + (-1,25)två + (1,75)två + (2,75)två) / (3)] = 7,35
Bestämningskoefficient Rtvå
Rtvå = S2 / Sy = 7,35 / 7,58 = 0,97
Bestämningskoefficienten för det illustrativa fallet som beaktades i föregående segment visade sig vara 0,98. Med andra ord, den linjära justeringen genom funktionen:
f (x) = 2,1 x - 1
Det är 98% tillförlitligt när det gäller att förklara de data som det erhölls med metoden med minst kvadrat..
Förutom bestämningskoefficienten finns det linjär korrelationskoefficient eller även känd som Pearsons koefficient. Denna koefficient, betecknad som r, beräknas av följande förhållande:
r = Sxy / (Sx Sy)
Här representerar täljaren kovariansen mellan variablerna X och Y, medan nämnaren är produkten av standardavvikelsen för variabeln X och standardavvikelsen för variabeln Y.
Pearsons koefficient kan ta värden mellan -1 och +1. När denna koefficient tenderar att +1 finns en direkt linjär korrelation mellan X och Y. Om den tenderar till -1 istället finns det en linjär korrelation men när X ökar minskar Y. Slutligen är det nära 0, det finns ingen korrelation mellan de två variablerna.
Det bör noteras att bestämningskoefficienten sammanfaller med fyrkanten för Pearson-koefficienten, endast när den första har beräknats baserat på en linjär passning, men denna jämlikhet gäller inte för andra icke-linjära kopplingar..
En grupp gymnasieelever bestämde sig för att bestämma en empirisk lag för pendeltiden som en funktion av dess längd. För att uppnå detta mål utför de en serie mätningar där de mäter tiden för en pendelsvängning för olika längder och uppnår följande värden:
| Längd (m) | Period (er) |
|---|---|
| 0,1 | 0,6 |
| 0,4 | 1.31 |
| 0,7 | 1,78 |
| 1 | 1,93 |
| 1.3 | 2.19 |
| 1.6 | 2,66 |
| 1.9 | 2,77 |
| 3 | 3,62 |
Det uppmanas att göra en spridningsdiagram av data och utföra en linjär passning genom regression. Visa också regressionsekvationen och dess bestämningskoefficient.
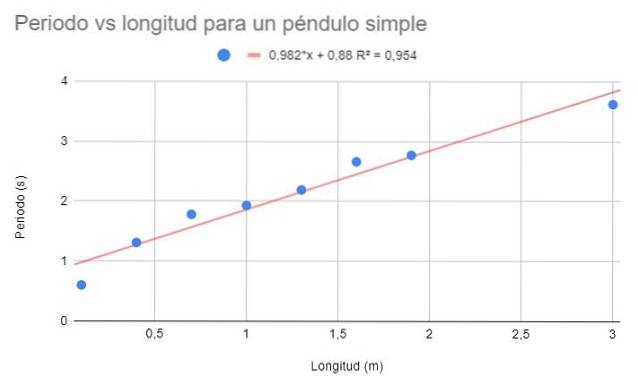
En ganska hög bestämningskoefficient kan observeras (95%), så man kan tro att linjär passform är optimal. Men om punkterna ses tillsammans verkar det som om de har en tendens att kurva nedåt. Denna detalj beaktas inte i den linjära modellen.
För samma data i exempel 1, skapa en spridningsdiagram över data. Vid detta tillfälle, till skillnad från exempel 1, begärs en regressionsjustering med en potentiell funktion.
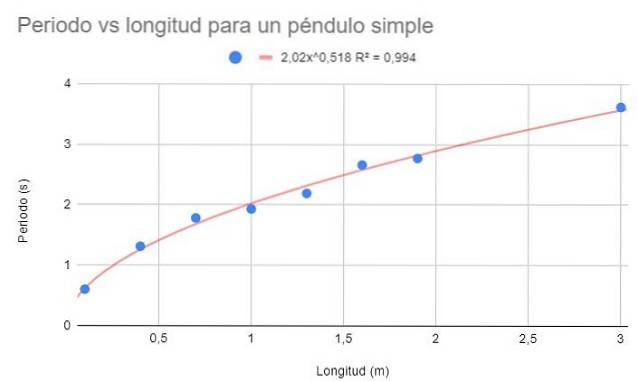
Visa även anpassningsfunktionen och dess bestämningskoefficient Rtvå.
Den potentiella funktionen är av formen f (x) = AxB, där A och B är konstanter som bestäms av metoden för minsta kvadrat.
Den föregående figuren visar den potentiella funktionen och dess parametrar, samt bestämningskoefficienten med ett mycket högt värde på 99%. Observera att data följer kurvans trendlinje.
Använd samma data från exempel 1 och exempel 2 och utför en andra graders polynompassning. Visa graf, polynom av passform och bestämningskoefficient Rtvå korrespondent.
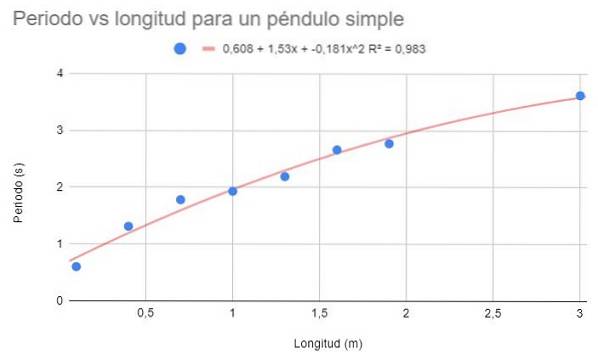
Med andra gradens polynompassning kan du se en trendlinje som passar väl krökningen av datan. Bestämningskoefficienten ligger också över den linjära passningen och under den potentiella passningen..
Av de tre passningarna som visas är den som har den högsta bestämningskoefficienten den potentiella passningen (exempel 2).
Den potentiella passningen sammanfaller med den fysiska teorin för pendeln, som, som känt, fastställer att pendelns period är proportionell mot kvadratroten av dess längd, varvid proportionalitetskonstanten är 2π / √g där g är accelerationen av allvar.
Denna typ av potentialanpassning har inte bara den högsta bestämningskoefficienten utan exponenten och proportionalitetskonstanten matchar den fysiska modellen..
-Regressionspassning bestämmer parametrarna för funktionen som är avsedd att förklara data med hjälp av metoden med minsta kvadrat. Denna metod består i att minimera summan av den kvadratiska skillnaden mellan Y-värdet för justering och Yi-värdet för data för Xi-värdena för datan. Detta bestämmer parametrarna för justeringsfunktionen.
-Som vi har sett är den vanligaste justeringsfunktionen linjen, men den är inte den enda, eftersom justeringarna också kan vara polynomiska, potentiella, exponentiella, logaritmiska och andra..
-I vilket fall som helst beror bestämningskoefficienten på data och typ av passform och är en indikation på godheten hos den passform som tillämpas..
-Slutligen indikerar bestämningskoefficienten den procentuella totala variabiliteten mellan Y-värdet för datan med avseende på Ŷ-värdet för passningen för den angivna X.
Ingen har kommenterat den här artikeln än.