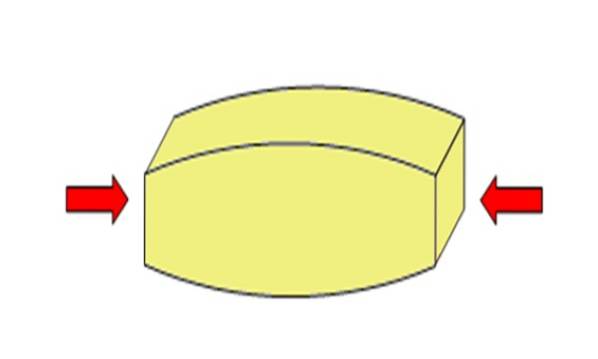
De kompression eller kompressionsspänning är kraften per ytenhet vars resultat är att skjuta, klämma eller komprimera ett föremål och tenderar att förkorta det. Matematiskt är det:
E = F / A
Här OCH betecknar ansträngning, F storleken på kraften och TILL det område som det agerar på, enheten i SI International System är newton / mtvå eller pascal (Pa). Kompressiv stress är en normal ansträngning, eftersom den kraft som producerar den är vinkelrät mot det område som den utövas på.
En sådan ansträngning kan komprimera objektet eller tvärtom spänna och sträcka det, när det tillämpas. Vid tryckspänning appliceras krafterna i motsatt riktning för att utöva effekten av att klämma och förkorta objektet.
När krafterna upphör återgår många material till sina ursprungliga dimensioner. Den här egenskapen är känd under namnet elasticitet. Men medan det händer är den elastiska enhetsdeformationen som drabbas av ett material som utsätts för en spänning:
Stam = (slutlig storlek - ursprunglig storlek) / ursprunglig storlek
Töjningen kan vara linjär, ytlig eller volymetrisk, även om töjningen är enhetlös. Informationen den ger är dock mycket viktig, eftersom det inte är detsamma att deformera en 10 m lång stång med 1 cm, att deformera ytterligare 1 m lång stång med 1 cm.
I ett elastiskt material är deformation och spänning proportionell och uppfyller Hookes lag:
Ansträngning ∝ Enhetens deformation
Artikelindex
Kompressionsspänningen får partiklarna i materialet att komma närmare och närmare, vilket minskar deras storlek. Beroende på i vilken riktning ansträngningen appliceras kommer vissa av dess dimensioner att förkortas eller minskas.
Låt oss börja med att anta en tunn stapel med originallängd L, till vilken normal spänning av storlek OCH. Om spänningen är komprimerande upplever stången en minskning av dess längd, betecknad med 5. Om det är spänning kommer stången att förlängas.
Naturligtvis är materialet av vilket elementet är tillverkat avgörande för dess förmåga att motstå stress..
Dessa elastiska egenskaper hos materialet ingår i den ovannämnda proportionalitetskonstanten. Heter elasticitetsmodul eller Youngs modul och betecknas Y. Varje material har en elasticitetsmodul, som bestäms experimentellt genom laboratorietester.
Med detta i åtanke, ansträngningen OCH Det uttrycks i matematisk form så här:
Ansträngning ∝ Enhetens deformation
Slutligen, för att fastställa detta villkor som en ekvation, krävs en konstant proportionalitet för att ersätta symbolen för proportionalitet ∝ och ersätta den för jämlikhet, så här:
Stress = proportionalitetskonstant x enhetsbelastning
E = Y. (5 / L)
Kvoten (5 / L) är stammen, betecknad som ε och med 5 = Slutlig längd - Initial längd. På detta sätt ansträngningen OCH ser ut som:
E = Y. ε
Eftersom töjningen är dimensionell, är enheterna i Y är samma som de av OCH: N / mtvå o Pa i SI-systemet, pounds / intvå eller psi i det brittiska systemet, liksom andra kombinationer av kraft och area, såsom kg / cmtvå.
Y-värden bestäms experimentellt i laboratoriet under kontrollerade förhållanden. Därefter är elasticitetsmodulen för material som används i stor utsträckning i konstruktionen och även för ben:
bord 1
| Material | Elasticitetsmodul Y (Pa) x 109 |
|---|---|
| Stål | 200 |
| Järn | 100 |
| Mässing | 100 |
| Brons | 90 |
| Aluminium | 70 |
| Marmor | femtio |
| Granit | Fyra fem |
| Betong | tjugo |
| Ben | femton |
| Tall | 10 |
Kompressionskrafter verkar på olika strukturer; De är föremål för påverkan av krafter som vikten på vart och ett av elementen som komponerar dem, liksom krafter från yttre agenser: vind, snö, andra strukturer och mer..
Det är vanligt att de flesta strukturer är utformade för att tåla påkänningar av alla slag utan att deformeras. Därför måste kompressionsspänningen tas med i beräkningen för att förhindra att delen eller föremålet förlorar sin form..
Skelettets ben är också strukturer som utsätts för olika påfrestningar. Även om benen är motståndskraftiga mot dem, uppstår sprickor och sprickor när de av en slump överskrids.
Byggkolonner och bryggor måste göras för att motstå kompression, annars tenderar de att böjas. Detta kallas lateral böjning eller knäckning.
Kolumnerna (se figur 1) är element vars längd är betydligt större jämfört med tvärsnittsarean..
Ett cylindriskt element är en kolonn när dess längd är lika med eller större än tio gånger tvärsektionens diameter. Men om tvärsnittet inte är konstant kommer dess mindre diameter att tas för att klassificera elementet som en kolumn.
När människor sätter sig på möbler som stolar och bänkar eller lägger till föremål ovanpå utsätts benen för kompressionsspänningar som tenderar att minska höjden..
Möbler är vanligtvis gjorda för att motstå vikt ganska bra och återgår till sitt naturliga tillstånd när de har tagits bort. Men om tung vikt läggs på ömtåliga stolar eller bänkar, ger benen plats för kompression och brott..
Det finns en stång som ursprungligen mäter 12 m i längd, som den utsätts för en kompressionsspänning så att dess enhetsdeformation är -0.0004. Vad är stångens nya längd?
Med utgångspunkt från ekvationen ovan:
ε = (5 / L) = - 0,0004
Ja LF är den slutliga längden och Leller den ursprungliga längden, sedan 5 = LF - Leller du har:
(LF - Leller) / L.eller = -0.0004
Därför: LF - Leller = -0.0004 x 12 m = -0.0048 m. Och slutligen:
LF = (12 - 0,0048) m = 11,9952 m.
En solid stålstång, cylindrisk i form, är 6 m lång och 8 cm i diameter. Om stången komprimeras med en belastning på 90 000 kg, hitta:
a) Storleken på kompressionsspänningen i megapascal (MPa)
b) Hur mycket minskade stapelns längd?
Först hittar vi området A för stångens tvärsnitt, vilket beror på dess diameter D, vilket resulterar i:
A = π. Dtvå / 4 = π. (0,08 m)två / 4 = 5,03 x 10-3 mtvå
Kraften hittas omedelbart igenom F = m.g = 90 000 kg x 9,8 m / stvå= 882 000 N..
Slutligen beräknas den genomsnittliga insatsen så här:
E = F / A = 882 000 N / 5,03 x 10-3 mtvå = 1,75 x 108 Pa = 175 MPa
Nu används ekvationen för stress, med vetskap om att materialet har ett elastiskt svar:
E = Y. (5 / L)
Youngs modul av stål återfinns i tabell 1:
5 = E.L / Y = 6 m x 1,75 x 108 Pa / 200 x 10 9 Pa = 5,25 x 10 -3 m = 5,25 mm.
Ingen har kommenterat den här artikeln än.