Bevarande av linjär momentumprincip, exempel, övningar.

De bevarande av linjär fart av en kropp fastställer att produkten av dess massa och dess hastighetsvektor är en konstant mängd, när kroppen är fri från interaktion med andra kroppar och med den uppmätta hastigheten med avseende på en fast eller icke-accelererad referensram.

När du har flera kroppar som bara interagerar med varandra, men inte med den yttre miljön, då linjär fart av uppsättningen förblir också konstant över tiden.

Linjär momentum, momentum eller helt enkelt Momentum, betecknas med bokstaven sid y är en vektormängd:

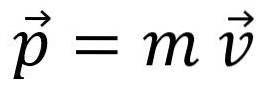
Momentum är inte samma som hastighet, även om förhållandet är uppenbart: till exempel, en lastbil som går 20 km / h har mer fart än en cykel som rör sig i samma hastighet.

För att en kropps linjära momentum ska förändras måste en extern extern kraft verka på den, annars förblir den konstant. Också det linjära ögonblicket P av ett system bildat av n-kroppar är vektorsumman för de enskilda ögonblicken:

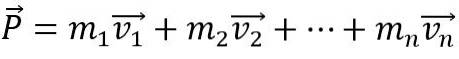
Artikelindex

• 1 Princip för bevarande av linjär momentum
• 2 Exempel
  • 2.1 Exempel 1
  • 2.2 Exempel 2
  • 2.3 Exempel 3
• 3 applikationer
  • 3.1 Sänd i rymden
  • 3.2 Dagligt liv
• 4 Övningar
  • 4.1 Övning 1
  • 4.2 Övning 2
• 5 Referenser

Princip för bevarande av linjär momentum

I en kraftfri kropp (eller i vilken alla krafter på den avbryts) händer det att det linjära momentet förblir konstant.

Detsamma händer i ett system som bildas av flera kroppar som bara interagerar med varandra, men inte med den yttre miljön: systemets totala linjära momentum förblir fast under utvecklingen av helhetens rörelse..

Denna bevarande princip anges enligt följande:

Den totala drivkraften för en uppsättning n-kroppar som bara interagerar med varandra, men inte med den yttre miljön, är en oföränderlig kvantitet i tiden.

Och matematiskt uttrycks det enligt följande:

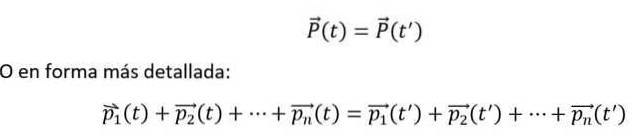
Ovanstående likheter uppfylls, om och bara om n-kroppar interagerar med varandra, men inte med den yttre miljön. Dessutom måste enskilda moment alltid mätas i förhållande till en tröghetsreferensram..

Exempel

Exempel 1

Två astronauter i rymden håller hand och hålls i en fast position relativt rymdfarkosten. Men om de skjuter varandra börjar de separera i motsatta riktningar, sett från fartyget..

I det här fallet, eftersom interaktionen mellan astronauterna endast sker mellan dem genom deras kontaktkraft, är det totala momentet efter tryckning fortfarande det initiala värdet med avseende på rymdfarkosten. Det vill säga total momentum 0.

Emellertid förändrades varje astronauts fart. Ursprungligen hade var och en 0 linjärt ögonblick i förhållande till fartyget, men efter att ha skjutits ut går en i en riktning och den andra i motsatt riktning, med linjära moment som inte är noll lika stora och motsatta riktningar..

Således, när de enskilda momenten adderas vektorellt, erhålls det initiala totala momentum som ett resultat, vilket är noll.

Å andra sidan indikerar bevarande av momentumkvantiteten att astronauten med den lägsta massan är den som rör sig snabbare i förhållande till rymdfarkosten. Men resultatet av att multiplicera dess massa med dess hastighet är lika med den produkt som erhålls genom att multiplicera den andras massa med den andras hastighet.

Exempel 2

En valp är på en flytande plattform i en lugn sjö och hans ägare bevakar honom från en brygga. I början vilar både plattformen och valpen, men när valpen vill komma närmare ägaren rör sig plattformen bort från bryggan.

Förklaringen till denna observation ligger just i principen för bevarande av mängden linjärt momentum. Systemet består av valpen och plattformen.

Valpen kan gå på plattformen tack vare friktionskraften mellan benen och ytan, i det här fallet är friktionskraften en intern interaktionskraft mellan den och plattformen.

Helheten är ett isolerat system, eftersom plattformen kan röra sig horisontellt över sjön, fri från motstånd mot rörelse. Å andra sidan, i vertikal riktning är alla krafter balanserade och kompenserade, och helheten har ingen rörelse i den riktningen..

Därför uppfylls alla hypoteser i denna situation så att principen för bevarande av linjär momentum gäller.

Exempel 3

En eskimo är fångad i mitten av en frusen sjö, isen är så slät att oavsett hur hårt han försöker, glider eskimo och stannar alltid på samma plats.

Det enda möjliga sättet för Eskimo att komma ut ur sjön är att han kastar i motsatt riktning som han vill flytta ett tungt föremål som han bär i sin ryggsäck (förutsatt att han bär en).

Applikationer

Sänd i rymden

Bevarande av linjär momentum appliceras för att driva en raket in i rymden där det inte finns några yttre krafter. I detta fall uppnås fartygets impuls genom att utvisa gaser i hög hastighet så att raketen kan röra sig i motsatt riktning som de kastades ut med..

Om fartyget ursprungligen ligger i vila, när det bränner och driver ut bränsle, sker utdrivningskraften mot själva fartyget. Det är en inre kraft mellan gaserna och fartyget. Det finns inga externa krafter och därför gäller bevarande av linjär momentum.

Eftersom gasernas linjära momentum är densamma och motsatt fartygets, lyckas det komma ur vila och genom att fortsätta att utvisa gaser ökar det sin rörelsemängd och därmed dess hastighet.

Dagligt liv

Ett annat fall av tillämpning av bevarande av linjär momentum i vardagen är att driva en spik i träet och utnyttja hammarens rörelse eller momentum..

Det kan hävdas att i detta fall inte principen gäller, eftersom det finns en yttre kraft: motståndet som träet erbjuder mot spiken..

I kontaktögonblicket är dock kraften som hammaren påför spiken en inre kraft (mellan systemet som är spiken och hammaren) mycket större än motståndet som träet motsätter sig, och därför är den senare försumbar.

Hela hammarens drivkraft, som är ganska stor på grund av sin stora massa och hastighet, överförs till spiken strax efter kollisionen. Observera att hela ögonblicket, men inte hela hammarens kinetiska energi, överförs, eftersom en del av detta omvandlas till termisk energi i spiken och i hammaren, vilket höjer temperaturen efter stöten.

Träning

Övning 1

Astronauterna Andrew och Berenice är utanför rymdstationen och håller båda händerna och vilar relativt stationen. De drivs genom att skjuta händerna på den ena mot den andra och de släpps. Om Andrew, 70 kg massa, rör sig vid 1 m / s i förhållande till stationen, vad är hastigheten för Berenice med 49 kg massa?

Lösning

I detta fall gäller hypoteserna om bevarande av linjär momentum tydligt, eftersom det inte finns några yttre krafter i yttre rymden. Kraften med vilken båda astronauterna trycker på sina händer är en inre kraft.

Antag att Andrews massa är M_till och Berenice M._b. På samma sätt är hastigheterna för båda efter impulsen V_till för Andrew och V_b för Berenice. Då gäller bevarande av linjär momentum så här:

M_till∙0 + M_b∙0 = M_till∙V_till+ M_b∙V_b

Lösning för Berenices hastighet har vi:

V_b = - (M_till / M_b) ∙ V_till

Placera de numeriska värdena:

V_b = - (70/49) ∙ (1m / s) eller = -1,43m / s eller

Det vill säga, Berenice rör sig med en hastighet på 1,43 m / s i motsatt riktning till Andrews.

Övning 2

En valp med en massa på 5 kg vilar på en 15 kg plattform som flyter, även i vila, på en still sjö. Om valpen börjar gå på plattformen med en hastighet på 0,5 m / s i förhållande till den. Hur snabbt kommer valpen och plattformen att ha i förhållande till en observatör som är fixerad i marken??

Lösning

Tröghetsreferenssystemet tas som bryggan där valpens ägare befinner sig. Inledningsvis vilar både valpen och den flytande plattformen i förhållande till bryggan..

När valpen bestämmer sig för att snabbt gå mot ägaren v ' relativt plattformen rör sig plattformen bort från piren med hastighet +V. Valpens hastighet med avseende på fjädern erhålls med vektorsumman av dess hastighet i förhållande till plattformen plus plattformens hastighet och vi betecknar den med:

v = -v'' + V

Eftersom vattnets motstånd mot plattformens rörelse praktiskt taget är noll på grund av dess låga hastighet, kan det konstateras att systemet består av valpen + plattformen är ett isolerat system och principen för bevarande av linjär momentum gäller:

0 = m ∙ v + M ∙ V

Att komma ihåg att v = v '+ V har vi:

0 = -m ∙ v '+ m ∙ v + M ∙ V

Det vill säga: m ∙ v '= (m + M) ∙ V

Därför V = [m / (m + M)] v 'och v = - (M / m) V = - [M / (m + M)] v'

Att ersätta de numeriska värdena vi har:

V = [5 / (5 +15)] ∙ 0,5 m / s = 0,125 m / s

Detta är den hastighet med vilken plattformen rör sig från bryggan.

V = - (15/20) ∙ 0,5m / s = -0,375 m / s

Och detta är den hastighet med vilken valpen närmar sig kajen.

Referenser

1. Duke University. System av partiklar. Återställd från: webhome.phy.duke.edu.
2. Rex, A. 2011. Grundläggande fysik. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Red. Volym 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7: e. Ed. Cengage Learning.
5. .