
Enhetscirkel trigonometriska funktioner och applikationer
De enhetscirkel är en cirkel med radie lika med 1, som vanligtvis är centrerad vid punkten (0,0) i det kartesiska koordinatsystemet xy. Används för att enkelt definiera trigonometriska förhållanden för vinklar med hjälp av rätt trianglar.
Ekvationen för enhetscirkeln centrerad vid ursprunget är:
xtvå + Ytvå = 1
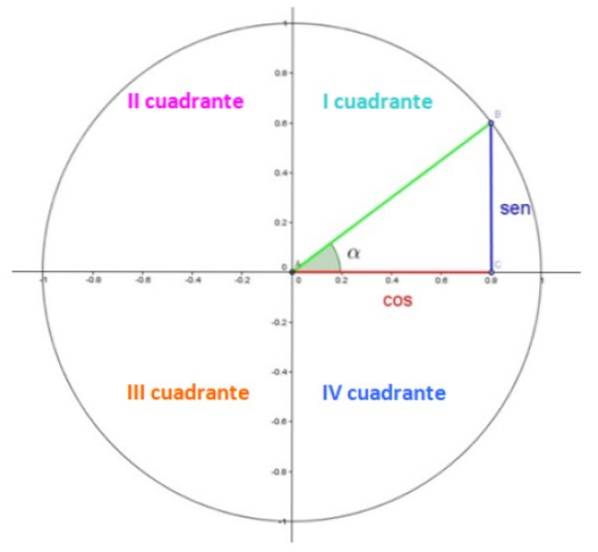
I figur 1 har vi enhetscirkeln, där varje kvartal är i en kvadrant. Kvadranter är numrerade med romerska siffror och räknas moturs.
I den första kvadranten finns en triangel. Benen, i rött och blått, mäter 0,8 respektive 0,6, medan hypotenusen i grönt mäter 1, eftersom det är en radie.
Den spetsiga vinkeln α är en central vinkel i standardläge, vilket innebär att dess toppunkt sammanfaller med punkten (0,0) och dess initiala sida med den positiva x-axeln. Vinkeln mäts moturs och tilldelas ett positivt tecken enligt konvention.
Tja, i enhetscirkeln är cosinus- och sinuskoordinaterna för α respektive x- och y-koordinaterna för punkt B, som i exemplet som visas är 0,8 och 0,6.
Från dessa två definieras de:
- tg a = sin a / cos a = 0,6 / 0,8 = 0,75
- sek a = 1 / cos a = 1 / 0,8 = 1,25
- cosec α = 1 / sin α = 1 / 0.6 = 1.66…
- ctg α = 1 / tg = 0,8 / 0,6 = 1,33 ...
Artikelindex
- 1 applikationer för enhetscirkel
- 1.1 Referensvinkel
- 2 Rita graferna för cosinus och sinus
- 2.1 Egenskaper hos sinus- och cosinusfunktioner
- 3 Lösta övningar
- 3.1 - Övning 1
- 3.2 - Övning 2
- 4 Referenser
Enhetscirkelapplikationer
Om vi begränsar oss till rätt trianglar, skulle de trigonometriska förhållandena endast gälla akuta vinklar. Men med hjälp av enhetscirkeln utvidgas beräkningen av trigonometriska förhållanden till vilken vinkel som helst.
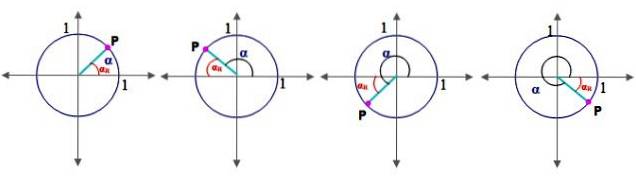
För detta är det nödvändigt att först definiera begreppet referensvinkel aR:
Referensvinkel
Låt α vara en vinkel i standardläge (den vars startsidan sammanfaller med den positiva x-axeln), dess referensvinkel αR är mellan hans terminalsidan och x-axeln. Figur 2 visar referensvinkeln för vinklar i I, II, III och IV kvadranten.
För varje kvadrant beräknas referensvinkeln så här:
-Första kvadranten: αR = α
-Andra kvadranten: αR = 180º - α
-Tredje kvadranten: αR = α - 180º
-Fjärde kvadranten: αR = 360º - α
Observera att den första kvadranten vinkeln α sammanfaller med dess referensvinkel. Tja, de trigonometriska förhållandena för vinkeln α är desamma som deras referensvinkel, med tecknen enligt de kvadranter i vilka terminalens sida av α faller..
Med andra ord sammanfaller trigonometriska cosinus- och sinusförhållandena för vinkeln a med koordinaterna för punkten P, enligt figur 2.
I följande figur ser vi de trigonometriska förhållandena för vissa anmärkningsvärda vinklar, som härleds från enhetscirkeln.
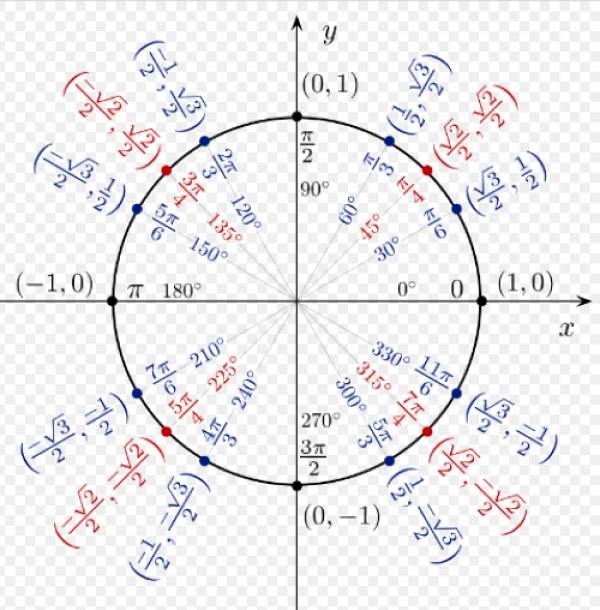
Förhållandena mellan cosinus och sinus för alla vinklar i I-kvadranten är alla positiva. För α = 60º har vi koordinaterna (1/2; √3 / 2), som motsvarar cos 60º respektive sin 60º.
Koordinaterna för α = 120º är (-1/2; √3 / 2), eftersom de är i den andra kvadranten är x-koordinaten negativ.
Plottning av cosinus- och sinusdiagram
Med hjälp av enhetscirkeln och koordinaterna för punkterna P på den är det möjligt att rita graferna för funktionerna cos t och sin t, som vi kommer att se nedan.
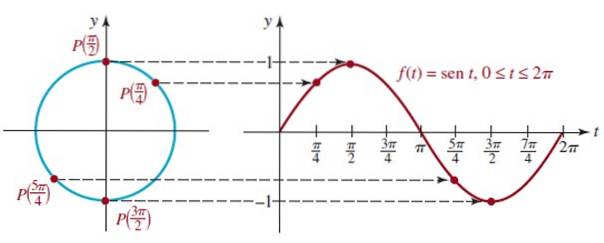
För att göra detta finns olika positioner för punkten P (t) på enhetscirkeln. Vi börjar med grafen för funktionen f (t) = sin t.
Vi kan se att när vi går från t = 0 till t = π / 2 (90º) ökar värdet på sin t tills det når 1, vilket är det maximala värdet.
Å andra sidan, från t = π / 2 till t = 3π / 2 minskar värdet på sin t från 1 och passerar genom 0 vid t = π tills det når sitt minimum -1 vid t = 3π / 2.
Figuren visar diagrammet för den första cykeln av f (t) = sin t som motsvarar den första omgången av enhetscirkeln, denna funktion är periodisk med period 2π.
En analog procedur kan utföras för att erhålla grafen för funktionen f (t) = cos t, som visas i följande animation:
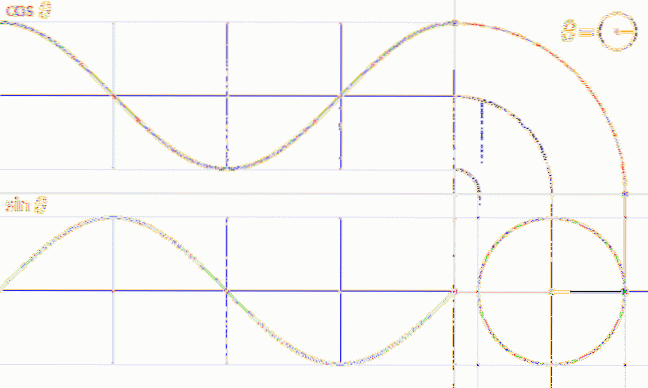
Egenskaper hos sinus- och cosinusfunktioner
-Båda funktionerna är kontinuerliga i uppsättningen av reella tal och även periodiska av period 2π.
-Funktionens domän f (t) = sin t och f (t) = cos t är alla reella tal: (-∞, ∞).
-För intervallet eller banan för sinus och cosinus har vi intervallet [-1,1]. Parenteserna indikerar att -1 och 1 ingår.
- Nollorna till sin t är de värden som motsvarar nπ med n heltal, medan nollorna för cos t är [(2n + 1) / 2] med n också heltal.
-Funktionen f (t) = sin t är udda, den har symmetri om ursprunget medan funktionen cos t är jämn, dess symmetri handlar om den vertikala axeln.
Lösta övningar
- Övning 1
Med tanke på cos t = - 2/5, vilket är den horisontella koordinaten för punkten P (t) på enhetscirkeln i den andra kvadranten, erhåll motsvarande vertikal koordinat sin t.
Lösning
Eftersom P (t) tillhör enhetscirkeln, där det är sant att:
xtvå + Ytvå = 1
Därför:
y = ± √ 1 - xtvå
Eftersom P (t) ligger i andra kvadranten kommer det positiva värdet att tas. Den vertikala koordinaten för punkten P (t) är y:
y = √ 1 - (-2/5)två = √0,84
- Övning 2
En matematisk modell för temperatur T i grader Fahrenheit på en viss dag, t timmar efter midnatt ges det av:
T (t) = 50 + 10 sin [(π / 12) × (t - 8)]
Med t mellan 0 och 24 timmar. Hitta:
a) Temperaturen klockan 8.
b) Timmar under vilka T (t) = 60ºF
c) Högsta och lägsta temperatur.
Lösning till
Vi ersätter t = 8 i den givna funktionen:
T (8) = 50 + 10 sin [(π / 12) × (t-8)] = 50 + 10 sin [(π / 12) × (8-8)] =
= 50 + 10 x sin 0 = 50 ºF
Lösning b
50 + 10 sin [(π / 12) × (t-8)] = 60
Det är en trigonometrisk ekvation och vi måste lösa det okända "t":
10 sin [(π / 12) × (t-8)] = 60 - 50 = 10
sin [(π / 12) × (t-8)] = 1
Vi vet att sin π / 2 = 1, därför måste sinusargumentet vara 1:
(π / 12) × (t-8) = π / 2
t-8 = 6
t = 14 timmar
Slutsatsen är att vid 14 timmar efter midnatt är temperaturen 60º, det vill säga 14.00. Det finns ingen annan tid hela dagen (24 timmar) när detta händer.
Lösning c
Den maximala temperaturen motsvarar det värde vid vilket sin [(π / 12) × (t-8)] = 1 och är 60 ºF. Å andra sidan inträffar minimum om sin [(π / 12) × (t-8)] = -1 och är 40ºF.
Referenser
- Figuera, J. 1999. Matematik. 1: a Diversifierad. Bolivarian Collegiate Editions.
- Hoffman, J. Selection of Mathematics Topics. Volym 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematik är kul, enhetscirkel. Återställd från: de: mathsisfun.com.
- Wikipedia. Trigonometriidentiteter och formler. Återställd från: es.wikipedia.org.
- Zill, D. 1984. Algebra och trigonometri. Mcgraw hill.


Ingen har kommenterat den här artikeln än.