
Fyrsidiga element, egenskaper, klassificering, exempel
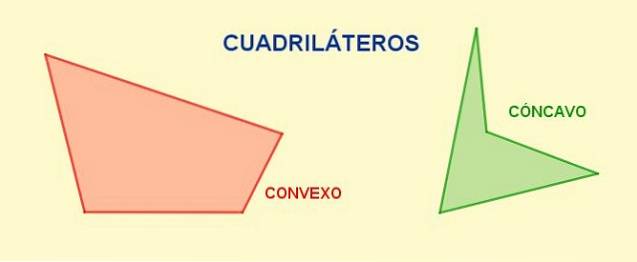
A fyrsidig är en polygon med fyra sidor och fyra hörn. Deras motsatta sidor är de som inte har gemensamma hörn, medan de är på varandra följande sidor de med ett gemensamt toppunkt.
I en fyrkant är de intilliggande vinklar de som delar en sida, medan motsatta vinklar de har inga sidor gemensamt. En annan viktig egenskap hos en fyrkant är att summan av dess fyra inre vinklar är två gånger planvinkeln, det vill säga 360 ° eller 2π radianer.
Diagonaler är segmenten som sammanfogar ett toppunkt med dess motsats och i en given fyrkant kan från varje toppunkt dras en enda diagonal. Det totala antalet diagonaler i en fyrkant är två.
Fyrkantiga figurer är figurer som är kända för mänskligheten sedan urminnes tider. De arkeologiska uppgifterna, liksom de konstruktioner som överlever idag, intygar detta..
På samma sätt fortsätter fyrkantarna i dag att ha en viktig närvaro i allas dagliga liv. Läsaren kan hitta denna form på skärmen där texten läses just nu, på fönster, dörrar, bildelar och otaliga andra platser..
Artikelindex
- 1 Klassificering av fyrhjulingar
- 1.1 Typer av parallellogram
- 2 Trapes
- 2.1 Typer av trapets
- 3 Parallelogram
- 3.1 Område för ett parallellogram
- 3.2 Diagonaler av ett parallellogram
- 3.3 Lagen om parallellogram
- 4 rektangel
- 4.1 Diagonaler av en rektangel
- 5 kvadrat
- 6 Rhombus
- 7 Exempel
- 7.1 Exempel 1
- 7.2 Exempel 2
- 7.3 Exempel 3
- 8 Övningar lösta
- 8.1 - Övning 1
- 8.2 - Övning 2
- 9 Referenser
Fyrkantig klassificering
Enligt de motsatta sidornas parallellitet klassificeras fyrkantarna enligt följande:
- Trapes, när det inte finns någon parallellitet och fyrsidan är konvex.
- Trapets, när det finns parallellitet mellan ett enda par motsatta sidor.
- Parallellogram, när dess motsatta sidor är parallella två och två.
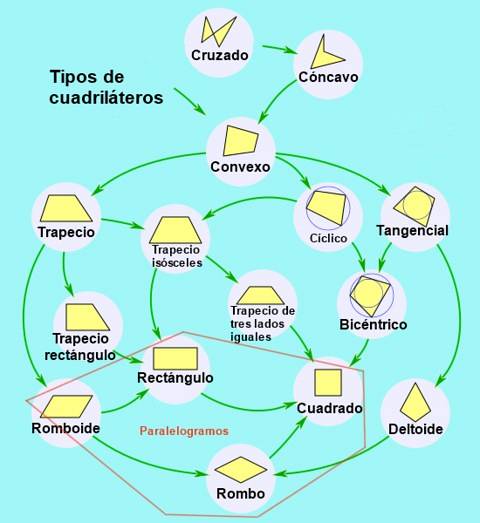
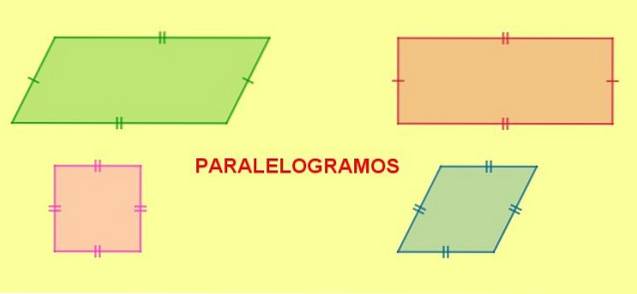
Typer av parallellogram
I sin tur kan parallellogram klassificeras enligt deras vinklar och sidor enligt följande:
- Rektangel, är parallellogrammet som har sina fyra inre vinklar med samma mått. De inre vinklarna i en rektangel bildar en rät vinkel (90º).
- Fyrkant, är en rektangel med sina fyra sidor lika stora.
- Diamant, är parallellogrammet med sina fyra lika sidor, men olika intilliggande vinklar.
- Romboid, parallellogram med olika intilliggande vinklar.
Trapets
Trapesformen är en konvex fyrkant med två parallella sidor.
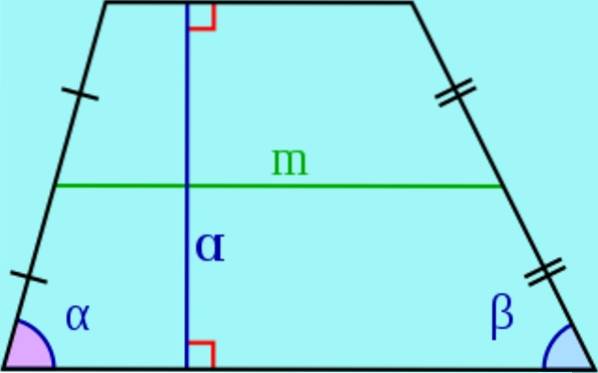
- I en trapetsform kallas de parallella sidorna baser och de icke-parallellerna kallas lateral.
- De höjd av en trapets är avståndet mellan de två baserna, det vill säga längden på ett segment med ändar vid baserna och vinkelrätt mot dem. Detta segment kallas också en trapetshöjd..
- De median är det segment som förenar mittpunkterna för sidorna. Det kan visas att medianen är parallell med trapesens baser och dess längd är lika med halvsumman av baserna.
- Området för en trapets är dess höjd multiplicerat med halvsumman av baserna:
Trapesens yta = höjd * (bas 1 + bas 2) / 2
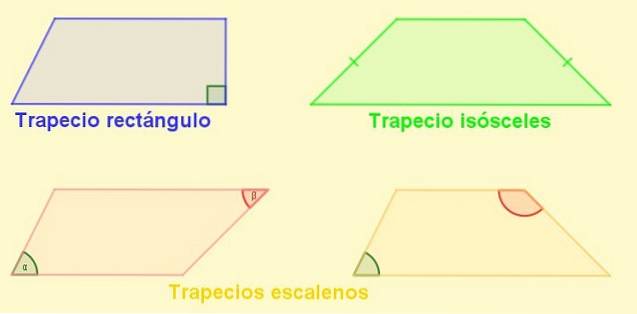
Typer av trapets
-Rektangel trapes: Är den med en lateral vinkelrät mot baserna. Denna laterala är också trapesens höjd.
-Trapezium likbenade: Den med lika långa sidor. I en likbent trapes är vinklarna intill baserna lika.
-Scalene trapets: Den med dess sidor av olika längd. Dess motsatta vinklar kan vara den ena och den andra stum, men det kan också hända att båda är stumpa eller båda är akuta..
Parallellogram
Parallellogrammet är en fyrkant, vars motsatta sidor är parallella två och två. I ett parallellogram är de motsatta vinklarna lika och de intilliggande vinklarna är kompletterande, eller med andra ord, de intilliggande vinklarna uppgår till 180º.
Om ett parallellogram har en rätt vinkel kommer alla andra vinklar att vara det, och den resulterande figuren kallas rektangel. Men om rektangeln också har sina intilliggande sidor av samma längd, är alla dess sidor lika och den resulterande figuren är a fyrkant.
När ett parallellogram har två intilliggande sidor av samma längd kommer alla dess sidor att ha samma längd och den resulterande figuren är a diamant-.
Höjden på ett parallellogram är ett segment med ändar på motsatta sidor och vinkelrätt mot dem..
Område för ett parallellogram
Arealet av ett parallellogram är produkten av basen gånger dess höjd, basen är en sida vinkelrät mot höjden (figur 6).
Areal för ett parallellogram = bas x höjd = a. h
Diagonaler av ett parallellogram
Kvadraten på diagonalen som börjar från en topp är lika med summan av kvadraterna på de två sidorna intill toppunkten plus den dubbla produkten från dessa sidor med cosinus för vinkeln för det toppunktet:
Ftvå = atvå + dtvå + 2 a d Cos (a)
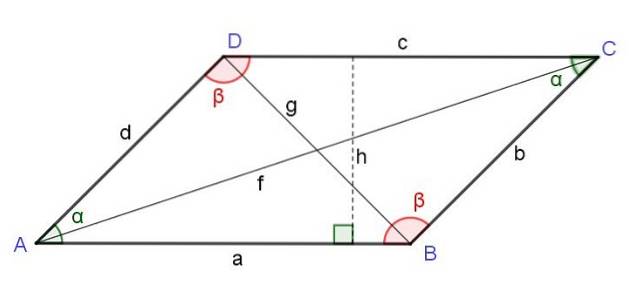
Kvadraten på diagonalen mittemot toppunkten för ett parallellogram är lika med summan av kvadraterna på de två sidorna intill nämnda toppunkt och subtraherar dubbelprodukten av dessa sidor med cosinus för vinkeln för det toppunktet:
gtvå = atvå + dtvå - 2 a d Cos (a)
Lagen om parallellogram
I varje parallellogram är summan av kvadraterna på dess sidor lika med summan av kvadraten på diagonalerna:
tilltvå + btvå + ctvå + dtvå = ftvå + gtvå
Resnurra
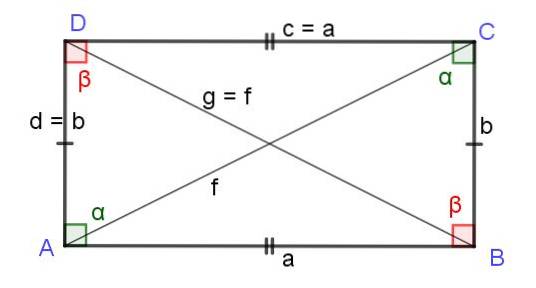
Rektangeln är en fyrkant med dess motsatta sidor parallella två och två och som också har en rät vinkel. Med andra ord är rektangeln en typ av parallellogram med rät vinkel. För att vara parallellogram, rektangeln har motsatta sidor av lika längd a = c och b = d.
Men som i varje parallellogram är de intilliggande vinklarna kompletterande och de motsatta vinklarna lika, i rektangeln eftersom den har en rätt vinkel, kommer den nödvändigtvis att bilda rät vinklar i de andra tre vinklarna. Nämligen i en rektangel mäter alla inre vinklar 90º eller π / 2 radianer.
Diagonaler av en rektangel
I en rektangel är diagonalerna lika långa, som kommer att visas nedan. Resonemanget är följande: En rektangel är ett parallellogram med alla sina rätta vinklar och ärver därför alla egenskaper hos parallellogrammet, inklusive formeln som ger längden på diagonalerna:
Ftvå = atvå+ dtvå + 2 a d Cos (a)
gtvå = atvå + dtvå - 2 a d Cos (a)
med α = 90º
Vad Cos (90º) = 0, då händer det att:
Ftvå = gtvå = atvå + dtvå
Det är f = g, och därför längderna F Y g av de två diagonalerna i rektangeln är lika och deras längd ges av:
Diagonaler längd på en rektangel = √ (atvå + btvå)
Även om det är i en rektangel med intilliggande sidor till Y b ena sidan tas som bas, den andra sidan kommer att vara höjd och följaktligen kommer rektangelns yta att vara:
Rektangelns yta = a x b.
Omkretsen är summan av alla sidor av rektangeln, men eftersom motsatserna är lika, följer det att för en rektangel med sidor till Y b omkretsen ges med följande formel:
Rektangelns omkrets = 2 (a + b)
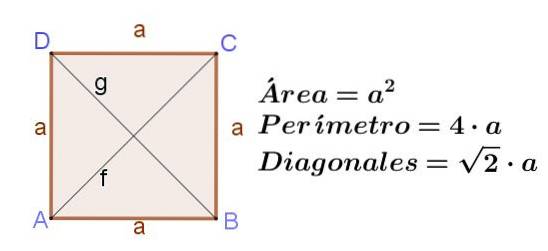
Fyrkant
Rutan är en rektangel med dess intilliggande sidor av samma längd. Om torget har en sida till, sedan dess diagonaler F Y g har samma längd, vilket är f = g = (√2) a.
Området för en kvadrat är dess sida kvadrat:
Area av en kvadrat = atvå
Rutan på en kvadrat är dubbelt så lång:
Kvadratens omkrets = 4 a
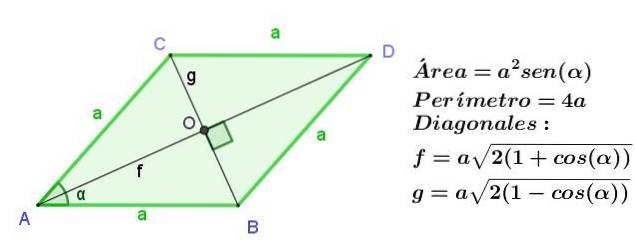
Diamant
Romben är ett parallellogram med dess intilliggande sidor av samma längd, men som i ett parallellogram är de motsatta sidorna lika då, alla sidor av en romb är lika långa.
Diagonalerna på en romb har olika längd men skär varandra i rät vinkel.
Exempel
Exempel 1
Visa att de fyrkantiga (inte korsade) de inre vinklarna uppgår till 360º.
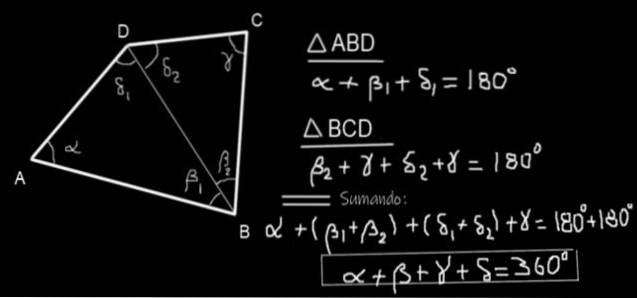
En fyrsidig ABCD övervägs (se figur 10) och den diagonala BD ritas. Två trianglar ABD och BCD bildas. Summan av de inre vinklarna för triangel ABD är:
a + p1 + 51 = 180º
Och summan av de inre vinklarna i triangeln BCD är:
β2 + y + δtvå = 180º
Lägga till de två ekvationerna vi får:
a + p1 + 51 + βtvå + y + δtvå = 180º + 180º
Gruppering:
a + (p1 + βtvå) + (51 + 5två) + γ = 2 * 180 °
Genom att gruppera och byta namn visas det äntligen att:
α + β + δ + γ = 360 °
Exempel 2
Visa att medianen för en trapets är parallell med dess baser och dess längd är semisumman av baserna.
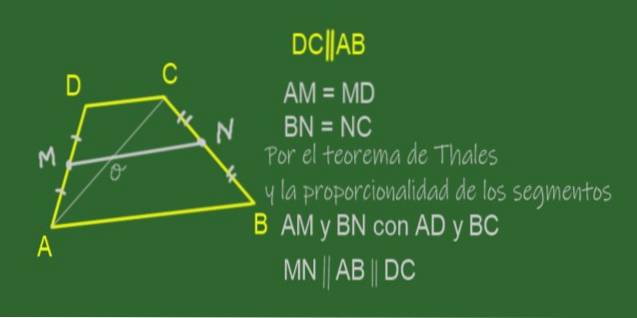
Medianen för en trapets är det segment som förenar mittpunkterna på dess sidor, det vill säga de icke-parallella sidorna. I den trapetsformade ABCD som visas i figur 11 är medianen MN.
Eftersom M är mittpunkten för AD och N är mittpunkten för BC är det sant att förhållandena AM / AD och BN / BC är lika.
Det vill säga AM är proportionellt mot BN i samma proportion som AD är mot BC, så villkoren ges för tillämpningen av Thales (ömsesidiga) sats som säger följande:
"Om proportionella segment bestäms i tre eller flera linjer skurna av två sekanter, är dessa linjer alla parallella".
I vårt fall dras slutsatsen att linjerna MN, AB och DC är parallella med varandra, därför:
"Len trapetsformats median är parallell med dess baser".
Nu kommer Thales-satsen att tillämpas:
"En uppsättning paralleller som klipps av två eller flera sekanter bestämmer proportionella segment".
I vårt fall AD = 2 AM, AC = 2 AO, så triangeln DAC liknar triangeln MAO, och följaktligen DC = 2 MO.
Ett liknande argument tillåter oss att bekräfta att CAB liknar CON, där CA = 2 CO och CB = 2 CN. Det följer omedelbart att AB = 2 PÅ.
Kort sagt, AB = 2 ON och DC = 2 MO. Så när vi lägger till har vi:
AB + DC = 2 PÅ + 2 MO = 2 (MO + PÅ) = 2 MN
Slutligen rensas MN:
MN = (AB + DC) / 2
Och det dras slutsatsen att medianen för en trapezoid mäter halvsummen av baserna, eller med andra ord: medianen mäter summan av baserna, dividerat med två.
Exempel 3
Visa att diagonalerna i en romb skär varandra i rät vinkel.

Tavlan i figur 12 visar den nödvändiga konstruktionen. Först ritas parallellogrammet ABCD med AB = BC, det vill säga en romb. Diagonalerna AC och DB bestämmer åtta vinklar som visas i figuren.
Med satsen (a.i.p.) som säger att alternerande inre vinklar mellan paralleller som skärs av en sekant bestämmer lika vinklar, kan vi fastställa följande:
a1 = γ1, a2 = y2, 51 = Β1 och 52 = P2. (*)
Å andra sidan, eftersom de intilliggande sidorna av en romb har samma längd, bestäms fyra likbeniga trianglar:
DAB, BCD, CDA och ABC
Nu åberopas triangelns (likbenade) sats, som säger att vinklarna intill basen är lika stora, varifrån man drar slutsatsen att:
51 = β2, δ2 = β1, α2 = γ1 och a1 = γ2 (**)
Om relationerna (*) och (**) kombineras, uppnås följande vinkeljämlikhet:
a1 = α2 = γ1 = γ1 å ena sidan och β1 = Β2 = δ1 = δ2 å andra sidan.
Påminner om samma triangelsats som säger att två trianglar med en lika sida mellan två lika vinklar är lika, har vi:
AOD = AOB och följaktligen också vinklarna ∡AOD = ∡AOB.
Då ∡AOD + ∡AOB = 180º, men eftersom båda vinklarna är lika stora, har vi 2 ∡AOD = 180º vilket innebär att ∡AOD = 90º.
Det vill säga det visas geometriskt att diagonalerna på en romb skär varandra i rät vinkel.
Övningar lösta
- Övning 1
Visa att de rätta vinklarna är kompletterande i en rätt trapets.
Lösning
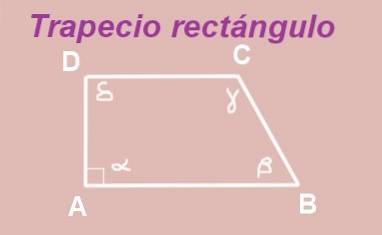
Trapezoid ABCD är konstruerad med baserna AB och DC parallella. Den inre vinkeln för toppunkt A är rätt (den mäter 90º), så vi har en rätt trapets.
Vinklarna α och δ är inre vinklar mellan två paralleller AB och DC, därför är de lika, det vill säga δ = α = 90º.
Å andra sidan har det visat sig att summan av de fyra vinklarnas inre vinklar uppgår till 360 °, det vill säga:
α + β + γ + δ = 90º + β + 90º + δ = 360º.
Ovanstående leder till:
β + δ = 180º
Bekräftar vad som ville visas, att vinklarna β och δ är kompletterande.
- Övning 2
Ett parallellogram ABCD har AB = 2 cm och AD = 1 cm, dessutom är vinkeln BAD 30º. Bestäm området för parallellogrammet och längden på dess två diagonaler.
Lösning
Området för ett parallellogram är produkten av basens längd gånger dess höjd. I detta fall tas längden på segmentet b = AB = 2 cm som grund, den andra sidan har längden a = AD = 1 cm och höjden h beräknas enligt följande:
h = AD * Sen (30º) = 1 cm * (1/2) = ½ cm.
Så: Area = b * h = 2 cm * ½ cm = 1 cmtvå.
Referenser
- C. E. A. (2003). Element av geometri: med övningar och kompassens geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Upptäck polygoner. Benchmark Education Company.
- Hendrik, V. (2013). Allmänna polygoner. Birkhäuser.
- IGER. (s.f.). Matematik första terminen Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren och Hornsby. (2006). Mathematics: Reasoning And Applications (tionde upplagan). Pearson Education.
- Patiño, M. (2006). Matematik 5. Redaktionellt program.
- Wikipedia. Fyrkantiga. Återställd från: es.wikipedia.com
Ingen har kommenterat den här artikeln än.