
Vilka är viktlagarna för kemi? (Exempel)
De viktlagar för kemi De är de som har visat att massorna av ämnena som reagerar inte gör det godtyckligt eller slumpmässigt; men genom att upprätthålla en konstant matematisk andel av heltal eller submultiplar därav, där elementens atomer varken skapas eller förstörs.
Tidigare har det krävts extraordinära resonemang för att upprätta dessa lagar. för även om det verkar för uppenbart nu, innan atom- eller molekylmassorna av elementen respektive föreningarna inte ens var kända.

Eftersom det inte var känt exakt hur mycket en mol atomer av varje element motsvarade, var kemister på 1700- och 1800-talet tvungna att förlita sig på de reagerande massorna. Så rudimentära analytiska balanser (toppbild) var oskiljaktiga följeslagare under hundratals experiment som krävdes för att fastställa viktlagarna..
Det är av den anledningen att när du studerar dessa kemilagar stöter du på massmätningar i varje ögonblick. Tack vare detta, extrapolera resultaten av experimenten, upptäcktes det att de kemiska föreningarna cigarrer bildas alltid med samma massandel av deras beståndsdelar.
Artikelindex
- 1 Lag om bevarande av massa
- 1.1 -Lavoisier experiment
- 1.2 -Balans av ekvationer
- 1.3 -Beräkningar
- 2 Lag med bestämda proportioner
- 2.1 -Illustration av lagen
- 2.2 -Applikationer
- 2.3 -Beräkningar
- 3 Lagen med flera proportioner eller Daltons lag
- 3.1 -Beräkningar
- 4 Lag om ömsesidiga proportioner
- 4.1-Exempel
- 5 Referenser
Lag om bevarande av massa
Denna lag säger att i en kemisk reaktion är reaktanternas totala massa lika med produktens totala massa; så länge systemet som beaktas är stängt och det finns inget utbyte av massa och energi med omgivningen.
I en kemisk reaktion försvinner inte ämnen utan omvandlas till andra ämnen av samma massa; därav den berömda frasen: "ingenting skapas, inget förstörs, allt förvandlas".
Historiskt föreslogs lagen om bevarande av massa i en kemisk reaktion först 1756 av Mikhail Lomonsov, som visade resultaten av sina experiment i sin tidskrift..
Senare 1774 presenterade Antoine Levoisier, fransk kemist, resultaten av sina experiment som gjorde det möjligt att fastställa detta; som, vissa också kallar det Lavoisiers lag.
-Lavoisier-experiment
På Lavoisiers tid (1743-1794) fanns Phlogiston-teorin, enligt vilken kroppar hade förmågan att ta eld eller brinna. Lavoisiers experiment gjorde det möjligt att kasta bort denna teori.
Lavoisier genomförde ett flertal metallförbränningsexperiment. Han vägde noggrant materialet före och efter förbränningen i en sluten behållare och fann att det var en uppenbar viktökning..
Men Lavoiser, baserat på sin kunskap om syrgasens roll i förbränningen, drog slutsatsen att viktökning vid förbränning berodde på att syre införlivades i det brinnande materialet. Begreppet metalloxider föddes.
Därför förblev summan av massorna av metaller som utsattes för förbränning och syre oförändrad. Denna slutsats möjliggjorde upprättandet av lagen om bevarande av massa.
-Ekvationsbalansering
Lagen om konservering av massor fastställde behovet av att balansera kemiska ekvationer, vilket garanterar att antalet alla element som deltar i en kemisk reaktion, både som reaktanter eller som produkter, är exakt samma..
Detta är ett väsentligt krav för noggrannheten i de stökiometriska beräkningarna som ska utföras..
-Beräkningar
Vattenmullar
Hur många mol vatten kan produceras vid förbränning av 5 mol metan i överskott av syre? Visa också att lagen om bevarande av materia är uppfylld..
CH4 + 2 Otvå => COtvå + 2 timmartvåELLER
Med beaktande av den balanserade ekvationen i reaktionen dras slutsatsen att 1 mol metan producerar 2 mol vatten.
Problemet kan lösas direkt med ett enkelt tillvägagångssätt, eftersom vi inte har 1 mol utan 5 mol CH4:
Mol vatten = 5 mol CH4(2 mol HtvåO / 1 mol CH4)
= 10
Vilket skulle motsvara 180 g HtvåO. Bildades också 5 mol eller 220 g COtvå, vilket är lika med en total massa på 400 g produkter.
För att lagen om bevarande av materia ska kunna uppfyllas måste 400 g reagens reagera; inte mer inte mindre. Av dessa 400 g motsvarar 80 g 5 mol CH4 (multipliceras med dess molekylvikt på 16 g / mol) och 320 g vid 10 mol Otvå (på samma sätt för sin molekylvikt på 32 g / mol).
Förbränning av ett magnesiumband
Ett 1,50 g magnesiumband brändes i en sluten behållare innehållande 0,80 g syre. Efter förbränning förblev 0,25 g syre i behållaren. a) Vilken massa syre reagerade? b) Hur mycket magnesiumoxid som bildades?
Massan av syre som reagerade erhålls med en enkel skillnad.
Förbrukad syrgasmassa = (initialmassa - restmassa) syre
= 0,80 g - 0,25 g
= 0,55 g Otvå (till)
Enligt lagen om bevarande av massa,
Massa av magnesiumoxid = massa av magnesium + massa av syre
= 1,50 g + 0,55 g
= 2,05 g MgO (b)
Lag med bestämda proportioner
Joseph Louis Proust (1754-1826), fransk kemist, insåg att i en kemisk reaktion reagerar de kemiska elementen alltid i fasta proportioner av massor för att bilda en förening ren specifik; därför är dess sammansättning konstant, oavsett källa eller ursprung, eller hur den syntetiseras.
Proust 1799 förklarade lagen med bestämda proportioner, som säger att: "När två eller flera element kombineras för att bilda en förening, gör de det i ett fast massförhållande." Därefter är detta förhållande fast och beror inte på den strategi som följts för beredningen av föreningen..
Denna lag är också känd som lagen om konstant sammansättning, som säger att: "Varje kemisk förening i ett renhetstillstånd innehåller alltid samma grundämnen, i en konstant andel av massan.".
-Lag illustration
Järn (Fe) reagerar med svavel (S) för att bilda järnsulfid (FeS), tre situationer kan noteras (1, 2 och 3):
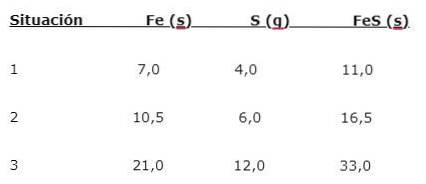
För att hitta den andel där elementen kombineras, dela den större massan (Fe) med den mindre massan (S). Beräkningen ger ett förhållande på 1,75: 1. Detta värde upprepas under de tre angivna villkoren (1, 2 och 3), där samma andel erhålls även om olika massor används..
Det vill säga 1,75 g Fe kombineras med 1,0 g S för att ge 2,75 g FeS.
-Applikationer
Genom att tillämpa denna lag är det möjligt att veta exakt massorna av elementen som måste kombineras för att erhålla en önskad massa av en förening..
På detta sätt kan information erhållas om överflödig massa av något av elementen som är involverade i en kemisk reaktion, eller om det finns ett begränsande reagens i reaktionen..
Dessutom appliceras den för att känna till en förenings centesimala sammansättning, och baserat på den senare kan formeln för en förening fastställas.
Centesimal sammansättning av en förening
Koldioxid (COtvå) bildades i följande reaktion:
C + Otvå => COtvå
12 g kol kombinerar 32 g syre för att ge 44 g koldioxid.
Så andelen kol är lika
Kolprocent = (12 g / 44 g) 100%
= 27,3%
Syreprocent = (32 g / 44 g) 100%
Andel syre = 72,7%
Med hjälp av uttalandet från lagen om konstant sammansättning kan det noteras att koldioxid alltid består av 27,3% kol och 72,7% syre.
-Beräkningar
Svaveltrioxid
När 4 g och 6 g svavel (S) reagerades med syre (O) i olika kärl, 10 g och 15 g svaveltrioxid (SO3).
Varför erhölls sådana mängder svaveltrioxid och inte andra?
Beräkna också mängden svavel som krävs för att kombinera med 36 g syre och den erhållna massan av svaveltrioxid.
Del A)
I den första behållaren blandas svavel med X g syre för att erhålla 10 g trioxid. Om lagen om bevarande av massa tillämpas kan vi lösa den syremassa som kombineras med svavlet.
Massa av syre = 10 g syretrioxid - 4 g svavel.
= 6 g
I behållare 2 blandas 6 g svavel med X g syre för att erhålla 15 svaveltrioxid.
Massa syre = 15 g svaveltrioxid - 6 g svavel
= 9 g
Vi fortsätter sedan med att beräkna O / S-förhållandena för varje container:
O / S-förhållande i situation 1 = 6 g O / 4 g S
= 1,5 / 1
O / S-förhållande i situation 2 = 9 g O / 6 g S
= 1,5 / 1
Vilket är i enlighet med vad som anges i lagen om definierade proportioner, vilket indikerar att elementen alltid kombineras i samma proportion för att bilda en viss förening..
Därför är de erhållna värdena korrekta och de som motsvarar tillämpningen av lagen.
Del b)
I föregående avsnitt beräknades ett värde på 1,5 / 1 för O / S-förhållandet.
g svavel = 36 syre (1 g svavel / 1,5 g syre)
= 24 g
g svaveltrioxid = 36 g syre + 24 g svavel
= 60 g
Klor och magnesium
Klor och magnesium kombineras i förhållandet 2,95 g klor för varje g magnesium. a) Bestäm de massor klor och magnesium som är nödvändiga för att erhålla 25 g magnesiumklorid. b) Hur stor är procentandelen av magnesiumklorid?
Del A)
Baserat på värdet 2,95 för Cl: Mg-förhållandet kan följande tillvägagångssätt göras:
2,95 g Cl + 1 g Mg => 3,95 g MgCltvå
Senare:
g Cl = 25 g MgCltvå (2,95 g Cl / 3,95 g MgCltvå)
= 18,67
g Mg = 25 g MgCltvå (1 g Mg / 3,95 g MgCltvå)
= 6,33
Så 18,67 g klor kombineras med 6,33 g magnesium för att producera 25 g magnesiumklorid..
Del b)
Beräkna först molekylmassan av magnesiumklorid, MgCltvå:
Molekylvikt MgCltvå = 24,3 g / mol + (2 35,5 g / mol)
= 95,3 g / mol
Magnesiumprocent = (24,3 g / 95,3 g) x 100%
= 25,5%
Klorprocent = (71 g / 95,3 g) x 100%
= 74,5%
Lag med flera proportioner eller Daltons lag
Lagen förklarades 1803 av den franska kemisten och meteorologen John Dalton, baserat på hans observationer angående reaktionerna från atmosfäriska gaser..
Lagen angavs på följande sätt: "När element kombineras för att ge mer än en förening, förenas en variabel massa av en av dem till en fast massa av den andra och den första har som en relation av kanoniska och otydliga tal".
Också: "När två element kombineras för att skapa olika föreningar, givet en fast mängd av en av dem, är de olika mängderna av det andra elementet som kombineras med nämnda fasta mängd för att producera föreningarna, i relation till enkla heltal".
John Dalton gjorde den första moderna beskrivningen av atomen som en komponent i de kemiska elementen, när han påpekade att grundämnena består av odelbara partiklar som kallas atomer..
Dessutom postulerade han att föreningar bildas när atomer med olika element kombineras med varandra i enkla heltal..
Dalton slutförde Prousts undersökningsarbeten. Han påpekade förekomsten av två tennoxider, med procent på 88,1% och 78,7% tenn med motsvarande procentandel syre, 11,9% respektive 21,3%..
-Beräkningar
Vatten och väteperoxid
Visa att föreningarna vatten, HtvåO och väteperoxid, HtvåELLERtvå, följa lagen om flera proportioner.
Elementens atomvikt: H = 1 g / mol och syre = 16 g / mol.
Molekylvikter för föreningar: HtvåO = 18 g / mol och HtvåELLERtvå = 34 g / mol.
Väte är grundämnet med en fast mängd i HtvåO och HtvåELLERtvå, så proportionerna mellan O och H i båda föreningarna kommer att fastställas.
O / H-förhållande i HtvåO = (16 g / mol) / (2 g / mol)
= 8/1
O / H-förhållande i HtvåELLERtvå = (32 g / mol) / (2 g / mol)
= 16/1
Förhållandet mellan båda proportionerna = (16/1) / (8/1)
= 2
Så O / H-förhållandet mellan väteperoxid och vatten är 2, ett enkelt heltal. Därför är överensstämmelse med lagen om flera proportioner visad..
Kväveoxider
Vilken syremassa som kombineras med 3,0 g kväve i a) kväveoxid, NO och b) kvävedioxid, NOtvå. Visa att NEJ och NEJtvå följa lagen om flera proportioner.
Massa av kväve = 3 g
Atomvikter: kväve, 14 g / mol och syre, 16 g / mol.
Beräkningar
I NO kombineras en N-atom med 1 O-atom, så syrgasmassan som kombineras med 3 g kväve kan beräknas enligt följande tillvägagångssätt:
g O = g kväve · (PA. O / PA. N)
= 3 g (16 g / mol / 14 g / mol)
= 3,43 g O
I NEJtvå, en N-atom kombineras med 2 O-atomer, så massan av syre som kombineras är:
g syre = 3 g (32 g / mol / 14 g / mol)
= 6,86 g O
O / N-förhållande i NO = 3,43 g O / 3 g N
= 1143
O / N-förhållande i NOtvå = 6,86 g O / 3 g N
= 2282
Värdet på sambandet mellan O / N-proportionerna = 2282/1143
= 2
Så värdet på O / N-förhållandet är 2, ett enkelt heltal. Därför uppfylls lagen om flera proportioner..
Ömsesidiga proportioner lag
Denna lag formulerad av Richter och Carl F. Wenzel separat, fastställer att massandelen av två föreningar med ett element gemensamt, gör det möjligt att bestämma andelen av en tredje förening bland de andra elementen om de reagerar.
Om du till exempel har de två föreningarna AB och CB kan du se att det gemensamma elementet är B.
Richter-Wenzel-lagen eller lagen om ömsesidiga proportioner säger att om vi vet hur mycket av A som reagerar med B för att ge AB, och hur mycket av C som reagerar med B för att ge CB, kan vi beräkna massan av A som behövs för att reagera med en massa av C för att bilda AC.
Och resultatet är att förhållandet A: C eller A / C måste vara en multipel eller delmultipel av A / B eller C / B. Denna lag uppfylls emellertid inte alltid, särskilt när elementen presenterar olika oxidationstillstånd..
Av alla underliga lagar är detta kanske den mest "abstrakta" eller komplicerade. Men om den analyseras ur en matematisk synvinkel kommer det att ses att den endast består av omvandlingsfaktorer och avbokningar.
-Exempel
Metan
Om det är känt att 12 g kol reagerar med 32 g syre för att bilda koldioxid; och att å andra sidan 2 g väte reagerar med 16 g syre för att bilda vatten, då kan massproportionerna C / O och H / O för CO uppskattastvå och HtvåEller, respektive.
Beräkning av C / O och H / O har vi:
C / O = 12 g C / 32 g O
= 3/8
H / O = 2 g H / 16 g O
= 1/8
Syre är det vanliga elementet, och du vill veta hur mycket kol som reagerar med väte för att producera metan; det vill säga du vill beräkna C / H (eller H / C). Sedan är det nödvändigt att göra en uppdelning av de tidigare proportionerna för att visa om ömsesidighet uppfylls eller inte:
C / H = (C / O) / (H / O)
Observera att på detta sätt annulleras O: erna och C / H förblir:
C / H = (3/8) / (1/8)
= 3
Och 3 är en multipel av 3/8 (3/8 x 8). Detta innebär att 3 g C reagerar med 1 g H för att ge metan. Men för att kunna jämföra det med COtvå, multiplicera C / H med 4, vilket är lika med 12; detta ger 12 g C som reagerar med 4 g H för att bilda metan, vilket också är sant.
Magnesiumsulfid
Om det är känt att 24 g magnesium reagerar med 2 g väte för att bilda magnesiumhydrid; och att dessutom 32 g svavel reagerar med 2 g väte för att bilda vätesulfid, elementet gemensamt är väte och vi vill beräkna Mg / S från Mg / H och H / S.
Sedan, när vi beräknar Mg / H och H / S separat, har vi:
Mg / H = 24 g Mg / 2 g H
= 12
H / S = 2 g H / 32 g S
= 1/16
Det är dock bekvämt att använda S / H för att avbryta H. Därför är S / H lika med 16. När detta är gjort fortsätter vi med att beräkna Mg / S:
Mg / S = (Mg / H) / (S / H)
= (12/16)
= 3/4
Och 3/4 är en delmultipel på 12 (3/4 x 16). Mg / S-förhållandet indikerar att 3 g Mg reagerar med 4 g svavel för att bilda magnesiumsulfid. Du måste dock multiplicera Mg / S med 8 för att kunna jämföra det med Mg / H. Således reagerar 24 g Mg med 32 g svavel för att ge denna metallsulfid.
Aluminiumklorid
Det är känt att 35,5 g Cl reagerar med 1 g H för att bilda HCl. På samma sätt reagerar 27 g Al med 3 g H för att bilda AlH3. Beräkna andelen aluminiumklorid och berätta om en sådan förening följer Richter-Wenzels lag.
Återigen fortsätter vi med att beräkna Cl / H och Al / H separat:
Cl / H = 35,5 g Cl / 1 g H
= 35,5
Al / H = 27 g Al / 3 g H
= 9
Nu beräknas Al / Cl:
Al / Cl = (Al / H) / (Cl / H)
= 9 / 35,5
≈ 0.250 eller 1/4 (faktiskt 0.253)
Det vill säga 0,250 g Al reagerar med 1 g Cl för att bilda motsvarande salt. Men återigen måste Al / Cl multipliceras med ett tal som gör att det kan jämföras (för enkelhets skull) med Al / H.
Beräkningsfelaktigheter
Al / Cl multipliceras sedan med 108 (27 / 0.250), vilket ger 27 g Al som reagerar med 108 g Cl. Detta är inte exakt fallet. Om vi till exempel tar värdet 0,253 gånger Al / Cl och multiplicerar det med 106,7 (27 / 0,253), kommer vi att ha 27 g Al reagerar med 106,7 g Cl; som är närmare verkligheten (AlCl3, med en PA av 35,5 g / mol för Cl).
Här är hur Richters lag kan börja vackla på grund av precision och missbruk av decimaler..
Referenser
- Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan). CENGAGE Learning.
- Flores, J. Química (2002). Redaktionellt Santillana.
- Joaquín San Frutos Fernández. (s.f.). De underliga och volymetriska lagarna. Återställd från: encina.pntic.mec.es
- Toppr. (s.f.). Lagar om kemisk kombination. Återställd från: toppr.com
- Lysande. (2019). Lagar om kemisk kombination. Återställd från: brilliant.org
- Kemi LibreTexts. (2015, 15 juli). Grundläggande kemiska lagar. Återställd från: chem.libretexts.org
- Helmenstine, Anne Marie, Ph.D. (18 januari 2019). Lag om bevarande av massa. Återställd från: thoughtco.com


Ingen har kommenterat den här artikeln än.