Vilka delar är det kartesiska planet?

De delar av det kartesiska planet De består av två riktiga linjer, vinkelräta, som delar det kartesiska planet i fyra regioner. Var och en av dessa regioner kallas kvadranter och elementen i det kartesiska planet kallas punkter. Planet, tillsammans med koordinataxlarna, anropas Kartesiskt plan till ära för den franska filosofen René Descartes, som uppfann analytisk geometri.

De två linjerna (eller koordinataxlarna) är vinkelräta eftersom de bildar en vinkel på 90 ° mellan dem och de skär varandra vid en gemensam punkt (ursprung). En av linjerna är horisontell, kallas ursprunget för x (eller abscissa) och den andra linjen är vertikal, kallas ursprunget för y (eller ordinat).

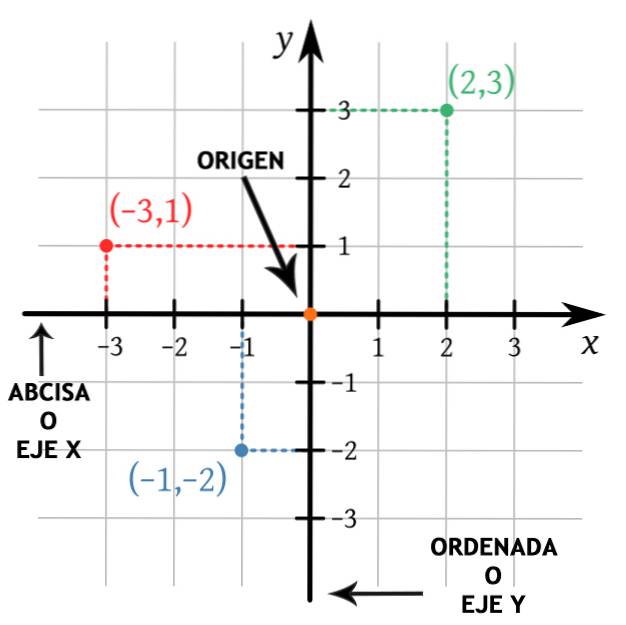
Den positiva halvan av X-axeln är till höger om ursprunget och den positiva halvan av Y-axeln är upp från ursprunget. Detta gör det möjligt att skilja de fyra kvadranterna i det kartesiska planet, vilket är mycket användbart när man plottar punkter i planet..

Poäng på det kartesiska planet

Vid varje punkt P planet kan tilldelas ett par verkliga nummer som är dess kartesiska koordinater.

Om en horisontell linje och en vertikal linje passerar igenom P, och dessa skär X-axeln och Y-axeln vid punkterna till Y b respektive koordinaterna för P Dom är (till,b). Det kallas (till,b) ett ordnat par och den ordning i vilken siffrorna skrivs är viktig.

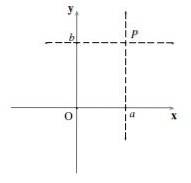
Det första numret, till, är koordinaten i "x" (eller abscissa) och det andra numret, b, är y-koordinaten (eller ordinaten). Notationen används P = (till,b).

Det framgår av det sätt på vilket det kartesiska planet konstruerades att ursprunget motsvarar koordinaterna 0 på "x" -axeln och 0 på "y" -axeln, det vill säga, ELLER= (0,0).

Kvadrater av det kartesiska planet

Som kan ses i de föregående figurerna genererar koordinataxlarna fyra olika regioner som är kvadranterna för det kartesiska planet, vilka betecknas med bokstäverna I, II, III Y IV och dessa skiljer sig från varandra i tecknet som finns i punkterna i var och en av dem.

Kvadrant Jag

Kvadrantens punkter Jag är de som har båda koordinaterna med ett positivt tecken, det vill säga deras x-koordinat och y-koordinat är positiva.

Till exempel poängen P = (2,8). För att rita den är punkt 2 placerad på "x" -axeln och punkt 8 på "y" -axeln, sedan ritas de vertikala respektive horisontella linjerna och där de skär var där punkten är. P.

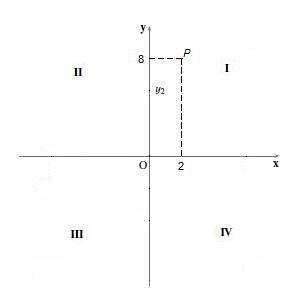
Kvadrant II

Kvadrantens punkter II de har en negativ "x" -koordinat och en positiv "y" -koordinat. Till exempel poängen Q = (- 4,5). Det ritas fram som i föregående fall.

Kvadrant III

I denna kvadrant är tecknet på båda koordinaterna negativt, det vill säga "x" -koordinaten och "y" -koordinaten är negativa. Till exempel är punkten R = (- 5, -2).

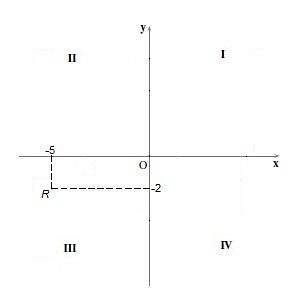
Kvadrant IV

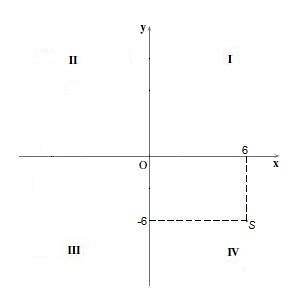
I kvadranten IV punkterna har en positiv "x" -koordinat och en negativ "y" -koordinat. Till exempel poängen S = (6, -6).

Referenser

1. Fleming, W., & Varberg, D. (1991). Algebra och trigonometri med analytisk geometri. Pearson Education.
2. Larson, R. (2010). Precalculus (8 utgåva). Cengage Learning.
3. Leal, J. M., & Viloria, N. G. (2005). Plans analytisk geometri. Mérida - Venezuela: Ledare Venezolana C. A.
4. Oteyza, E. (2005). Analytisk geometri (Andra upplagan). (G. T. Mendoza, red.) Pearson Education.
5. Oteyza, E. d., Osnaya, E. L., Garciadiego, C. H., Hoyo, A. M., & Flores, A. R. (2001). Analytisk geometri och trigonometri (Första upplagan). Pearson Education.
6. Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Beräkning (Nionde upplagan). Prentice hall.
7. Scott, C. A. (2009). Cartesian Plane Geometry, Part: Analytical Conics (1907) (omtryck ed.). Blixtkälla.