
Moody diagramekvationer, vad det är för, applikationer
De lynnig diagram består av en serie kurvor ritade på logaritmiskt papper, som används för att beräkna friktionsfaktorn som finns i flödet av en turbulent vätska genom en cirkulär kanal.
Med friktionsfaktor F friktionsenergiförlust utvärderas, ett viktigt värde för att bestämma korrekt prestanda för pumpar som distribuerar vätskor som vatten, bensin, råolja och andra.

För att känna till energin i flödet av en vätska är det nödvändigt att känna till vinsterna och förlusterna på grund av faktorer som hastighet, höjd, närvaron av enheter (pumpar och motorer), effekterna av vätskans viskositet och friktion mellan den. rörets väggar.
Artikelindex
- 1 Ekvationer för energin hos en vätska i rörelse
- 1.1 -Friktionsfaktor och Reynolds-nummer
- 2 Vad är det för?
- 3 Hur tillverkas den och hur används den??
- 3.1 - Fungerat exempel 1
- 4 applikationer
- 4.1 -Löst exempel 2
- 5 Referenser
Ekvationer för energin i en rörlig vätska
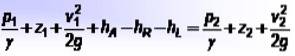
- sid1 Y sidtvå är trycket vid varje punkt,
- z1 Y ztvå är höjderna med avseende på referenspunkten,
- v1 Y vtvå är respektive fluidhastigheter,
- hTILL är den energi som pumparna tillför, hR är den energi som tas av någon anordning som en motor, och hL täcker vätskeenergiförluster på grund av friktion mellan vätska och rörväggar, liksom andra mindre förluster.
Värdet av hL beräknas med Darcy-Weisbach-ekvationen:
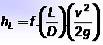
Var L är rörets längd, D är dess innerdiameter, v är vätskans hastighet och g är värdet på accelerationen på grund av tyngdkraften. Dimensionerna på hL är längd och vanligtvis är enheterna där den representeras meter eller fot.
-Friktionsfaktor och Reynolds-nummer
Att beräkna F empiriska ekvationer erhållna från experimentella data kan användas. Det är nödvändigt att skilja om det är en vätska i en laminär regim eller i en turbulent regim. För den laminära regimen F lätt utvärderad:
f = 64 / NR
Var NR är Reynolds-talet, vars värde beror på regimen där vätskan är. Kriterierna är:
Laminärt flöde: NR < 2000 el flujo es laminar; Flujo turbulento NR > 4000; Övergångsordning: 2000 < NR < 4000
Reynolds-numret (måttfritt) beror i sin tur på vätskans hastighet v, rörets innerdiameter D och kinematisk viskositet n av vätskan, vars värde erhålls med hjälp av tabeller:
NR = v.D / n
Colebrook ekvation
För ett turbulent flöde är den mest accepterade ekvationen i koppar- och glasrör Cyril Colebrook (1910-1997), men den har nackdelen att F det är inte uttryckligt:
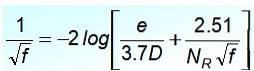
I denna ekvation kvoten e / D är rörets relativa grovhet och NR är Reynolds-numret. En noggrann iakttagelse visar att det inte är lätt att låta F till vänster om jämställdheten, så det är inte lämpligt för omedelbara beräkningar.
Colebrook själv föreslog detta tillvägagångssätt, som är uttryckligt, giltigt med vissa begränsningar:

Vad är det för?
Moody-diagrammet är användbart för att hitta friktionsfaktorn F ingår i Darcys ekvation, eftersom det i Colebrooks ekvation inte är lätt att uttrycka F direkt i termer av andra värden.
Dess användning förenklar att erhålla värdet av F, genom att innehålla den grafiska representationen av F i funktion av NR för olika värden av relativ ojämnhet i logaritmisk skala.
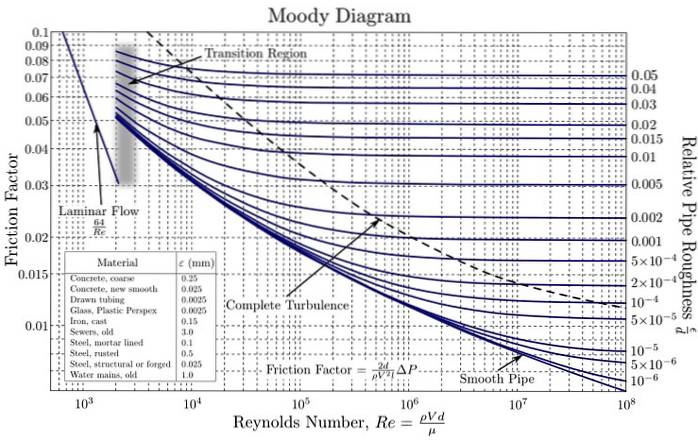
Dessa kurvor har skapats från experimentdata med olika material som vanligtvis används i rörtillverkning. Använd en logaritmisk skala för båda F som för NR det är nödvändigt, eftersom de täcker ett mycket brett spektrum av värden. På detta sätt underlättas kartläggningen av värden av olika storleksordningar..
Den första grafen för Colebrook-ekvationen erhölls av ingenjören Hunter Rouse (1906-1996) och strax efter att den modifierades av Lewis F. Moody (1880-1953) i den form som den används idag..
Den används för både cirkulära och icke-cirkulära rör, helt enkelt att ersätta den hydrauliska diametern för dessa.
Hur tillverkas det och hur används det??
Som förklarats ovan är Moody-diagrammet gjord av många experimentella data, presenterade i grafisk form. Här är stegen för att använda den:
- Beräkna Reynolds-nummer NR för att avgöra om flödet är laminärt eller turbulent.
- Beräkna den relativa grovheten med ekvationen ochr = e / D., var och är materialets absoluta ojämnhet och D är rörets innerdiameter. Dessa värden erhålls genom tabeller.
- Nu när du har det ochr Y NR, projicera vertikalt tills den når kurvan som motsvarar ochr erhållits.
- Projicera horisontellt och till vänster för att läsa värdet av F.
Ett exempel hjälper till att enkelt visualisera hur diagrammet används.
-Fungerat exempel 1
Bestäm friktionsfaktorn för vatten vid 160 ° F som flyter med en hastighet av 22 ft / s i en kanal tillverkad av obestruket smidesjärn med en innerdiameter på 1 tum..
Lösning
Nödvändiga data (finns i tabeller):
Kinematisk viskositet hos vatten vid 160ºF: 4,38 x 10-6 fottvå/ s
Absolut grovhet av obestruket smidesjärn: 1,5 x 10 -4 fötter
Första steget
Reynolds-talet beräknas, men inte innan den inre diametern passerar från 1 tum till fot:
1 tum = 0,0833 fot
NR = (22 x 0,0833) / 4,38 x 10-6= 4,18 x 10 5
Enligt de kriterier som visas tidigare är det ett turbulent flöde, då gör Moody-diagrammet det möjligt att erhålla motsvarande friktionsfaktor utan att behöva använda Colebrook-ekvationen.
Andra steg
Du måste hitta den relativa grovheten:
ochr = 1,5 x 10-4 / 0,0833 = 0,0018
Tredje steget
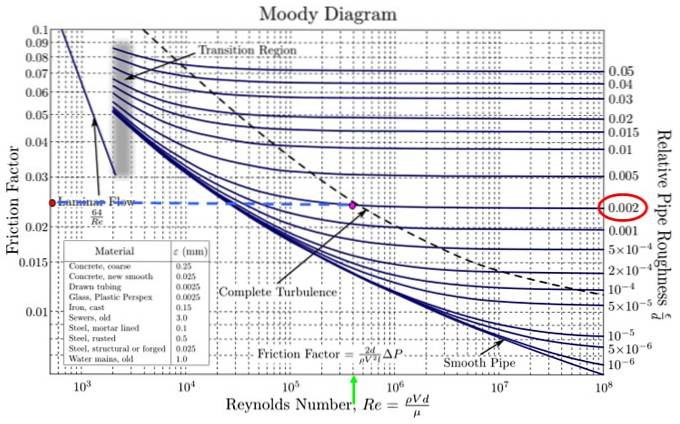
I det medföljande Moody-diagrammet är det nödvändigt att gå ytterst till höger och hitta den närmaste relativa råheten till det erhållna värdet. Det finns ingen som motsvarar exakt 0,0018 men det finns en som är ganska nära, den på 0,002 (röd oval i figuren).
Samtidigt söks motsvarande Reynolds-nummer på den horisontella axeln. Det närmaste värdet 4,18 x 10 5 är 4 x 10 5 (grön pil i figuren). Skärningspunkten för båda är fuchsia-punkten.
Fjärde steget
Projicera till vänster efter den blå prickade linjen och nå den orange punkten. Uppskatta nu värdet på F, med hänsyn till att delningarna inte är lika stora eftersom de är en logaritmisk skala på både den horisontella och vertikala axeln.
Moody-diagrammet i figuren har inte fina horisontella indelningar, därför är värdet på F i 0,024 (det är mellan 0,02 och 0,03 men det är inte hälften men lite mindre).
Det finns miniräknare online som använder Colebrook-ekvationen. En av dem (se referenser) gav värdet 0,023664639 för friktionsfaktorn.
Applikationer
Moody-diagrammet kan användas för att lösa tre typer av problem, förutsatt att vätskan och rörets absoluta ojämnhet är kända:
- Beräkning av tryckfallet eller tryckdifferensen mellan två punkter, förutsatt rörets längd, höjdskillnaden mellan de två punkterna som ska beaktas, hastigheten och rörets inre diameter.
- Bestämning av flödet, med kännedom om rörets längd och diameter, plus det specifika tryckfallet.
- Utvärdering av rörets diameter när längd, flöde och tryckfall mellan de punkter som ska beaktas är kända.
Problem av den första typen löses direkt med hjälp av diagrammet, medan de av den andra och tredje typen kräver användning av ett datorpaket. Till exempel, i den tredje typen, om rörets diameter inte är känd, kan Reynolds-talet inte utvärderas direkt, inte heller den relativa ojämnheten..
Ett sätt att lösa dem är att anta en initial inre diameter och därifrån successivt justera värdena för att erhålla det tryckfall som anges i problemet..
-Fungerat exempel 2
Du har 160 ° F vatten som strömmar stadigt längs ett 1-tums diameter obelagt smidesjärnsrör med en hastighet av 22 ft / s. Bestäm tryckdifferensen orsakad av friktion och pumpkraften som krävs för att bibehålla flödet i en längd av det horisontella röret L = 200 fot långt..
Lösning
Data som behövs: tyngdacceleration är 32 ft / stvå ; den specifika vikten av vatten vid 160ºF är γ = 61,0 lb-kraft / ft3
Detta är röret från löst exempel 1, därför är friktionsfaktorn redan känd F, vilket har uppskattats till 0,0024. Detta värde tas med i Darcy-ekvationen för att utvärdera friktionsförluster:

Den erforderliga pumpkraften är:
W = v. A. (s1 - sidtvå)
Där A är rörets tvärsnittsarea: A = p. (Dtvå/ 4) = s. (0,0833två/ 4) fottvå = 0,00545 fottvå
W = 22 fot / s. 2659,6 lb-kraft / fttvå. 0,00545 fottvå= 318,9 lb-kraft. fötter
Effekt uttrycks bäst i watt, för vilken omvandlingsfaktorn krävs:
1 Watt = 0.737 lb-kraft. fötter
Därför är effekten som krävs för att upprätthålla flödet W = 432,7 W
Referenser
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw Hill. 335- 342.
- Franzini, J. 1999. Fluid Mechanics with Application is in Engineering. Mc. Graw Hill. 176-177.
- LMNO Engineering. Moody Friction Factor Calculator. Återställd från: lmnoeng.com.
- Mott, R. 2006. Fluid Mechanics. 4: e. Utgåva. Pearson Education. 240-242.
- Ingenjörsverktygslådan. Moody Diagram. Återställd från: engineeringtoolbox.com
- Wikipedia. Moody Chart. Återställd från: en.wikipedia.org



Ingen har kommenterat den här artikeln än.